README.md
In haydo1117/pruin: Compute finite-time ruin probability via bivariate Laguerre series

pruin

The goal of pruin is to compute finite-time ruin probability via bivariate Laguerre series, see “Finite-time ruin probabilities using bivariate Laguerre series”. Currently support (1) combination of exponentials, (2) exponential, (3) generalised inverse Gaussian, (4) Normal truncated above zero, and (5) Weibull. For exponential distribution, Inverse Laplace Transform using Gaver-Stehfest algorithm is also included. As a by-product, a function to perform Inverse Laplace Transform is also included.

Note the bivariate Laguerre series method generally only works when the probability to be calculated is of reasonable size, i.e. cannot be too small. This is due to the precision limitations in R (where floating point numbers are of size 64), while huge precision is required for the method. While a change of scale may help, result is only credible when the top output from uscale_search are consistent with negligible error. For a serious calculation, computer programs with high precision arithmetic should be used. For example, current implemetation does not seem to work well for generalised inverse Gaussian with negative alpha parameter.

You can install the development version of pruin from GitHub with:

# install.packages("devtools")
devtools::install_github("haydo1117/pruin")

R version 4.1+ is required.

library(pruin)
library(polynom)
#> Warning: package 'polynom' was built under R version 4.1.2

Process parameters:

c <- 1.1
lambda <- 1

This section displays the use of the package for different claim distributions. It aims to recover some of the values in tables in the article “Finite-time ruin probabilities using bivariate Laguerre series”. Run ?FUNCTION_NAME for details of specific function.

Since uscale_search takes time, it is mostly commented out for this document. The specific chosen values of u_scale were determined using uscale_search. Uncomment those lines for full results.

Rate $\beta=1$ is used.

Inverse Laplace

Run ?ruin_prob_exp for details. n is the number of terms used in the Gaver-Stehfest algorithm. Large n results in divergence due to numerical precision issue. Small n does not converge.

ruin_prob_exp_gs(u=10,t=2,c,lambda,beta=1,plot=FALSE) # `plot=TRUE` for a visualisation
#>          n=1          n=2          n=3          n=4          n=5          n=6 
#> 9.354836e-03 5.883915e-05 1.192908e-03 1.344378e-03 1.350304e-03 1.350000e-03 
#>          n=7          n=8          n=9         n=10 
#> 1.349981e-03 1.349987e-03 1.349988e-03 1.349991e-03

# once `n` is chosen, switch off `try_n`
ruin_prob_exp_gs(u=10,t=2,c,lambda,beta=1,n=7,try_n=FALSE)
#> [1] 0.001349981

Bivariate Laguerre

exp_search <- uscale_search(u=10,t=2,c=c,lambda=lambda,family=exponential()(beta=1)) # search for u_scale
head(exp_search)
#>     u_scale         res           err
#> 1 0.5179475 0.001350093 -4.282286e-07
#> 2 0.5428675 0.001350092 -5.064892e-07
#> 3 0.4941713 0.001350084 -6.047761e-07
#> 4 0.5689866 0.001350077 -8.710763e-07
#> 5 0.4714866 0.001350026 -1.080568e-06
#> 6 0.5963623 0.001349991 -1.656331e-06

ruin_prob_ls(u=10,t=2,c,lambda,family=exponential()(beta=1),check=TRUE,u_scale = 0.6) # once u_scale is chosen
#> Maximum magnitude of eigen value of Q3 is 0.988350078157619 
#> Approximation error for psi(0,t=Inf) is -1.80084723744312e-06
#> [1] 0.001349969

ce1 <- comb_exponential()(w=c(2,-1),beta=c(1.5,3))
# uscale_search(u=10,t=2,c=1.1,lambda=1,family=ce1)
ruin_prob_ls(u=10,t=2,c=1.1,lambda=1,family=ce1,check=TRUE,u_scale = 1.0715193)
#> Maximum magnitude of eigen value of Q3 is 0.982386542356505 
#> Approximation error for psi(0,t=Inf) is -0.000106902542151399
#> [1] 0.0002601599

ce2 <- comb_exponential()(w=c(1/3,2/3),beta=c(0.5,2))
# uscale_search(u=10,t=2,c=1.1,lambda=1,family=ce2)
ruin_prob_ls(u=10,t=2,c=1.1,lambda=1,family=ce2,check=TRUE,u_scale = 0.6250552)
#> Maximum magnitude of eigen value of Q3 is 0.990030619800819 
#> Approximation error for psi(0,t=Inf) is 4.08372353940534e-05
#> [1] 0.008668747

w1 <- weibull()(alpha=2,beta=1/gamma(1+1/2))
# uscale_search(u=8,t=8,c=1.1,lambda=1,family=w1)
ruin_prob_ls(u=8,t=8,c=1.1,lambda=1,family=w1,check=TRUE,u_scale = 1.6982437)
#> Maximum magnitude of eigen value of Q3 is 0.974085350119468 
#> Approximation error for psi(0,t=Inf) is -0.000250509636899876
#> [1] 0.01551734

w2 <- weibull()(alpha=3,beta=1/gamma(1+1/3))
# uscale_search(u=4,t=4,c=1.1,lambda=1,family=w2)
ruin_prob_ls(u=4,t=4,c=1.1,lambda=1,family=w2,check=TRUE,u_scale = 3.0199517)
#> Maximum magnitude of eigen value of Q3 is 0.953023270944534 
#> Approximation error for psi(0,t=Inf) is 0.00619105609471005
#> [1] 0.05679952

g1 <- gig()(a=5.03251,b=0.01987,alpha=2.5)
# uscale_search(u=4,t=4,c=1.1,lambda=1,family=g1)
ruin_prob_ls(u=4,t=4,c=1.1,lambda=1,family=g1,check=TRUE,u_scale = 2.6302680)
#> Maximum magnitude of eigen value of Q3 is 0.957806304142554 
#> Approximation error for psi(0,t=Inf) is 0.00712739149898844
#> [1] 0.08464718

g2 <- gig()(a=0.32497,b=0.61543,alpha=-0.75)
gig_search <- uscale_search(u=4,t=4,c=1.1,lambda=1,family=g2) 
head(gig_search) # unstable ("err" too large)
#>     u_scale        res       err
#> 1 0.8286428  0.2035913 0.3969735
#> 2 1.0000000 -0.2020989 1.3652325
#> 3 1.0715193 -0.8892607 2.4536362
#> 4 1.0964782 -1.2325875 2.8444975
#> 5 0.9102982 -1.8274286 3.8461649
#> 6 1.0471285 -2.9014884 5.5015548

tn1 <- truncated_normal()(mu=0,sigma=sqrt(pi/2))
# uscale_search(u=8,t=6,c=1.1,lambda=1,family=tn1)
ruin_prob_ls(u=8,t=6,c=1.1,lambda=1,family=tn1,check=TRUE,u_scale = 1.1481536)
#> Maximum magnitude of eigen value of Q3 is 0.9816450385389 
#> Approximation error for psi(0,t=Inf) is 5.02053729289909e-05
#> [1] 0.01652747

tn_par <- 1/(1+dnorm(1)/(1-pnorm(-1)))
tn2 <- truncated_normal()(mu=tn_par,sigma=tn_par)
# uscale_search(u=6,t=4,c=1.1,lambda=1,family=tn2)
ruin_prob_ls(u=6,t=4,c=1.1,lambda=1,family=tn2,check=TRUE,u_scale = 1.4791084)
#> Maximum magnitude of eigen value of Q3 is 0.977158844750742 
#> Approximation error for psi(0,t=Inf) is -0.000440636302659336
#> [1] 0.01979806

# laplace transform of constant function k
Fconst <- function(x,k)k/x
fn_gs(Fconst,2,n=15,k=2,plot=FALSE)
#>        n=1        n=2        n=3        n=4        n=5        n=6        n=7 
#>   2.000000   2.000000   2.000000   2.000000   2.000000   2.000000   2.000000 
#>        n=8        n=9       n=10       n=11       n=12       n=13       n=14 
#>   2.000000   1.999999   2.000049   2.000179   2.047860   1.981037   3.410230 
#>       n=15 
#> 201.889947

For Weibull and truncated Normal (say 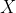$X$ with density $f_X$ ), the raw moments can be determined analytically in terms of gamma function (gamma() in R) for Weibull and Normal cumulative density function (pnorm() in R) for truncated Normal.

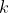Denote $x\mapsto L_k(x)=\sum_{j=0}^k l_j x^j$ the Laguerre polynomial or order $k$ , the calculation of $\Theta_{f_X,k} = \mathbb{E}[L_k(X)e^{-\frac{X}{2}}]$ is then computed through Taylor expansion of $x\mapsto e^x$ truncated at 40 terms, i.e.

$\Theta_{f_X,k} = \mathbb{E}[L_k(X)e^{-\frac{X}{2}}] \approx \mathbb{E}[\sum_{j=0}^k l_j X^j \sum_{n=0}^{40} \frac{(-X/2)^n}{n!} ] = \sum_{j=0}^k l_j \sum_{n=0}^{40} \frac{(-1)^n}{2^nn!}\mathbb{E}[X^{n+j}].$