README.md

In REndo: Fitting Linear Models with Endogenous Regressors using Latent Instrumental Variables

See our publication in JSS for more details on the methods and usage: doi:10.18637/jss.v107.i03

The REndo Package

Endogeneity arises when the independence assumption between an explanatory variable and the error in a statistical model is violated. Among its most common causes are omitted variable bias (e.g. like ability in the returns to education estimation), measurement error (e.g. survey response bias), or simultaneity (e.g. advertising and sales).

Instrumental variable estimation is a common treatment when endogeneity is of concern. However valid, strong external instruments are difficult to find. Consequently, statistical methods to correct for endogeneity without external instruments have been advanced. They are called internal instrumental variable models (IIV).

REndo implements the following instrument-free methods:

1) latent instrumental variables approach (Ebbes, Wedel, Boeckenholt, and Steerneman 2005)

2) higher moments estimation (Lewbel 1997)

3) heteroskedastic error approach (Lewbel 2012)

4) joint estimation using copula (Park and Gupta 2012)

5) multilevel GMM (Kim and Frees 2007)

The new version - REndo 2.0.0

The new version of REndo comes with a lot of improvements in terms of code optimization as well as different syntax for all functions.

Walk-Through

Below, we present the syntax for each of the 5 implemented instrument-free methods:

Latent Instrumental Variables

latentIV(y ~ P, data, start.params=c())

The first argument is the formula of the model to be estimated, y ~ P, where y is the response and P is the endogenous regressor. The second argument is the name of the dataset used and the last one, start.params=c(), which is optional, is a vector with the initial parameter values. When not indicated, the initial parameter values are taken to be the coefficients returned by the OLS estimator of y on P.

Copula Correction

copulaCorrection( y ~ X1 + X2 + P1 + P2 | continuous(P1) + discrete(P2), data, start.params=c(), num.boots)

The first argument is a two-part formula of the model to be estimated, with the second part of the RHS defining the endogenous regressor, here continuous(P1) + discrete(P2). The second argument is the name of the data, the third argument of the function, start.params, is optional and represents the initial parameter values supplied by the user (when missing, the OLS estimates are considered); while the fourth argument, num.boots, also optional, is the number of bootstraps to be performed (the default is 1000). Of course, defining the endogenous regressors depends on the number of endogenous regressors and their assumed distribution. Transformations of the explanatory variables, such as I(X), ln(X) are supported.

Higher Moments

higherMomentsIV(y ~ X1 + X2 + P | P | IIV(iiv = gp, g= x2, X1, X2) + IIV(iiv = yp) | Z1, data)

Here, y is the response; the first RHS of the formula, X1 + X2 + P, is the model to be estimated; the second part, P, specifies the endogenous regressors; the third part, IIV(), specifies the format of the internal instruments; the fourth part, Z1, is optional, allowing the user to add any external instruments available.

Regarding the third part of the formula, IIV(), it has a set of three arguments:

• iiv - specifies the form of the instrument,
• g - specifies the transformation to be done on the exogenous regressors,
• the set of exogenous variables from which the internal instruments should be built (it can be one or all of the exogenous variables).

A set of six instruments can be constructed, which should be specified in the iiv argument of IIV():

• g - for ,
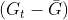• gp - for ,
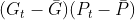• gy - for ,
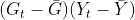• yp - for ,
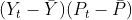• p2 - for ,
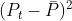• y2 - for .

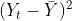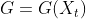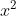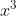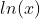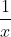where can be either , , or and should be specified in the g argument of the third RHS of the formula, as x2, x3, lnx or 1/x. In case of internal instruments built only from the endogenous regressor, e.g. p2, or from the response and the endogenous regressor, like for example in yp, there is no need to specify g or the set of exogenous regressors in the IIV() part of the formula. The function returns a set of tests for checking the validity of the instruments and the endogeneity assumption.

Heteroskedastic Errors

 hetErrorsIV(y ~ X1 + X2 + X3 + P | P | IIV(X1,X2) | Z1, data)

Here, y is the response variable, X1 + X2 + X3 + P represents the model to be estimated; the second part, P, specifies the endogenous regressors, the third part, IIV(X1, X2), specifies the exogenous heteroskedastic variables from which the instruments are derived, while the final part Z1 is optional, allowing the user to include additional external instrumental variables. Like in the higher moments approach, allowing the inclusion of additional external variables is a convenient feature of the function, since it increases the efficiency of the estimates. Transformation of the explanatory variables, such as I(X), ln(X) are possible both in the model specification as well as in the IIV() specification.

Multilevel GMM

multilevelIV(y ~ X11 + X12 + X21 + X22 + X23 + X31 + X33 + X34 + (1|CID) + (1|SID) | endo(X12), data)

The call of the function has a two-part formula and an argument for data specification. In the formula, the first part is the model specification, with fixed and random parameter specification, and the second part which specifies the regressors assumed endogenous, here endo(X12). The function returns the parameter estimates obtained with fixed effects, random effects and the GMM estimator proposed by Kim and Frees (2007), such that a comparison across models can be done.

Installation Instructions

Install the stable version from CRAN:

install.packages("REndo")

Install the development version from GitHub:

devtools::install_github("mmeierer/REndo", ref = "development")

REndo documentation built on July 3, 2024, 1:06 a.m.