README.md
In admmDensestSubmatrix: Alternating Direction Method of Multipliers to Solve Dense Dubmatrix Problem
admmDensenstSubmatrix 
Introduction
This is the R-package accompanying the paper Convex optimization for the densest subgraph and densest submatrix problems.
See also Matlab-code
The problem of identifying a dense submatrix is a fundamental problem in the analysis of matrix structure and complex networks. This package provides tools for identifying the densest submatrix of the fixed size in a given graph/matrix using first-order optimization methods.
See the tutorials below to get started.
Installation
#Install the development version from GitHub:
# install.packages("remotes")
remotes::install_github("pbombina/admmDensenstSubmatrix")
To also build the vignettes use:
#install.packages("remotes")
remotes::install_github("pbombina/admmDensenstSubmatrix", dependencies = TRUE,
build_vignettes = TRUE)
Usage
This section gives a brief overview of the different functions included in this package. For more details use help('function') or doc('function').
R-package contains the functions:
- plantedsubmatrix.R generates binary matrix sampled from dense submatrix of particular size
- densub.R ADMM algorithm for our relaxation of the densest subgraph and submatrix problems
- mat_shrink.R soft-threholding operator applied to vector of singular values (used in X-update step of densub.R)
Examples
We test this package on two different types of data: first, using random matrices sampled from the planted dense m x n submtarix model and, second, real-world collaboration and communication networks.
Random matrices
We first generate a random matrix with noise obscuring the planted submatrix using the function plantedsubmatrix. and then call the function densub to recover the planted submatrix.
# Initialize problem size and densities
# You can play around with these parameters
M <- 100 #number of rows of sampled matrix
N <- 200 #number of columns of sampled matrix
m <- 50 #number of rows of dense submatrix
n <- 40 #number of columns of dense submatrix
p <- 0.25 # noise density
q <- 0.85 #in-group density
#Make binary matrix with mn-submatrix
random<-plantedsubmatrix(M = M, N = N,m = m,n = n,p = p,q = q)
After generating the structure random containing the random matrix with desired planted structure, we can visually represent the matrix and planted submatrix as two-tone images, where dark pixels correspond to nonzero entries, and light pixels correspond to zero entries, using the following commands.
# Plot sampled G and matrix representations.
image(random$sampled_matrix, useRaster = TRUE, axes = FALSE, main = "Matrix A")
image(random$dense_submatrix, useRaster = TRUE, axes = FALSE, main = "Matrix X0")
image(random$disagreements, useRaster = TRUE, axes = FALSE, main = "Matrix Y0")
Tne vizualization of the randomly generated matrix 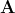 helps us to understand its structure. It is clear that
helps us to understand its structure. It is clear that 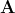 contains a dense
contains a dense 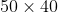 block (in the bottom left corner).
block (in the bottom left corner).
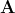](https://github.com/pbombina/admmDensenstSubmatrix/blob/master/vignettes/Rplot.jpeg?raw=true)
We can remove all noise and isolate an image of a rank-one matrix 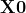 with
with 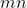 nonzero entries.
nonzero entries.
Then we vizualize matrix 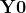 to see the number of disagreements between original matrix
to see the number of disagreements between original matrix 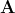 and
and 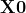 .
.

We call the ADMM solver and visualize the output using the following commands.
#Call ADMM solver
admm <- densub(G = random$sampled_matrix, m = m, n = n, tau = 0.35, gamma = 6/(sqrt(m*n)*(q-p)), opt_tol = 1.0e-4,maxiter = 500, quiet = TRUE)
#Plot results
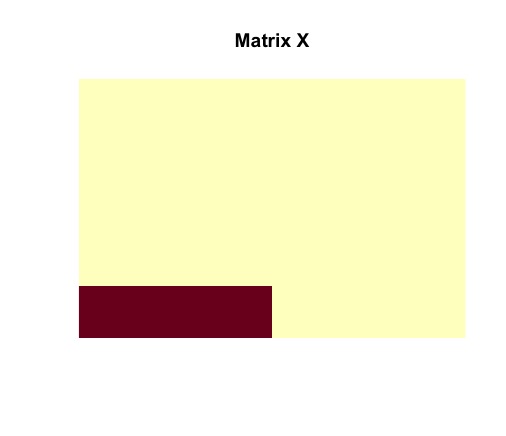
image(admm$X, useRaster = TRUE, axes = FALSE, main = "Matrix X")
image(admm$Y, useRaster = TRUE, axes = FALSE, main = "Matrix Y")
The ADMM solver returns the optimal solutions 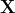 and
and 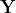 . It must be noted that matrices
. It must be noted that matrices 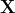 and
and 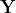 are identical to the actual structures of
are identical to the actual structures of 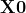 and
and 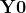 . The planted submatrix is recovered.
. The planted submatrix is recovered.

Collaboration Network
The following is a simple example on how one could use the package to analyze the collaboration network found in the JAZZ dataset. It is known that this network contains a cluster of 100 musicians which performed together.

We have already prepared dataset to work with. More details can be found in the provided file JAZZ_IN_R.R ( in vignettes folder).
#Load dataset
load(file = "JAZZ.RData")
#Initialize problem size and densities
G <- new #define matrix G equivalent to JAZZ dataset
m <- 100 #clique size or the number of rows of the dense submatrix
n <- 100 #clique size of the number of columns of the dense sumbatrix
tau <- 0.85 #regularization parameter
opt_tol <- 1.0e-2 #optimal tolerance
maxiter <- 2000 #number of iterations
gamma <- 8/n #regularization parameter
#call ADMM solver
admm <- densub(G = G, m = m, n = n, tau = tau, gamma = gamma, opt_tol = opt_tol, maxiter=maxiter, quiet = TRUE)
# Planted solution X0
X0 <- matrix(0L, nrow = 198, ncol = 198) #construct rank-one matrix X0
X0[1:100,1:100] <- matrix(1L, nrow = 100, ncol = 100)#define dense block
# Planted solution Y0
Y0 <- matrix(0L, nrow = 198, ncol = 198) #construct matrix for counting disagreements between G and X0
Y0[1:100,1:100] < matrix(1L,nrow = 100,ncol = 1000)-G[1:100,1:100]
#Check primal and dual residuals
C <- admm$X-X0
a <- norm(C, "F") #Frobenius norm of matrix C
b <- norm(X0,"F") #Frobenius norm of matrix X0
recovery <- matrix(0L,nrow = 1, ncol = 1)#create recovery condition matrix
if (a/b^2<opt_tol){ #Recovery condition
recovery = recovery+1
} else {
recovery = 0
}
Our algorithm converges to the dense submatrix representing the community of 100 musicians after 50 iterations.
How to contribute
- Fork, clone, edit, commit, push, create pull request
- Use RStudio
Reporting bugs and other issues
If you encounter a clear bug, please file a minimal reproducible example on github.
Try the admmDensestSubmatrix package in your browser
Any scripts or data that you put into this service are public.
admmDensestSubmatrix documentation built on Oct. 31, 2019, 5:33 p.m.
admmDensenstSubmatrix 
Introduction
This is the R-package accompanying the paper Convex optimization for the densest subgraph and densest submatrix problems.
See also Matlab-code
The problem of identifying a dense submatrix is a fundamental problem in the analysis of matrix structure and complex networks. This package provides tools for identifying the densest submatrix of the fixed size in a given graph/matrix using first-order optimization methods.
See the tutorials below to get started.
Installation
#Install the development version from GitHub:
# install.packages("remotes")
remotes::install_github("pbombina/admmDensenstSubmatrix")
To also build the vignettes use:
#install.packages("remotes")
remotes::install_github("pbombina/admmDensenstSubmatrix", dependencies = TRUE,
build_vignettes = TRUE)
Usage
This section gives a brief overview of the different functions included in this package. For more details use help('function') or doc('function').
R-package contains the functions:
- plantedsubmatrix.R generates binary matrix sampled from dense submatrix of particular size
- densub.R ADMM algorithm for our relaxation of the densest subgraph and submatrix problems
- mat_shrink.R soft-threholding operator applied to vector of singular values (used in X-update step of densub.R)
Examples
We test this package on two different types of data: first, using random matrices sampled from the planted dense m x n submtarix model and, second, real-world collaboration and communication networks.
Random matrices
We first generate a random matrix with noise obscuring the planted submatrix using the function plantedsubmatrix. and then call the function densub to recover the planted submatrix.
# Initialize problem size and densities
# You can play around with these parameters
M <- 100 #number of rows of sampled matrix
N <- 200 #number of columns of sampled matrix
m <- 50 #number of rows of dense submatrix
n <- 40 #number of columns of dense submatrix
p <- 0.25 # noise density
q <- 0.85 #in-group density
#Make binary matrix with mn-submatrix
random<-plantedsubmatrix(M = M, N = N,m = m,n = n,p = p,q = q)
After generating the structure random containing the random matrix with desired planted structure, we can visually represent the matrix and planted submatrix as two-tone images, where dark pixels correspond to nonzero entries, and light pixels correspond to zero entries, using the following commands.
# Plot sampled G and matrix representations.
image(random$sampled_matrix, useRaster = TRUE, axes = FALSE, main = "Matrix A")
image(random$dense_submatrix, useRaster = TRUE, axes = FALSE, main = "Matrix X0")
image(random$disagreements, useRaster = TRUE, axes = FALSE, main = "Matrix Y0")
Tne vizualization of the randomly generated matrix helps us to understand its structure. It is clear that
contains a dense
block (in the bottom left corner).
](https://github.com/pbombina/admmDensenstSubmatrix/blob/master/vignettes/Rplot.jpeg?raw=true)
We can remove all noise and isolate an image of a rank-one matrix with
nonzero entries.

Then we vizualize matrix to see the number of disagreements between original matrix
and
.

We call the ADMM solver and visualize the output using the following commands.
#Call ADMM solver
admm <- densub(G = random$sampled_matrix, m = m, n = n, tau = 0.35, gamma = 6/(sqrt(m*n)*(q-p)), opt_tol = 1.0e-4,maxiter = 500, quiet = TRUE)
#Plot results
image(admm$X, useRaster = TRUE, axes = FALSE, main = "Matrix X")
image(admm$Y, useRaster = TRUE, axes = FALSE, main = "Matrix Y")
The ADMM solver returns the optimal solutions and
. It must be noted that matrices
and
are identical to the actual structures of
and
. The planted submatrix is recovered.


Collaboration Network
The following is a simple example on how one could use the package to analyze the collaboration network found in the JAZZ dataset. It is known that this network contains a cluster of 100 musicians which performed together.

We have already prepared dataset to work with. More details can be found in the provided file JAZZ_IN_R.R ( in vignettes folder).
#Load dataset
load(file = "JAZZ.RData")
#Initialize problem size and densities
G <- new #define matrix G equivalent to JAZZ dataset
m <- 100 #clique size or the number of rows of the dense submatrix
n <- 100 #clique size of the number of columns of the dense sumbatrix
tau <- 0.85 #regularization parameter
opt_tol <- 1.0e-2 #optimal tolerance
maxiter <- 2000 #number of iterations
gamma <- 8/n #regularization parameter
#call ADMM solver
admm <- densub(G = G, m = m, n = n, tau = tau, gamma = gamma, opt_tol = opt_tol, maxiter=maxiter, quiet = TRUE)
# Planted solution X0
X0 <- matrix(0L, nrow = 198, ncol = 198) #construct rank-one matrix X0
X0[1:100,1:100] <- matrix(1L, nrow = 100, ncol = 100)#define dense block
# Planted solution Y0
Y0 <- matrix(0L, nrow = 198, ncol = 198) #construct matrix for counting disagreements between G and X0
Y0[1:100,1:100] < matrix(1L,nrow = 100,ncol = 1000)-G[1:100,1:100]
#Check primal and dual residuals
C <- admm$X-X0
a <- norm(C, "F") #Frobenius norm of matrix C
b <- norm(X0,"F") #Frobenius norm of matrix X0
recovery <- matrix(0L,nrow = 1, ncol = 1)#create recovery condition matrix
if (a/b^2<opt_tol){ #Recovery condition
recovery = recovery+1
} else {
recovery = 0
}
Our algorithm converges to the dense submatrix representing the community of 100 musicians after 50 iterations.
How to contribute
- Fork, clone, edit, commit, push, create pull request
- Use RStudio
Reporting bugs and other issues
If you encounter a clear bug, please file a minimal reproducible example on github.
Try the admmDensestSubmatrix package in your browser
Any scripts or data that you put into this service are public.
Add the following code to your website.
For more information on customizing the embed code, read Embedding Snippets.
