README.md
In freealg: The Free Algebra
The Free Algebra in R

Overview
The free algebra is an interesting and useful object. Here I present the
freealg package which provides some functionality for free algebra in
the R programming environment. The package uses the C++ map class for
efficiency and conforms to disordR discipline. Several use-cases are
provided.
Installation
You can install the released version of freealg from
CRAN with:
# install.packages("freealg") # uncomment this to install the package
library("freealg")
The free algebra
The free algebra is the free R-module with a basis consisting of all
words over an alphabet of symbols with multiplication of words defined
as concatenation. Thus, with an alphabet of
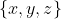 and
and
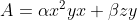
and
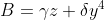
we would have

and
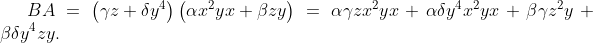
A natural and easily implemented extension is to use upper-case symbols
to represent multiplicative inverses of the lower-case equivalents
(formally we would use the presentation
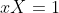 ). Thus if
). Thus if
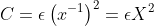
we would have
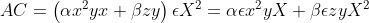
and
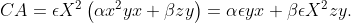
The system inherits associativity from associativity of concatenation,
and distributivity is assumed, but it is not commutative.
The freealg package in use
Creating a free algebra object is straightforward. We can coerce from a
character string with natural idiom:
X <- as.freealg("1 + 3a + 5b + 5abba")
X
#> free algebra element algebraically equal to
#> + 1 + 3*a + 5*abba + 5*b
or use a more formal method:
freealg(sapply(1:5,seq_len),1:5)
#> free algebra element algebraically equal to
#> + a + 2*ab + 3*abc + 4*abcd + 5*abcde
Y <- as.freealg("6 - 4a +2aaab")
X+Y
#> free algebra element algebraically equal to
#> + 7 - a + 2*aaab + 5*abba + 5*b
X*Y
#> free algebra element algebraically equal to
#> + 6 + 14*a - 12*aa + 6*aaaab + 2*aaab + 30*abba - 20*abbaa + 10*abbaaaab + 30*b
#> - 20*ba + 10*baaab
X^2
#> free algebra element algebraically equal to
#> + 1 + 6*a + 9*aa + 15*aabba + 15*ab + 10*abba + 15*abbaa + 25*abbaabba +
#> 25*abbab + 10*b + 15*ba + 25*babba + 25*bb
We can demonstrate associativity (which is non-trivial):
set.seed(0)
(x1 <- rfalg(inc=TRUE))
#> free algebra element algebraically equal to
#> + 7*C + 6*Ca + 4*B + 3*BC + a + 5*aCBB + 2*bc
(x2 <- rfalg(inc=TRUE))
#> free algebra element algebraically equal to
#> + 6 + CAAA + 2*Ca + 3*Cbcb + 7*aaCA + 4*b + 5*c
(x3 <- rfalg(inc=TRUE))
#> free algebra element algebraically equal to
#> + 3*C + 5*CbAc + BACB + 2*a + 10*b + 7*cb
(function rfalg() generates random freealg objects). Then
x1*(x2*x3) == (x1*x2)*x3
#> [1] TRUE
Further information
For more detail, see the package vignette
vignette("freealg")
Try the freealg package in your browser
Any scripts or data that you put into this service are public.
freealg documentation built on Sept. 12, 2024, 7:08 a.m.
The Free Algebra in R

Overview
The free algebra is an interesting and useful object. Here I present the
freealg package which provides some functionality for free algebra in
the R programming environment. The package uses the C++ map class for
efficiency and conforms to disordR discipline. Several use-cases are
provided.
Installation
You can install the released version of freealg from
CRAN with:
# install.packages("freealg") # uncomment this to install the package
library("freealg")
The free algebra
The free algebra is the free R-module with a basis consisting of all
words over an alphabet of symbols with multiplication of words defined
as concatenation. Thus, with an alphabet of
and
and
we would have
and
A natural and easily implemented extension is to use upper-case symbols
to represent multiplicative inverses of the lower-case equivalents
(formally we would use the presentation
). Thus if
we would have
and
The system inherits associativity from associativity of concatenation, and distributivity is assumed, but it is not commutative.
The freealg package in use
Creating a free algebra object is straightforward. We can coerce from a character string with natural idiom:
X <- as.freealg("1 + 3a + 5b + 5abba")
X
#> free algebra element algebraically equal to
#> + 1 + 3*a + 5*abba + 5*b
or use a more formal method:
freealg(sapply(1:5,seq_len),1:5)
#> free algebra element algebraically equal to
#> + a + 2*ab + 3*abc + 4*abcd + 5*abcde
Y <- as.freealg("6 - 4a +2aaab")
X+Y
#> free algebra element algebraically equal to
#> + 7 - a + 2*aaab + 5*abba + 5*b
X*Y
#> free algebra element algebraically equal to
#> + 6 + 14*a - 12*aa + 6*aaaab + 2*aaab + 30*abba - 20*abbaa + 10*abbaaaab + 30*b
#> - 20*ba + 10*baaab
X^2
#> free algebra element algebraically equal to
#> + 1 + 6*a + 9*aa + 15*aabba + 15*ab + 10*abba + 15*abbaa + 25*abbaabba +
#> 25*abbab + 10*b + 15*ba + 25*babba + 25*bb
We can demonstrate associativity (which is non-trivial):
set.seed(0)
(x1 <- rfalg(inc=TRUE))
#> free algebra element algebraically equal to
#> + 7*C + 6*Ca + 4*B + 3*BC + a + 5*aCBB + 2*bc
(x2 <- rfalg(inc=TRUE))
#> free algebra element algebraically equal to
#> + 6 + CAAA + 2*Ca + 3*Cbcb + 7*aaCA + 4*b + 5*c
(x3 <- rfalg(inc=TRUE))
#> free algebra element algebraically equal to
#> + 3*C + 5*CbAc + BACB + 2*a + 10*b + 7*cb
(function rfalg() generates random freealg objects). Then
x1*(x2*x3) == (x1*x2)*x3
#> [1] TRUE
Further information
For more detail, see the package vignette
vignette("freealg")
Try the freealg package in your browser
Any scripts or data that you put into this service are public.
Add the following code to your website.
For more information on customizing the embed code, read Embedding Snippets.
