README.md

In ChrisBogner/ViscousFlow: Analysis of tracer experiments with the viscous flow approach by Peter Germann

ViscousFlow

Christina Bogner 2021-06-11

Package aims

This package analyses laboratory irrigation experiments on soil columns. It uses the viscous flow approach by Germann (2018).

Installation

You can install ViscousFlow from GitHub with `devoolts’ like so:

# install.packages("devtools")
devtools::install_github("ChrisBogner/ViscousFlow")

Example

This is a basic example which shows you how to fit the viscous flow equation to the decreasing limb of a drainage curve and to calculate the viscous flow parameters 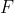and .

The package contains two data sets, namely tracer and drainage. Both originate from the publication by Bogner and Germann (2019). There, it is called column C1 and was packed from loose soil material (diameter = 15 cm and height = 30 cm) collected form a forest soil in southeast Germany (50°08’32.8’’ N 11°51’52.9’’ E). Prior to the irrigation experiment, the soil column was saturated from below and then drained to field capacity. It was irrigated at 10 mm h-1 during 64410 sec (17.9 h). During the experiment, a suction of -10 hPa was applied at the bottom of the soil column to prevent saturation. The data set drainage contains the drainage from this soil column C1.

The irrigation water contained Bromide that was measured in the drainage water with an ion-sensitive electrode. The data set tracer contains the normalized Bromide concentration (i.e. concentration in the drainage divided by the concentration in the irrigation water).

Both data sets were smoothed by LOESS (see the original open access publication Bogner and Germann (2019) for details).

Load libraries and data.

library(ViscousFlow)
library(tidyverse)
#> ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.1 ──
#> ✓ ggplot2 3.3.3     ✓ purrr   0.3.4
#> ✓ tibble  3.1.2     ✓ dplyr   1.0.6
#> ✓ tidyr   1.1.3     ✓ stringr 1.4.0
#> ✓ readr   1.4.0     ✓ forcats 0.5.1
#> ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
#> x dplyr::filter() masks stats::filter()
#> x dplyr::lag()    masks stats::lag()
library(gridExtra)
#> 
#> Attache Paket: 'gridExtra'
#> Das folgende Objekt ist maskiert 'package:dplyr':
#> 
#>     combine

data(drainage)
data(tracer)

Define TB and TE, the start and end times of the irrigation experiment.

TB <- 0
TE <- 64410

Plot the data.

g_all <- list(geom_line(),
  xlab('Time since start of irrigataion(sec)'),
  geom_vline(aes(xintercept = TE, col = 'TE'), lty = 2),
  scale_colour_manual(name = ' ', values = ('end of irrigation' = 'blue'),
                      labels = 'end of irrigation'),
  theme(legend.position=c(0.2, 0.9), 
        legend.background = element_rect(fill="transparent", colour=NA),          legend.key = element_rect(fill = "white"))
)

g1 <- ggplot(data = drainage, aes(x = time_sec, y = q_mmh)) + 
  g_all +
  ylab(expression(paste('Drainage  (mm ', h^{-1}, ')'))) +
  ggtitle('Drainage column C1')

g2 <- ggplot(data = tracer, aes(x = time, y = value)) + 
  g_all +
    ylab(expression(c/c[0]))  +
  ggtitle('Tracer breakthrough column C1')

grid.arrange(g1, g2, ncol = 1)

Calculate the breakthrough time of the tracer. The breakthrough time is defined as the largest curvature in time_interval.

breakthrough <- find_tracer_breakthrough(tracer_data = tracer, time_interval = c(30000, 40000), do_plot = T)

breakthrough
#> $breakthrough_time
#> [1] 37169
#> 
#> $tracer_data
#> # A tibble: 213 x 6
#>     time     value smoothed_tracer tracer_first_der… curvature curvature_first_…
#>    <dbl>     <dbl>           <dbl>             <dbl>     <dbl>             <dbl>
#>  1  1560  0.00205        0.00201        -0.000000920  5.13e-11          3.74e-14
#>  2  1920  0.00171        0.00168        -0.000000902  6.51e-11          3.46e-14
#>  3  2280  0.00138        0.00136        -0.000000875  7.58e-11          2.11e-14
#>  4  2640  0.00106        0.00105        -0.000000845  8.17e-11          6.11e-15
#>  5  3000  0.000745       0.000753       -0.000000816  8.08e-11         -1.11e-15
#>  6  3360  0.000449       0.000464       -0.000000789  7.83e-11         -2.57e-15
#>  7  3720  0.000167       0.000186       -0.000000760  7.93e-11         -3.24e-16
#>  8  4080 -0.000101      -0.0000825      -0.000000730  8.07e-11          9.50e-16
#>  9  4440 -0.000359      -0.000340       -0.000000702  7.97e-11         -3.44e-15
#> 10  4800 -0.000608      -0.000588       -0.000000674  7.72e-11         -7.70e-15
#> # … with 203 more rows

Fit the viscous flow equation to the drainage data:

During the steady state, the irrigation intensity and the drainage flow should be equal. From experience, calculating the flux density 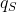from the plateau of the drainage flow leads to a better fit. Therefore, we set the parameter fit_qS = TRUE.

fit_result <- fit_drainage_tail(drainage_data = drainage, stationary_time = c(0.9 * 64410 , 64410), TE = 64410, D = 0.15,
                              qS = NULL, fit_qS = TRUE, delta_t = 30,
                              my_weights = 1)
#> Warning in stats::optimize(fit_TD, interval = TD_interval, weights =
#> my_weights, : NA/Inf durch größte positive Zahl ersetzt

#> Warning in stats::optimize(fit_TD, interval = TD_interval, weights =
#> my_weights, : NA/Inf durch größte positive Zahl ersetzt

The arrival times of the wetting () and drainage () fronts equal:

fit_result$TW
#> [1] 1260
fit_result$TD
#> [1] 64830

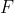Calculate the parameters of the viscous flow, namely the celerity , the film width (in 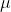m) and the contact area (in m-1).

params <- calculate_vf_parameters(TD = fit_result$TD, TE = fit_result$TE,
                                  Z = 0.3, qS = fit_result$qS)
params
#>              c        F        L
#> 1 0.0007142857 8.532995 1376.101

Refereneces

Bogner, Christina, and Peter Germann. 2019. “Viscous Flow Approach to ‘Pushing Out Old Water’ from Undisturbed and Repacked Soil Columns.” *Vadose Zone Journal* 18 (1): 180168. .

Germann, Peter. 2018. *Preferential Flow Stokes Approach to Infiltration and Drainage*. CH: Geographica Bernensia. https://doi.org/.

ChrisBogner/ViscousFlow documentation built on June 13, 2021, 7:47 a.m.