README.md
In Goodgolden/LDTM: Longitudinal Dirichlet Tree Multinomial Model
TEST
LDTM
The goal of LDTM is to …
Installation
You can install the development version of LDTM from
GitHub with:
# install.packages("devtools")
devtools::install_github("Goodgolden/LDTM")
Example
This is a basic example which shows you how to solve a common problem:
library(LDTM)
#> Loading required package: tidyverse
#> ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.1 ──
#> ✔ ggplot2 3.3.5 ✔ purrr 0.3.4
#> ✔ tibble 3.1.6 ✔ dplyr 1.0.8
#> ✔ tidyr 1.2.0 ✔ stringr 1.4.0
#> ✔ readr 2.1.2 ✔ forcats 0.5.1
#> ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
#> ✖ dplyr::filter() masks stats::filter()
#> ✖ dplyr::lag() masks stats::lag()
#> Welcome to my package
## basic example code
Introduction
OTU operational taxonomic units
microbial genomic sequencess clustered by sequence similarity
partition sequences into discrete groups instead of traditional
taxonomic units.
the most abundant sequence in an OTU is the representative sequence
representative sequences from all the OTUs are used to construct a
phylogenetic tree among all the OTUs
Microbial community information == OTUs + counts + phylogenetic
relationship + taxonomy
Human gut microbiome study in University of Pennsylvania
the effect of diet on gut microbiome composition
- gut microbiome data
- nutrient intake data
distance based analysis
-
identify a few gut microbiome associated nutrients
-
unable to provide information on how dietary nutrient affect
bacterial taxa
Goal
identify both the key nutrients as well as the taxa the nutrient affect
Chen and Li (2013) adopted a regression-based approach
OTU abundance data as multivariate count responses, and nutrient as
covaraite
Model
Multinomial logistic regression





The link function is a multinomial-Poisson transformation
might need to use Poissonization to simulate the data
Overdisperson
-
the multinomial distribution is not appropriate
-
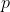 is a random variable with some prior distribution
is a random variable with some prior distribution
-
 is a (d-1) dimensional simplex,
is a (d-1) dimensional simplex,
-
the support of p is

-
Dirichlet distribution density at

-
Dirichlet is a conjugate prior to multinomial distribution
-
posterior is Dirichlet multionmial distribution, aka the Dirichlet
compound multinomial distribution.




Limitation
-
all components must share a common variance parameter
-
components are mutually independent, up to the constraint that must
sum up to 1
-
distribution fails to take into account the special and inherent
property of microbiome count data (evolutionary relationships in the
phylogenetic tree)
Generalization of Dirichlet Multinomial distribution
-
the relationships among the components of the count vector can be
represented as a tree, node-by-node.
-
each component has a independent variance
-
components are correlated at subtree levels
-
a regression model with the effects of covariates
-
a regularized methods for selecting covarites (nutrients) that are
associated with the count responses (OTUs)
Logistic Normal Multinomial distribution
-
Billheimer with Aitchison’s logistic normal distribution instead of
Dirichlet
- covaraites to the count vector (Billheimer et al. 2001)
- link dietary nutrients with bacteria counts (Xia et al. 2013)
- cannot exploit the tree structure information, logistic normal
multinomial does not have a closed-form expression.
Dirichlet-Tree Multinomial Distributions
-
total number of counts, determined by the sequence depth, as an
ancillary statistics
- analysis conditioning on this number
-
A Tree
 representing the hierarchical structure over the count responses
representing the hierarchical structure over the count responses
-
we will incorporate the tree structural information into the
modeling
-
 the set of leaf nodes
the set of leaf nodes
-
 the set of internal nodes of
the set of internal nodes of

-
for each
 ,
,
 the child nodes of
the child nodes of

-
for each
 and
and
 ,
,

-

-

-

-
 is the index for the subtree counts and probabilities
is the index for the subtree counts and probabilities
-
Let
 to be the root node of
to be the root node of
 .
.
-
each leaf node is

- the path from
 to
to
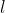 ,
where
,
where

 is the inner branches in this path
is the inner branches in this path ,
with the
,
with the
 that each branch as a probability (a conditional probability
given we know where the branch started).
that each branch as a probability (a conditional probability
given we know where the branch started).

-
for
 is the product of branch probabilities from root
is the product of branch probabilities from root
 to final leaf
to final leaf
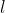
-
this is for the leaf level


- this is for the internal nodes
 the joint density of
the joint density of
 has the form of:
has the form of:

-

-
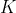 is the number of children of
is the number of children of

-




-
that each component in the product
 corresponds to a interior node in the tree
corresponds to a interior node in the tree
-
the Dirichlet multinomial distribution based on the accumulated
counts along branches of given node.
![E[p_l] = \prod_{v\in\mathcal V} \prod_{c\in\mathcal C_v}\bigg(E[b_{vc}] \bigg)^{\delta_{vc}(l)} = \prod_{v\in\mathcal V} \prod_{c\in\mathcal C_v}\bigg( \frac {\alpha_{vc}} {\sum_{c\in \mathcal C_v} \alpha_{vc}} \bigg)^{\delta_{vc}(l)}](https://latex.codecogs.com/png.image?%5Cdpi%7B110%7D&space;%5Cbg_white&space;E%5Bp_l%5D%20%3D%20%5Cprod_%7Bv%5Cin%5Cmathcal%20V%7D%20%5Cprod_%7Bc%5Cin%5Cmathcal%20C_v%7D%5Cbigg%28E%5Bb_%7Bvc%7D%5D%20%5Cbigg%29%5E%7B%5Cdelta_%7Bvc%7D%28l%29%7D%20%3D%20%5Cprod_%7Bv%5Cin%5Cmathcal%20V%7D%20%5Cprod_%7Bc%5Cin%5Cmathcal%20C_v%7D%5Cbigg%28%20%5Cfrac%20%7B%5Calpha_%7Bvc%7D%7D%20%7B%5Csum_%7Bc%5Cin%20%5Cmathcal%20C_v%7D%20%5Calpha_%7Bvc%7D%7D%20%5Cbigg%29%5E%7B%5Cdelta_%7Bvc%7D%28l%29%7D)
-
given
![\sum_{k=1}^K Y_k = \sum_{k=1}^K y_k; \ E[Y_l] = E[p_l] \sum_{k=1} ^Ky_k](https://latex.codecogs.com/png.image?%5Cdpi%7B110%7D&space;%5Cbg_white&space;%5Csum_%7Bk%3D1%7D%5EK%20Y_k%20%3D%20%5Csum_%7Bk%3D1%7D%5EK%20y_k%3B%20%5C%20E%5BY_l%5D%20%3D%20E%5Bp_l%5D%20%5Csum_%7Bk%3D1%7D%20%5EKy_k)
- when
 ,
each
,
each
 has an independent variance
has an independent variance
- two components
 with in the same subtree indexed by
with in the same subtree indexed by
 are correlated, due to the same ancestor of
are correlated, due to the same ancestor of
 .
.
Dirichlet Tree Multinomial Regression Model
-
a regression of
 on
on
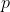 covariates
covariates

-
for each
 and
and
 we express
we express
 as a linear combination of the covariates.
as a linear combination of the covariates.













![l_v(\beta_v) = log L_v(\beta_v) = \sum_{i=1}^n \Bigg[\tilde \Gamma \Big(\sum_{c\in \mathcal C_v} \alpha_{ivc}\Big) - \tilde \Gamma \Big(\sum_{c\in \mathcal C_v} y_{ivc} + \sum_{c\in \mathcal C_v} \alpha_{ivc}\Big) +c\sum_{c \in \mathcal C_v} \bigg\{ \tilde \Gamma \Big(y_{ivc} + \alpha_{ivc}\Big) - \tilde \Gamma \Big(\alpha_{ivc}\Big) \bigg\}\Bigg]](https://latex.codecogs.com/png.image?%5Cdpi%7B110%7D&space;%5Cbg_white&space;l_v%28%5Cbeta_v%29%20%3D%20log%20L_v%28%5Cbeta_v%29%20%3D%20%5Csum_%7Bi%3D1%7D%5En%20%5CBigg%5B%5Ctilde%20%5CGamma%20%5CBig%28%5Csum_%7Bc%5Cin%20%5Cmathcal%20C_v%7D%20%5Calpha_%7Bivc%7D%5CBig%29%20-%20%5Ctilde%20%5CGamma%20%5CBig%28%5Csum_%7Bc%5Cin%20%5Cmathcal%20C_v%7D%20y_%7Bivc%7D%20%2B%20%5Csum_%7Bc%5Cin%20%5Cmathcal%20C_v%7D%20%5Calpha_%7Bivc%7D%5CBig%29%20%2Bc%5Csum_%7Bc%20%5Cin%20%5Cmathcal%20C_v%7D%20%5Cbigg%5C%7B%20%5Ctilde%20%5CGamma%20%5CBig%28y_%7Bivc%7D%20%2B%20%5Calpha_%7Bivc%7D%5CBig%29%20-%20%5Ctilde%20%5CGamma%20%5CBig%28%5Calpha_%7Bivc%7D%5CBig%29%20%5Cbigg%5C%7D%5CBigg%5D)



![l_v(\beta_v) = \log L_v(\beta_v) = \sum_{i=1}^n \Bigg[\log \bigg(\Gamma \Big(\sum_{c\in \mathcal C_v} \exp(x_i^T\beta_{vc})\Big) \bigg) - \log \bigg(\Gamma \Big(\sum_{c\in \mathcal C_v} y_{ivc} + \sum_{c\in \mathcal C_v} \exp(x_i^T\beta_{vc})\Big) \bigg) +\sum_{c \in \mathcal C_v} \bigg\{ \log \bigg(\Gamma \Big(y_{ivc} + \exp(x_i^T\beta_{vc})\Big)\bigg) -\log \bigg(\Gamma \Big(\exp(x_i^T\beta_{vc})\Big) \bigg)\bigg\}\Bigg]](https://latex.codecogs.com/png.image?%5Cdpi%7B110%7D&space;%5Cbg_white&space;l_v%28%5Cbeta_v%29%20%3D%20%5Clog%20L_v%28%5Cbeta_v%29%20%3D%20%5Csum_%7Bi%3D1%7D%5En%20%5CBigg%5B%5Clog%20%5Cbigg%28%5CGamma%20%5CBig%28%5Csum_%7Bc%5Cin%20%5Cmathcal%20C_v%7D%20%5Cexp%28x_i%5ET%5Cbeta_%7Bvc%7D%29%5CBig%29%20%5Cbigg%29%20-%20%5Clog%20%5Cbigg%28%5CGamma%20%5CBig%28%5Csum_%7Bc%5Cin%20%5Cmathcal%20C_v%7D%20y_%7Bivc%7D%20%2B%20%5Csum_%7Bc%5Cin%20%5Cmathcal%20C_v%7D%20%5Cexp%28x_i%5ET%5Cbeta_%7Bvc%7D%29%5CBig%29%20%5Cbigg%29%20%2B%5Csum_%7Bc%20%5Cin%20%5Cmathcal%20C_v%7D%20%5Cbigg%5C%7B%20%5Clog%20%5Cbigg%28%5CGamma%20%5CBig%28y_%7Bivc%7D%20%2B%20%5Cexp%28x_i%5ET%5Cbeta_%7Bvc%7D%29%5CBig%29%5Cbigg%29%20-%5Clog%20%5Cbigg%28%5CGamma%20%5CBig%28%5Cexp%28x_i%5ET%5Cbeta_%7Bvc%7D%29%5CBig%29%20%5Cbigg%29%5Cbigg%5C%7D%5CBigg%5D)
Regularized Likelihood Estimation
-
parametrization for Dirichlet Tree Multinomial Regression Model
-
the number of
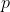 time the number of tree branches
time the number of tree branches


Algorithm of accelerated proximal gradient method
-
approximate
 at
at






![\beta_{vc}^{(t+1)} = \underset {\beta_{vc}} {argmin} \Bigg[ \frac 1 2 \bigg \\|\beta_{vc} - \Big\{\eta_{vc}^{(t)} - \frac 1 C \nabla l_{vc} (\eta_v^{(t)}) \Big\}\bigg\\|_2^2 + \frac {\lambda_1} {C}\\|\beta_{vc}\\|_1 + \frac {\lambda_2} {C} \\|\beta_{vc}\\|_2 \Bigg]](https://latex.codecogs.com/png.image?%5Cdpi%7B110%7D&space;%5Cbg_white&space;%5Cbeta_%7Bvc%7D%5E%7B%28t%2B1%29%7D%20%3D%20%5Cunderset%20%7B%5Cbeta_%7Bvc%7D%7D%20%7Bargmin%7D%20%5CBigg%5B%20%5Cfrac%201%202%20%5Cbigg%20%5C%7C%5Cbeta_%7Bvc%7D%20-%20%5CBig%5C%7B%5Ceta_%7Bvc%7D%5E%7B%28t%29%7D%20-%20%5Cfrac%201%20C%20%5Cnabla%20l_%7Bvc%7D%20%28%5Ceta_v%5E%7B%28t%29%7D%29%20%5CBig%5C%7D%5Cbigg%5C%7C_2%5E2%20%2B%20%5Cfrac%20%7B%5Clambda_1%7D%20%7BC%7D%5C%7C%5Cbeta_%7Bvc%7D%5C%7C_1%20%2B%20%5Cfrac%20%7B%5Clambda_2%7D%20%7BC%7D%20%5C%7C%5Cbeta_%7Bvc%7D%5C%7C_2%20%5CBigg%5D)
![\text {s.t.} \ \ \beta_{vc}^{(t+1)} = \underset {\beta_{vc}} {argmin} \Bigg[ \frac 1 2 \bigg \\| \beta_{vc} +\frac 1 C \nabla l_{vc} (0) \bigg\\|_2^2 + \lambda \bigg(\frac {1-\gamma} {C}\\|\beta_{vc}\\|_1 + \frac {\gamma} {C} \\|\beta_{vc}\\|_2\bigg) \Bigg]](https://latex.codecogs.com/png.image?%5Cdpi%7B110%7D&space;%5Cbg_white&space;%5Ctext%20%7Bs.t.%7D%20%5C%20%5C%20%5Cbeta_%7Bvc%7D%5E%7B%28t%2B1%29%7D%20%3D%20%5Cunderset%20%7B%5Cbeta_%7Bvc%7D%7D%20%7Bargmin%7D%20%5CBigg%5B%20%5Cfrac%201%202%20%5Cbigg%20%5C%7C%20%5Cbeta_%7Bvc%7D%20%2B%5Cfrac%201%20C%20%5Cnabla%20l_%7Bvc%7D%20%280%29%20%5Cbigg%5C%7C_2%5E2%20%2B%20%5Clambda%20%5Cbigg%28%5Cfrac%20%7B1-%5Cgamma%7D%20%7BC%7D%5C%7C%5Cbeta_%7Bvc%7D%5C%7C_1%20%2B%20%5Cfrac%20%7B%5Cgamma%7D%20%7BC%7D%20%5C%7C%5Cbeta_%7Bvc%7D%5C%7C_2%5Cbigg%29%20%5CBigg%5D)


Goodgolden/LDTM documentation built on May 25, 2022, 5:25 p.m.
TEST
LDTM
The goal of LDTM is to …
Installation
You can install the development version of LDTM from GitHub with:
# install.packages("devtools")
devtools::install_github("Goodgolden/LDTM")
Example
This is a basic example which shows you how to solve a common problem:
library(LDTM)
#> Loading required package: tidyverse
#> ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.1 ──
#> ✔ ggplot2 3.3.5 ✔ purrr 0.3.4
#> ✔ tibble 3.1.6 ✔ dplyr 1.0.8
#> ✔ tidyr 1.2.0 ✔ stringr 1.4.0
#> ✔ readr 2.1.2 ✔ forcats 0.5.1
#> ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
#> ✖ dplyr::filter() masks stats::filter()
#> ✖ dplyr::lag() masks stats::lag()
#> Welcome to my package
## basic example code
Introduction
OTU operational taxonomic units
microbial genomic sequencess clustered by sequence similarity
partition sequences into discrete groups instead of traditional taxonomic units.
the most abundant sequence in an OTU is the representative sequence
representative sequences from all the OTUs are used to construct a phylogenetic tree among all the OTUs
Microbial community information == OTUs + counts + phylogenetic relationship + taxonomy
Human gut microbiome study in University of Pennsylvania
the effect of diet on gut microbiome composition
- gut microbiome data
- nutrient intake data
distance based analysis
-
identify a few gut microbiome associated nutrients
-
unable to provide information on how dietary nutrient affect bacterial taxa
Goal
identify both the key nutrients as well as the taxa the nutrient affect
Chen and Li (2013) adopted a regression-based approach
OTU abundance data as multivariate count responses, and nutrient as covaraite
Model
Multinomial logistic regression
The link function is a multinomial-Poisson transformation
might need to use Poissonization to simulate the data
Overdisperson
-
the multinomial distribution is not appropriate
-
is a random variable with some prior distribution
-
is a (d-1) dimensional simplex,
-
the support of p is
-
Dirichlet distribution density at
-
Dirichlet is a conjugate prior to multinomial distribution
-
posterior is Dirichlet multionmial distribution, aka the Dirichlet compound multinomial distribution.
Limitation
-
all components must share a common variance parameter
-
components are mutually independent, up to the constraint that must sum up to 1
-
distribution fails to take into account the special and inherent property of microbiome count data (evolutionary relationships in the phylogenetic tree)
Generalization of Dirichlet Multinomial distribution
-
the relationships among the components of the count vector can be represented as a tree, node-by-node.
-
each component has a independent variance
-
components are correlated at subtree levels
-
-
a regression model with the effects of covariates
-
a regularized methods for selecting covarites (nutrients) that are associated with the count responses (OTUs)
Logistic Normal Multinomial distribution
-
Billheimer with Aitchison’s logistic normal distribution instead of Dirichlet
- covaraites to the count vector (Billheimer et al. 2001)
- link dietary nutrients with bacteria counts (Xia et al. 2013)
- cannot exploit the tree structure information, logistic normal multinomial does not have a closed-form expression.
Dirichlet-Tree Multinomial Distributions
-
total number of counts, determined by the sequence depth, as an ancillary statistics
- analysis conditioning on this number
-
A Tree
representing the hierarchical structure over the count responses
-
we will incorporate the tree structural information into the modeling
-
the set of leaf nodes
-
the set of internal nodes of
-
for each
,
the child nodes of
-
for each
and
,
-
-
-
-
-
is the index for the subtree counts and probabilities
-
Let
to be the root node of
.
-
each leaf node is
- the path from
to
, where
is the inner branches in this path
, with the
that each branch as a probability (a conditional probability given we know where the branch started).
- the path from
-
for
is the product of branch probabilities from root
to final leaf
-
this is for the leaf level
- this is for the internal nodes
the joint density of
has the form of:
-
-
is the number of children of
-
-
that each component in the product
corresponds to a interior node in the tree
-
the Dirichlet multinomial distribution based on the accumulated counts along branches of given node.
-
given
- when
, each
has an independent variance
- two components
with in the same subtree indexed by
are correlated, due to the same ancestor of
.
- when
Dirichlet Tree Multinomial Regression Model
-
a regression of
on
covariates
-
for each
and
we express
as a linear combination of the covariates.
Regularized Likelihood Estimation
-
parametrization for Dirichlet Tree Multinomial Regression Model
-
the number of
time the number of tree branches
Algorithm of accelerated proximal gradient method
-
approximate
at
Add the following code to your website.
For more information on customizing the embed code, read Embedding Snippets.
