README.md

In JerryBubble/skeletonClus: Skeleton Clustering method

skeletonClus

Skeleton Clustering R package

skeletonClus is R package implementing the Skeleton Clustering methods in :

Zeyu Wei, and Yen-Chi Chen. "Skeleton Clustering: Dimension-Free Density-based Clustering." 2021.

The manuscript of the paper can be found at here.

The follwoing figure illustrates the overall procedure of the skeleton clustering method.

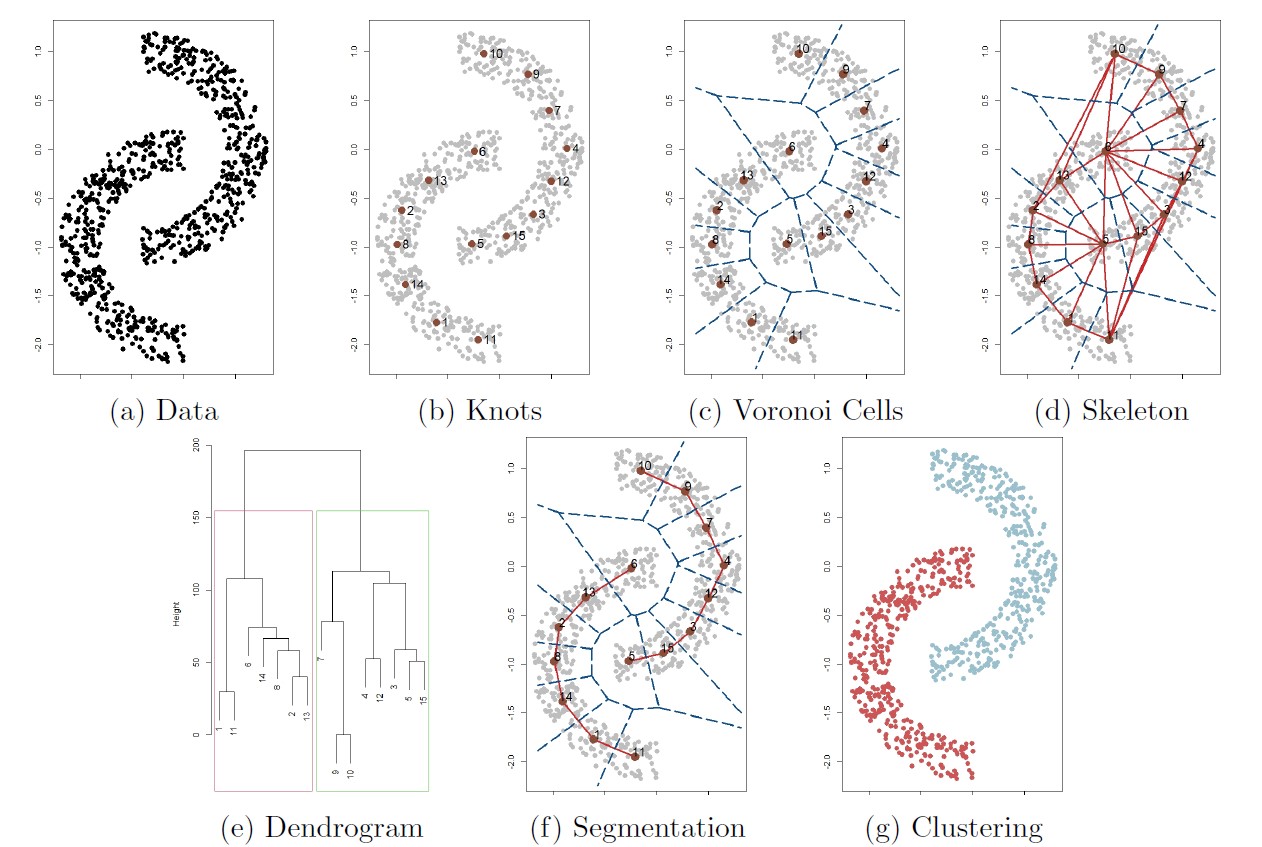
Starting with a collection of observations (panel (a)), we first find knots, the representative points of the entire data (panel (b)). By default we use the k-means algorithm to choose knots. Then we compute the corresponding Voronoi cells induced by the knots (panel (c)) and the edges associating the Voronoi cells (panel (d), this is the Delaunay triangulation). For each edge in the graph, we compute a density-based similarity measure that quantifies the closeness of each pair of knots. For the next step we segment knots into groups based on a linkage criterion (single linkage in this example), leading to the dendrogram in panel (e). Finally, we choose a threshold that cuts the dendrogram into $S = 2$ clusters (panel (f)) and assign cluster label to each observation according to the knot-cluster that it belongs to (panel (g)).

Installation

The package currently only exists on github. Installed directly from this repo with help from the devtools package. Run the following in R:

```R
install.packages("devtools")
devtools::install_github("JerryBubble/skeletonClus") 
```

Development note

The package is actively developing.

Usage

Load R-package and simulate Yinyang data of dimension 100

library("skeletonClus")

dat = Yinyang_data(d = 100)
X0 = dat$data
y0 = dat$clus

Other simulation data used in the skeleton clustering paper can be genereted similarly: Mickey_data() for Mickey data, MM_data() for Manifold Mixture data, MixMickey_data() for Mix Mickey data, MixStar_data() for mixture of three Gaussian cluster giving a star shape, and ring_data() for Ring data

Also, with set.seed(1234) the 1000-dimensional simulated datasets are also built into the skeletonClus package, with names Yinyang1000, Ring1000, Mickey1000, MixMickey1000, MixStar1000, ManifoldMix1000. Those built in datasets can be load into R working environment by

data(Yinyang1000)

We proceed with constructing the weighted skeleton with overfitting k-means, wihch can be donw with the skeletonCons function:

skeleton = skeletonCons(X0, rep = 1000)

For more flexible usage of skeletonCons see the help page at

?skeletonCons

The knots and the Voronoi density edge weights can be accessed as

skeleton$centers
skeleton$voron_weights

The Face density, Tube density, and Average Distance density weights can be accessed in similar fashion. We then segment the knots based on the edge weights with hierarchical clustering (taking Voronoi density for example):

##turn similarity into distance
VD_tmp = max(skeleton$voron_weights) - skeleton$voron_weights 
diag(VD_tmp) = 0
VD_tmp = as.dist(VD_tmp)

##perform hierarchical clustering on the distance matrix
VD_hclust = hclust(VD_tmp, method="single")

If the final number of clusters is unknown, we can plot the dendrogram of hierarchical clustering to see the structure of the data and pick a cutting threshold. Here we know the data have 5 components and hence we cut the tree into 5 groups.

##plot dendrogram
plot(VD_hclust)
##cut tree 
VD_lab = cutree(VD_hclust, k=5)

Then we assign the label of each observation to have the same group membership as the closest knot

X_lab_VD = VD_lab[skeleton$cluster]

With the mclust R package we can calculate the adjusted Rand index:

library("mclust")
voron_rand = adjustedRandIndex(X_lab_VD, y0)

FInally we can get a plot to visualize the clustering result:

 plot(X0[,1], X0[,2], col = cols[X_lab_VD], main = "Skeleton Clustering with Voronoi Density", xlab = "X", ylab = "Y", cex.main=1.5)

JerryBubble/skeletonClus documentation built on Dec. 18, 2021, 1:28 a.m.