README.md

In RobinHankin/elliptic: Weierstrass and Jacobi Elliptic Functions

The elliptic package: Weierstrass and Jacobi elliptic functions in R

Overview

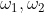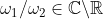An elliptic function is a meromorphic complex function that is periodic in two directions. That is, there exist two nonzero complex numbers with such that

whenever 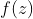is defined; note carefully the factors of 2. There are two natural ways of presenting elliptic functions: that of Weierstrass, and that of Jacobi. Historically, the Jacobi form was first presented and is the most practically useful, but the Weierstrass form is more elegant (IMO).

Terminology follows that of Abramowitz and Stegun wherever possible.

Installation

To install the most recent stable version on CRAN, use install.packages() at the R prompt:

R> install.packages("elliptic")

To install the current development version use devtools:

R> devtools::install_github("RobinHankin/elliptic")

And then to load the package use library():

library("elliptic")

The package comes with an extensive and detailed vignette; type vignette("elliptic") at the R commandline.

The package in use

The Weierstrass elliptic function is evaluated numerically by P(), which takes the half period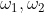s . Thus

z <- 0.3 + 0.2i
omega1 <- 5+1i; omega2 <- 1+7i  # half-periods
f <- function(z){P(z,Omega=c(omega1,omega2))}
c(f(z),f(z + 10+2i), f(z + 2+14i))  # should be equal

## [1] 2.958647-7.100563i 2.958647-7.100563i 2.958647-7.100563i

The elliptic functions can be visualised using view():

x <- seq(from=-4, to=4, len=200)
y <- x
z <- outer(x,1i*x, "+")
f <- P(z, c(1+1i,2-3i))
par(pty="s")
view(x,y,f,real.contour=FALSE,drawlabel=FALSE,axes=FALSE,xlab="Re(z)",ylab="Im(z)", main="P(z,1+i,2-3i)")
axis(1,pos = -4)
axis(2,pos = -4)
lines(x=c(-4,4),y=c(4,4))
lines(y=c(-4,4),x=c(4,4))

Related functions include 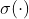(sigma() and the 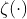(zeta()).

Jacobi forms

Jacobi’s elliptic functions are implemented in the package with their standard names sn(), cn(), dn() etc. For example:

view(x,y,sn(z,m=6),real=FALSE,drawlabel=FALSE,axes=FALSE,xlab="Re(z)",ylab="Im(z)", main="The Jacobi sn() function")
axis(1,pos = -4,at=c(-4,-2,0,2,4))
axis(2,pos = -4,at=c(-4,-2,0,2,4))
lines(x=c(-4,4),y=c(4,4))
lines(y=c(-4,4),x=c(4,4))

The Jacobi forms are useful in physics and we can use them to visualise potential flow in a rectangle:

n <- 300
K <- K.fun(1/2)  # aspect ratio
f <- function(z){1i*log((z-1.7+3i)*(z-1.7-3i)/(z+1-0.3i)/(z+1+0.3i))} # position of source and sink
x <- seq(from=-K,to=K,len=n)
y <- seq(from=0,to=K,len=n)
z <- outer(x,1i*y,"+")

view(x, y, f(sn(z,m=1/2)), nlevels=44, real.contour=TRUE, drawlabels=FALSE,
     main="Potential flow in a rectangle",axes=FALSE,xlab="",ylab="")
rect(-K,0,K,K,lwd=3)

References

• M Abramowitz and IA Stegun (1965). Handbook of Mathematical Functions. New York: Dover
• RKS Hankin (2006). “Introducing elliptic, an R package for elliptic and modular functions”. Journal of Statistical Software, 15:7
• K Chandrasekharan (1985). Elliptic functions. Springer-Verlag

RobinHankin/elliptic documentation built on June 10, 2025, 1:45 a.m.