README.md

In Robinlovelace/si: Flexible Framework for Developing Spatial Interaction Models

The goal of {simodels} is to provide a simple, tidy, and flexible framework for developing spatial interaction models (SIMs). SIMs estimate the amount of movement between spatial entities and can be used for many things, including to support evidence-based investment in sustainable transport infrastructure and prioritisation of location options for public services.

Unlike many software tools designed to support spatial interaction modelling, {simodels} does not define (or even encourage use of) any particular functional forms or modelling frameworks for predicting movement between origins and destinations. Instead, it provides a framework enabling you to use model function forms or models of your choosing, ensuring flexibility and encouraging flexibility.

Installation

Install the package as follows:

install.packages("remotes") # if not already installed

remotes::install_github("robinlovelace/simodels")

To get the develoment version do:

devtools::load_all()

simodel basics

Run a basic SIM as follows:

library(simodels)
library(dplyr)
# prepare OD data
od = si_to_od(
  origins = si_zones,        # origin locations
  destinations = si_zones,   # destination locations
  max_dist = 5000            # maximum distance between OD pairs
  )
# specify a function
gravity_model = function(beta, d, m, n) {
  m * n * exp(-beta * d / 1000)
} 
# perform SIM
od_res = si_calculate(
  od,
  fun = gravity_model,
  d = distance_euclidean,
  m = origin_all,
  n = destination_all,
  constraint_production = origin_all,
  beta = 0.9
  )
# visualize the results
plot(od_res$distance_euclidean, od_res$interaction)

What just happened? We created an ‘OD data frame’ with the function si_to_od() from geographic origins and destinations, and then estimated a simple ‘production constrained’ (with the constraint_production argument) gravity model based on the population in origin and destination zones and a custom distance decay function with si_calculate(). As the example above shows, the package allows/encourages you to define and use your own functions to estimate the amount of interaction/movement between places.

The approach is also ‘tidy’, allowing use of {simodels} functions in {dplyr} pipelines:

od_res = od %>% 
  si_calculate(fun = gravity_model, 
               m = origin_all,
               n = destination_all,
               d = distance_euclidean,
               constraint_production = origin_all,
               beta = 0.3)
od_res %>% 
  select(interaction)

Simple feature collection with 2505 features and 1 field
Geometry type: LINESTRING
Dimension:     XY
Bounding box:  xmin: -1.743949 ymin: 53.71552 xmax: -1.337493 ymax: 53.92906
Geodetic CRS:  WGS 84
# A tibble: 2,505 × 2
   interaction                                 geometry
         <dbl>                         <LINESTRING [°]>
 1       2177. (-1.400108 53.92906, -1.400108 53.92906)
 2        632. (-1.400108 53.92906, -1.346497 53.92305)
 3        556. (-1.346497 53.92305, -1.400108 53.92906)
 4       1382. (-1.346497 53.92305, -1.346497 53.92305)
 5        449. (-1.346497 53.92305, -1.357667 53.88306)
 6        794. (-1.704658 53.91073, -1.704658 53.91073)
 7        749.   (-1.704658 53.91073, -1.6876 53.90066)
 8        287. (-1.704658 53.91073, -1.743949 53.88035)
 9        267. (-1.704658 53.91073, -1.710657 53.87087)
10        186. (-1.704658 53.91073, -1.694076 53.86729)
# ℹ 2,495 more rows

The resulting estimates of interaction, returned in the column interaction and plotted with distance in the graphic above, resulted from our choice of spatial interaction model inputs, allowing a wide range of alternative approaches to be implemented. This flexibility is a key aspect of the package, enabling small and easily modified functions to be implemented and tested.

The output of si_calculate() is a geographic object that can be plotted with sf’s plot method (or other geographic data visualisation packages):

plot(od_res["interaction"], logz = TRUE)

The si_to_od() function transforms geographic entities (typically polygons and points) into a data frame representing the full combination of origin-destination pairs that are less than max_dist meters apart. A common saying in data science is that 80% of the effort goes into the pre-processing stage. This is equally true for spatial interaction modelling as it is for other types of data intensive analysis/modelling work. So what does this function return?

The function allows you to use any variable in the origin or destination data by joining all attributes onto the OD data frame, with column names appended with origin and destination.

The approach works equally well for ‘bipartite’ SIMs, in which origin and destination points are different (Hasova et al. 2022). The following example implements a bipartite SIM that estimates the number of trips from administrative zones to pubs in Leeds:

# Set n. trips to pubs, assuming that for every trip to the pub there are
# 50 trips to work (this would be validated/tested/modelled in empirical work)
zones_pubs = si_zones %>% 
  mutate(to_pubs = all / 50)
pubs_example = si_pubs %>% 
  filter(grepl(pattern = "Chemic|Nag", x = name))
pubs_example$size = c(100, 80)
od_to_pubs = si_to_od(zones_pubs, pubs_example)
od_to_pubs_result = od_to_pubs %>% 
  si_calculate(fun = gravity_model, 
               m = origin_to_pubs,
               n = destination_size,
               d = distance_euclidean,
               beta = 0.5,
               constraint_production = origin_to_pubs)
od_to_pubs_result %>% 
  select(O, D, destination_name, interaction)

Simple feature collection with 214 features and 4 fields
Geometry type: LINESTRING
Dimension:     XY
Bounding box:  xmin: -1.743949 ymin: 53.71552 xmax: -1.337493 ymax: 53.92906
Geodetic CRS:  WGS 84
# A tibble: 214 × 5
   O         D         destination_name  interaction                    geometry
   <chr>     <chr>     <chr>                   <dbl>            <LINESTRING [°]>
 1 E02002330 127960333 The Chemic Tavern        18.4 (-1.400108 53.92906, -1.55…
 2 E02002331 127960333 The Chemic Tavern        15.9 (-1.346497 53.92305, -1.55…
 3 E02002332 127960333 The Chemic Tavern        25.5 (-1.704658 53.91073, -1.55…
 4 E02002333 127960333 The Chemic Tavern        38.7 (-1.6876 53.90066, -1.5528…
 5 E02002334 127960333 The Chemic Tavern        20.9 (-1.357667 53.88306, -1.55…
 6 E02002335 127960333 The Chemic Tavern        19.9 (-1.470966 53.89184, -1.55…
 7 E02002336 127960333 The Chemic Tavern        25.5 (-1.624775 53.88589, -1.55…
 8 E02002337 127960333 The Chemic Tavern        37.2 (-1.743949 53.88035, -1.55…
 9 E02002338 127960333 The Chemic Tavern        36.8 (-1.710657 53.87087, -1.55…
10 E02002339 127960333 The Chemic Tavern        29.0 (-1.694076 53.86729, -1.55…
# ℹ 204 more rows

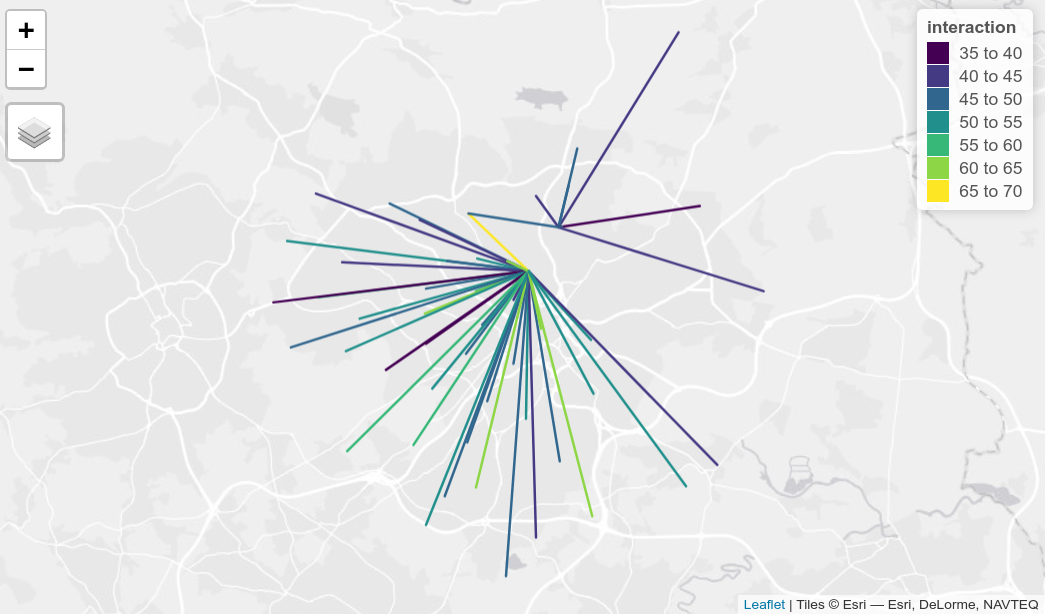
We can plot the top 20 desire lines between zone centroids and the 2 pubs in the example dataset as follows:

library(tmap)
tmap_mode("view")
od_to_pubs_result %>% 
  top_n(n = 50, wt = interaction) %>% 
  tm_shape() +
  tm_lines(col = "interaction", palette = "viridis", scale = 2)

Feedback

We would be interested to hear how the approach presented in this package compared with other implementations such as those presented in the links below. If anyone would like to try the approach or implement it in another language feel free to get in touch via the issue tracker.

Further reading

For details on what SIMs are and how they have been defined mathematically and in code from first principles, see the sims vignette.

To dive straight into using {simodels} to develop SIMs, see the Get started vignette.

For a detailed introduction to SIMs, support by reproducible R code, see Adam Dennett’s 2018 paper.

Other SIM packages

• The spflow R package
• The spint Python package
• The gravity R package
• The mobility R package
• The gravity functions in the scikit-mobility Python package

Robinlovelace/si documentation built on Sept. 28, 2024, 10:41 a.m.