README.md
In a-chernofsky/project2: Thesis project 2: causal mediation analysis with an interval censored outcome
knitr::opts_chunk$set(
collapse = TRUE,
comment = "#>",
fig.path = "man/figures/README-",
out.width = "100%"
)
set.seed(1233)
Project 2
The goal of project2 is to to estimate the indirect and direct effects
of a treatment A on a time-to-event outcome T with a mediator M, when T
is interval censored. The primary purpose of the package is to provide
functions for estimating the indirect and direct effects from data. A
secondary goal is to provide functions to conduct a simulation study to
evaluate the proposed estimators. We deomonstrate the simulation
functionality of the package below.
Installation
You can install the released version of project2 from the development
version from GitHub with:
# install.packages("devtools")
devtools::install_github("a-chernofsky/project2")
Prerequisites
library(survival)
library(interval)
#> Loading required package: perm
#> Loading required package: Icens
#> Loading required package: MLEcens
#> Depends on Icens package available on bioconductor.
#> To install use for example:
#> install.packages('BiocManager')
#> BiocManager::install('Icens')
library(project2)
Overview
- Simulate time-to-event outcomes conditional on covariates using
sim_cph with the following arguments:
N simulated sample sizeformula or X defining the covariatesbeta covariate effects tfun time function based on the assumed hazard function
- Create interval censored outcome based on when the simulated
time-to-event occurs with
sim_interval and the following
arguments:
t true event timespmiss probability of missingvisits a vector of study visit times
- Define a study visit schedule mimicking one way in which interval
censored outcomes arise.
- Recognizing that subjects miss study visits, set a probability of a
subject missing a specific visit.
Simulating Cox Proportional Hazards model data
Bender 2005 discussed a method to simulate time-to-event data from a Cox
Proportional Hazards model with hazard function based on the probability
integral transformation theorem. The method involves inverting the
cumulative hazard function. While the method is generalized to any
hazard function, choosing from popular survival distributions such as
exponential, weibull, and gompertz provides a closed form inverse
function that is simple to define. The sim_cph currently has functions
to simulate survival times from these common distributions.
The sim_cph function takes the following arguments:
N simulated sample sizeformula or X defining the covariatesbeta covariate effects tfun time function based on the assumed hazard.
Assume the following CPH model with a constant baseline hazard function
:
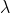The variables
are simulated from the following distributions:
#simulate covariates
x1 <- rbinom(100, 1, 0.5)
x2 <- rnorm(100)
x3 <- factor(sample(c(1,2,3), size = 100, replace = T, prob = c(0.33, 0.33, 0.33)))
We now set the values for the
,
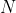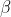’s and
,
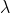#N
n <- 100
#betas
b <- c(-0.5, -0.02, 0.01, 0.01)
#lambda
lam <- 0.1
There are two ways to input the covariates into sim_cph: 1. X as a
model matrix (use model.matrix function) 2. formula as a formula
e.g. ~x1 + x2 + x3.
Make sure that any categorical variables are converted as factors
otherwise they will be treated as numeric.
t_data <- sim_cph(N = n, formula = ~ x1 + x2 + x3,
beta = b,
tfun = texp(lam))
We can use functions from the survival package to inspect the simulated
data:
t_data$event <- 1
sfit <- survfit(Surv(t, event) ~ x1, data = t_data)
summary(sfit)
#> Call: survfit(formula = Surv(t, event) ~ x1, data = t_data)
#>
#> x1=0
#> time n.risk n.event survival std.err lower 95% CI upper 95% CI
#> 0.215 59 1 0.9831 0.0168 0.95066 1.000
#> 0.321 58 1 0.9661 0.0236 0.92101 1.000
#> 0.441 57 1 0.9492 0.0286 0.89472 1.000
#> 0.951 56 1 0.9322 0.0327 0.87021 0.999
#> 1.086 55 1 0.9153 0.0363 0.84688 0.989
#> 1.389 54 1 0.8983 0.0393 0.82440 0.979
#> 1.684 53 1 0.8814 0.0421 0.80259 0.968
#> 1.979 52 1 0.8644 0.0446 0.78132 0.956
#> 2.088 51 1 0.8475 0.0468 0.76051 0.944
#> 2.323 50 1 0.8305 0.0488 0.74009 0.932
#> 2.536 49 1 0.8136 0.0507 0.72001 0.919
#> 2.885 48 1 0.7966 0.0524 0.70025 0.906
#> 2.908 47 1 0.7797 0.0540 0.68076 0.893
#> 2.968 46 1 0.7627 0.0554 0.66153 0.879
#> 3.672 45 1 0.7458 0.0567 0.64254 0.866
#> 3.708 44 1 0.7288 0.0579 0.62376 0.852
#> 3.945 43 1 0.7119 0.0590 0.60519 0.837
#> 4.032 42 1 0.6949 0.0599 0.58682 0.823
#> 4.503 41 1 0.6780 0.0608 0.56863 0.808
#> 4.654 40 1 0.6610 0.0616 0.55062 0.794
#> 5.050 39 1 0.6441 0.0623 0.53278 0.779
#> 5.179 38 1 0.6271 0.0630 0.51511 0.763
#> 5.281 37 1 0.6102 0.0635 0.49759 0.748
#> 5.655 36 1 0.5932 0.0640 0.48023 0.733
#> 5.873 35 1 0.5763 0.0643 0.46302 0.717
#> 6.520 34 1 0.5593 0.0646 0.44596 0.701
#> 6.794 33 1 0.5424 0.0649 0.42905 0.686
#> 6.801 32 1 0.5254 0.0650 0.41228 0.670
#> 6.895 31 1 0.5085 0.0651 0.39565 0.653
#> 6.897 30 1 0.4915 0.0651 0.37917 0.637
#> 7.795 29 1 0.4746 0.0650 0.36283 0.621
#> 8.100 28 1 0.4576 0.0649 0.34663 0.604
#> 8.104 27 1 0.4407 0.0646 0.33058 0.587
#> 8.193 26 1 0.4237 0.0643 0.31467 0.571
#> 8.294 25 1 0.4068 0.0640 0.29891 0.554
#> 9.296 24 1 0.3898 0.0635 0.28329 0.536
#> 11.022 23 1 0.3729 0.0630 0.26783 0.519
#> 11.058 22 1 0.3559 0.0623 0.25252 0.502
#> 11.086 21 1 0.3390 0.0616 0.23737 0.484
#> 11.294 20 1 0.3220 0.0608 0.22239 0.466
#> 11.486 19 1 0.3051 0.0599 0.20757 0.448
#> 11.584 18 1 0.2881 0.0590 0.19294 0.430
#> 12.427 17 1 0.2712 0.0579 0.17848 0.412
#> 12.493 16 1 0.2542 0.0567 0.16423 0.394
#> 12.572 15 1 0.2373 0.0554 0.15018 0.375
#> 13.467 14 1 0.2203 0.0540 0.13634 0.356
#> 13.860 13 1 0.2034 0.0524 0.12275 0.337
#> 15.450 12 1 0.1864 0.0507 0.10941 0.318
#> 15.872 11 1 0.1695 0.0488 0.09635 0.298
#> 16.515 10 1 0.1525 0.0468 0.08360 0.278
#> 18.622 9 1 0.1356 0.0446 0.07119 0.258
#> 18.830 8 1 0.1186 0.0421 0.05918 0.238
#> 19.597 7 1 0.1017 0.0393 0.04764 0.217
#> 21.240 6 1 0.0847 0.0363 0.03664 0.196
#> 29.778 5 1 0.0678 0.0327 0.02632 0.175
#> 32.881 4 1 0.0508 0.0286 0.01688 0.153
#> 34.979 3 1 0.0339 0.0236 0.00868 0.132
#> 45.810 2 1 0.0169 0.0168 0.00243 0.118
#> 50.517 1 1 0.0000 NaN NA NA
#>
#> x1=1
#> time n.risk n.event survival std.err lower 95% CI upper 95% CI
#> 0.777 41 1 0.9756 0.0241 0.92952 1.000
#> 1.155 40 1 0.9512 0.0336 0.88752 1.000
#> 1.181 39 1 0.9268 0.0407 0.85045 1.000
#> 1.489 38 1 0.9024 0.0463 0.81604 0.998
#> 2.514 37 1 0.8780 0.0511 0.78339 0.984
#> 2.913 36 1 0.8537 0.0552 0.75204 0.969
#> 2.919 35 1 0.8293 0.0588 0.72173 0.953
#> 4.047 34 1 0.8049 0.0619 0.69227 0.936
#> 4.469 33 1 0.7805 0.0646 0.66354 0.918
#> 4.928 32 1 0.7561 0.0671 0.63544 0.900
#> 5.971 31 1 0.7317 0.0692 0.60791 0.881
#> 6.949 30 1 0.7073 0.0711 0.58090 0.861
#> 7.005 29 1 0.6829 0.0727 0.55436 0.841
#> 8.777 28 1 0.6585 0.0741 0.52827 0.821
#> 9.610 27 1 0.6341 0.0752 0.50259 0.800
#> 9.696 26 1 0.6098 0.0762 0.47732 0.779
#> 9.882 25 1 0.5854 0.0769 0.45242 0.757
#> 10.748 24 1 0.5610 0.0775 0.42790 0.735
#> 11.598 23 1 0.5366 0.0779 0.40374 0.713
#> 12.493 22 1 0.5122 0.0781 0.37993 0.691
#> 12.841 21 1 0.4878 0.0781 0.35647 0.668
#> 13.449 20 1 0.4634 0.0779 0.33337 0.644
#> 14.151 19 1 0.4390 0.0775 0.31061 0.621
#> 15.694 18 1 0.4146 0.0769 0.28821 0.597
#> 16.200 17 1 0.3902 0.0762 0.26617 0.572
#> 16.374 16 1 0.3659 0.0752 0.24451 0.547
#> 17.711 15 1 0.3415 0.0741 0.22322 0.522
#> 17.762 14 1 0.3171 0.0727 0.20233 0.497
#> 17.994 13 1 0.2927 0.0711 0.18186 0.471
#> 20.465 12 1 0.2683 0.0692 0.16184 0.445
#> 21.162 11 1 0.2439 0.0671 0.14229 0.418
#> 23.361 10 1 0.2195 0.0646 0.12325 0.391
#> 23.496 9 1 0.1951 0.0619 0.10479 0.363
#> 37.418 8 1 0.1707 0.0588 0.08696 0.335
#> 40.751 7 1 0.1463 0.0552 0.06987 0.307
#> 46.208 6 1 0.1220 0.0511 0.05364 0.277
#> 47.107 5 1 0.0976 0.0463 0.03846 0.248
#> 51.568 4 1 0.0732 0.0407 0.02462 0.217
#> 64.462 3 1 0.0488 0.0336 0.01262 0.188
#> 73.976 2 1 0.0244 0.0241 0.00352 0.169
#> 83.617 1 1 0.0000 NaN NA NA
plot(sfit, col = c("red", "blue"))
We can fit a CPH model to check the results:
coxph(Surv(t, event) ~ x1 + x2 + x3, data = t_data)
#> Call:
#> coxph(formula = Surv(t, event) ~ x1 + x2 + x3, data = t_data)
#>
#> coef exp(coef) se(coef) z p
#> x1 -0.6244 0.5356 0.2196 -2.843 0.00447
#> x2 -0.0334 0.9672 0.1048 -0.319 0.75010
#> x32 0.1216 1.1293 0.2448 0.497 0.61938
#> x33 0.4598 1.5837 0.2661 1.728 0.08400
#>
#> Likelihood ratio test=11.9 on 4 df, p=0.01815
#> n= 100, number of events= 100
Simulating interval censored data
int_data <- sim_interval(t_data$t, pmiss = 0.10, visits = c(0, 1, 5, 10, 15, 20))
icfit <- icfit(Surv(l, r, type = "interval2") ~ x1, data = int_data)
plot(icfit, XLEG = 15, YLEG = 0.8, shade = F)
Calculating RMST with right censored data
i1 <- summary(sfit)$strata == "x1=1"
i0 <- summary(sfit)$strata == "x1=0"
t1 <- summary(sfit)$time[i1]
s1 <- summary(sfit)$surv[i1]
t0 <- summary(sfit)$time[i0]
s0 <- summary(sfit)$surv[i0]
Calculating RMST with interval censored data
rmst_ic(left = int_data$l[t_data$x1 == 1],
right = int_data$r[t_data$x1 == 1],
tau = 20)
#> [1] 12.21392
rmst_ic(left = int_data$l[t_data$x1 == 0],
right = int_data$r[t_data$x1 == 0],
tau = 20)
#> [1] 9.256934
Pseudo-observations
a-chernofsky/project2 documentation built on Oct. 21, 2021, 10:23 p.m.
R Package Documentation
Browse R Packages
We want your feedback!
Note that we can't provide technical support on individual packages. You should contact the package authors for that.
knitr::opts_chunk$set(
collapse = TRUE,
comment = "#>",
fig.path = "man/figures/README-",
out.width = "100%"
)
set.seed(1233)
Project 2
The goal of project2 is to to estimate the indirect and direct effects of a treatment A on a time-to-event outcome T with a mediator M, when T is interval censored. The primary purpose of the package is to provide functions for estimating the indirect and direct effects from data. A secondary goal is to provide functions to conduct a simulation study to evaluate the proposed estimators. We deomonstrate the simulation functionality of the package below.
Installation
You can install the released version of project2 from the development version from GitHub with:
# install.packages("devtools")
devtools::install_github("a-chernofsky/project2")
Prerequisites
library(survival)
library(interval)
#> Loading required package: perm
#> Loading required package: Icens
#> Loading required package: MLEcens
#> Depends on Icens package available on bioconductor.
#> To install use for example:
#> install.packages('BiocManager')
#> BiocManager::install('Icens')
library(project2)
Overview
- Simulate time-to-event outcomes conditional on covariates using
sim_cphwith the following arguments:Nsimulated sample sizeformulaorXdefining the covariatesbetacovariate effectstfuntime function based on the assumed hazard function
- Create interval censored outcome based on when the simulated
time-to-event occurs with
sim_intervaland the following arguments:ttrue event timespmissprobability of missingvisitsa vector of study visit times
- Define a study visit schedule mimicking one way in which interval censored outcomes arise.
- Recognizing that subjects miss study visits, set a probability of a subject missing a specific visit.
Simulating Cox Proportional Hazards model data
Bender 2005 discussed a method to simulate time-to-event data from a Cox
Proportional Hazards model with hazard function based on the probability
integral transformation theorem. The method involves inverting the
cumulative hazard function. While the method is generalized to any
hazard function, choosing from popular survival distributions such as
exponential, weibull, and gompertz provides a closed form inverse
function that is simple to define. The sim_cph currently has functions
to simulate survival times from these common distributions.
The sim_cph function takes the following arguments:
Nsimulated sample sizeformulaorXdefining the covariatesbetacovariate effectstfuntime function based on the assumed hazard.
Assume the following CPH model with a constant baseline hazard function
:
The variables
are simulated from the following distributions:
#simulate covariates
x1 <- rbinom(100, 1, 0.5)
x2 <- rnorm(100)
x3 <- factor(sample(c(1,2,3), size = 100, replace = T, prob = c(0.33, 0.33, 0.33)))
We now set the values for the
,
’s and
,
#N
n <- 100
#betas
b <- c(-0.5, -0.02, 0.01, 0.01)
#lambda
lam <- 0.1
There are two ways to input the covariates into sim_cph: 1. X as a
model matrix (use model.matrix function) 2. formula as a formula
e.g. ~x1 + x2 + x3.
Make sure that any categorical variables are converted as factors otherwise they will be treated as numeric.
t_data <- sim_cph(N = n, formula = ~ x1 + x2 + x3,
beta = b,
tfun = texp(lam))
We can use functions from the survival package to inspect the simulated data:
t_data$event <- 1
sfit <- survfit(Surv(t, event) ~ x1, data = t_data)
summary(sfit)
#> Call: survfit(formula = Surv(t, event) ~ x1, data = t_data)
#>
#> x1=0
#> time n.risk n.event survival std.err lower 95% CI upper 95% CI
#> 0.215 59 1 0.9831 0.0168 0.95066 1.000
#> 0.321 58 1 0.9661 0.0236 0.92101 1.000
#> 0.441 57 1 0.9492 0.0286 0.89472 1.000
#> 0.951 56 1 0.9322 0.0327 0.87021 0.999
#> 1.086 55 1 0.9153 0.0363 0.84688 0.989
#> 1.389 54 1 0.8983 0.0393 0.82440 0.979
#> 1.684 53 1 0.8814 0.0421 0.80259 0.968
#> 1.979 52 1 0.8644 0.0446 0.78132 0.956
#> 2.088 51 1 0.8475 0.0468 0.76051 0.944
#> 2.323 50 1 0.8305 0.0488 0.74009 0.932
#> 2.536 49 1 0.8136 0.0507 0.72001 0.919
#> 2.885 48 1 0.7966 0.0524 0.70025 0.906
#> 2.908 47 1 0.7797 0.0540 0.68076 0.893
#> 2.968 46 1 0.7627 0.0554 0.66153 0.879
#> 3.672 45 1 0.7458 0.0567 0.64254 0.866
#> 3.708 44 1 0.7288 0.0579 0.62376 0.852
#> 3.945 43 1 0.7119 0.0590 0.60519 0.837
#> 4.032 42 1 0.6949 0.0599 0.58682 0.823
#> 4.503 41 1 0.6780 0.0608 0.56863 0.808
#> 4.654 40 1 0.6610 0.0616 0.55062 0.794
#> 5.050 39 1 0.6441 0.0623 0.53278 0.779
#> 5.179 38 1 0.6271 0.0630 0.51511 0.763
#> 5.281 37 1 0.6102 0.0635 0.49759 0.748
#> 5.655 36 1 0.5932 0.0640 0.48023 0.733
#> 5.873 35 1 0.5763 0.0643 0.46302 0.717
#> 6.520 34 1 0.5593 0.0646 0.44596 0.701
#> 6.794 33 1 0.5424 0.0649 0.42905 0.686
#> 6.801 32 1 0.5254 0.0650 0.41228 0.670
#> 6.895 31 1 0.5085 0.0651 0.39565 0.653
#> 6.897 30 1 0.4915 0.0651 0.37917 0.637
#> 7.795 29 1 0.4746 0.0650 0.36283 0.621
#> 8.100 28 1 0.4576 0.0649 0.34663 0.604
#> 8.104 27 1 0.4407 0.0646 0.33058 0.587
#> 8.193 26 1 0.4237 0.0643 0.31467 0.571
#> 8.294 25 1 0.4068 0.0640 0.29891 0.554
#> 9.296 24 1 0.3898 0.0635 0.28329 0.536
#> 11.022 23 1 0.3729 0.0630 0.26783 0.519
#> 11.058 22 1 0.3559 0.0623 0.25252 0.502
#> 11.086 21 1 0.3390 0.0616 0.23737 0.484
#> 11.294 20 1 0.3220 0.0608 0.22239 0.466
#> 11.486 19 1 0.3051 0.0599 0.20757 0.448
#> 11.584 18 1 0.2881 0.0590 0.19294 0.430
#> 12.427 17 1 0.2712 0.0579 0.17848 0.412
#> 12.493 16 1 0.2542 0.0567 0.16423 0.394
#> 12.572 15 1 0.2373 0.0554 0.15018 0.375
#> 13.467 14 1 0.2203 0.0540 0.13634 0.356
#> 13.860 13 1 0.2034 0.0524 0.12275 0.337
#> 15.450 12 1 0.1864 0.0507 0.10941 0.318
#> 15.872 11 1 0.1695 0.0488 0.09635 0.298
#> 16.515 10 1 0.1525 0.0468 0.08360 0.278
#> 18.622 9 1 0.1356 0.0446 0.07119 0.258
#> 18.830 8 1 0.1186 0.0421 0.05918 0.238
#> 19.597 7 1 0.1017 0.0393 0.04764 0.217
#> 21.240 6 1 0.0847 0.0363 0.03664 0.196
#> 29.778 5 1 0.0678 0.0327 0.02632 0.175
#> 32.881 4 1 0.0508 0.0286 0.01688 0.153
#> 34.979 3 1 0.0339 0.0236 0.00868 0.132
#> 45.810 2 1 0.0169 0.0168 0.00243 0.118
#> 50.517 1 1 0.0000 NaN NA NA
#>
#> x1=1
#> time n.risk n.event survival std.err lower 95% CI upper 95% CI
#> 0.777 41 1 0.9756 0.0241 0.92952 1.000
#> 1.155 40 1 0.9512 0.0336 0.88752 1.000
#> 1.181 39 1 0.9268 0.0407 0.85045 1.000
#> 1.489 38 1 0.9024 0.0463 0.81604 0.998
#> 2.514 37 1 0.8780 0.0511 0.78339 0.984
#> 2.913 36 1 0.8537 0.0552 0.75204 0.969
#> 2.919 35 1 0.8293 0.0588 0.72173 0.953
#> 4.047 34 1 0.8049 0.0619 0.69227 0.936
#> 4.469 33 1 0.7805 0.0646 0.66354 0.918
#> 4.928 32 1 0.7561 0.0671 0.63544 0.900
#> 5.971 31 1 0.7317 0.0692 0.60791 0.881
#> 6.949 30 1 0.7073 0.0711 0.58090 0.861
#> 7.005 29 1 0.6829 0.0727 0.55436 0.841
#> 8.777 28 1 0.6585 0.0741 0.52827 0.821
#> 9.610 27 1 0.6341 0.0752 0.50259 0.800
#> 9.696 26 1 0.6098 0.0762 0.47732 0.779
#> 9.882 25 1 0.5854 0.0769 0.45242 0.757
#> 10.748 24 1 0.5610 0.0775 0.42790 0.735
#> 11.598 23 1 0.5366 0.0779 0.40374 0.713
#> 12.493 22 1 0.5122 0.0781 0.37993 0.691
#> 12.841 21 1 0.4878 0.0781 0.35647 0.668
#> 13.449 20 1 0.4634 0.0779 0.33337 0.644
#> 14.151 19 1 0.4390 0.0775 0.31061 0.621
#> 15.694 18 1 0.4146 0.0769 0.28821 0.597
#> 16.200 17 1 0.3902 0.0762 0.26617 0.572
#> 16.374 16 1 0.3659 0.0752 0.24451 0.547
#> 17.711 15 1 0.3415 0.0741 0.22322 0.522
#> 17.762 14 1 0.3171 0.0727 0.20233 0.497
#> 17.994 13 1 0.2927 0.0711 0.18186 0.471
#> 20.465 12 1 0.2683 0.0692 0.16184 0.445
#> 21.162 11 1 0.2439 0.0671 0.14229 0.418
#> 23.361 10 1 0.2195 0.0646 0.12325 0.391
#> 23.496 9 1 0.1951 0.0619 0.10479 0.363
#> 37.418 8 1 0.1707 0.0588 0.08696 0.335
#> 40.751 7 1 0.1463 0.0552 0.06987 0.307
#> 46.208 6 1 0.1220 0.0511 0.05364 0.277
#> 47.107 5 1 0.0976 0.0463 0.03846 0.248
#> 51.568 4 1 0.0732 0.0407 0.02462 0.217
#> 64.462 3 1 0.0488 0.0336 0.01262 0.188
#> 73.976 2 1 0.0244 0.0241 0.00352 0.169
#> 83.617 1 1 0.0000 NaN NA NA
plot(sfit, col = c("red", "blue"))
We can fit a CPH model to check the results:
coxph(Surv(t, event) ~ x1 + x2 + x3, data = t_data)
#> Call:
#> coxph(formula = Surv(t, event) ~ x1 + x2 + x3, data = t_data)
#>
#> coef exp(coef) se(coef) z p
#> x1 -0.6244 0.5356 0.2196 -2.843 0.00447
#> x2 -0.0334 0.9672 0.1048 -0.319 0.75010
#> x32 0.1216 1.1293 0.2448 0.497 0.61938
#> x33 0.4598 1.5837 0.2661 1.728 0.08400
#>
#> Likelihood ratio test=11.9 on 4 df, p=0.01815
#> n= 100, number of events= 100
Simulating interval censored data
int_data <- sim_interval(t_data$t, pmiss = 0.10, visits = c(0, 1, 5, 10, 15, 20))
icfit <- icfit(Surv(l, r, type = "interval2") ~ x1, data = int_data)
plot(icfit, XLEG = 15, YLEG = 0.8, shade = F)
Calculating RMST with right censored data
i1 <- summary(sfit)$strata == "x1=1"
i0 <- summary(sfit)$strata == "x1=0"
t1 <- summary(sfit)$time[i1]
s1 <- summary(sfit)$surv[i1]
t0 <- summary(sfit)$time[i0]
s0 <- summary(sfit)$surv[i0]
Calculating RMST with interval censored data
rmst_ic(left = int_data$l[t_data$x1 == 1],
right = int_data$r[t_data$x1 == 1],
tau = 20)
#> [1] 12.21392
rmst_ic(left = int_data$l[t_data$x1 == 0],
right = int_data$r[t_data$x1 == 0],
tau = 20)
#> [1] 9.256934
Pseudo-observations
R Package Documentation
Browse R Packages
We want your feedback!
Note that we can't provide technical support on individual packages. You should contact the package authors for that.
Embedding an R snippet on your website
Add the following code to your website.
For more information on customizing the embed code, read Embedding Snippets.