In chiyahn/rMSWITCHQuZhuo: R package for Markov-regime switching models

knitr::opts_chunk$set(echo = TRUE)
library(rMSWITCH)
library(normalregMix)

This vignette document provides an introduction to users who wish to use rMSWITCH package for estimation of Markov regime-switching models and statistical test of the number of regimes. More details can be found in using-rMSWITCH.pdf in our public repository.

Models

MSI models

Autoregressive markov regime-switching in intercept models with $M$ regimes and $s$ autoregressive terms (MSI(M)-AR(s)), also known as dynamic regime-switching models, can be represented by a discrete stochastic process $$ y_t = \mu_{x_t} + \sum_{j=1}^s \beta_{j, x_t} y_{t-j} + \sigma_{x_t} \epsilon_t $$ where $x_t \in {1, ..., M}$ is the regime at time $t$ and $\epsilon_t \sim N(0,1)$. The model can be modified slightly so that variance or (and) autoregressive coefficient(s) is uniform across regimes as well. We also assume that the changes in regime follow a Markov process; that is, there is a fixed probability of $p_{ij}$ across time to switch from $i$th regime in $t-1$th period to $j$th regime in $t$th period where $i, j \in {1, ..., M}$.

MSM models

Autoregressive markov regime-switching in mean models with $M$ regimes and $s$ autoregressive terms (MSM(M)-AR(s)), also known as Hamilton models, can be represented by a discrete stochastic process $$ y_t = \mu_{x_t} + \sum_{j=1}^s \beta_{j, x_t} (y_{t-j} - \mu_{x_{t-j}} )+ \sigma_{x_t} \epsilon_t $$ Note that in this case, estimation at $t$th period requires depends on both the regime at $t$th period and regimes from $t-1$ to $t-s$.

General hidden markov models without autoregression

rMSWITCH can be also used to estimate and test for the number of regimes of Markov regime-switching models without autoregressive terms. In this case, $t$th sample is generated by a process $$ y_t = \mu_{x_t} + \sigma_{x_t} \epsilon_t $$

Obtaining Estimates

In rMSWITCH, EstimateMSAR can be called to estimate various Markov regime-switching models. To estimate MSI(1)-AR(1) model, which is equivalent with AR(1) model, call the following lines:

gdp.growth <- read.csv("GDPC1GROWTH.csv")
s <- 1
model1 <- EstimateMSAR(y = gdp.growth$GDPC1GROWTH, # data
             M = 1, # the number of regimes
             s = s, # the number of autoregressive terms
             is.beta.switching = FALSE, # decides whether autoregressive term(s) is
                                        # switching across regimes
             is.sigma.switching = FALSE) # decides whether variance is 
                                         # switching across regimes
print(model1)

To estimate MSI(2)-AR(1) models, simply set M to 2.

model2 <- EstimateMSAR(y = gdp.growth$GDPC1GROWTH, # data
             M = 2, # the number of regimes
             s = s, # the number of autoregressive terms
             is.beta.switching = FALSE, # decides whether autoregressive term(s) is 
                                        # switching across regimes
             is.sigma.switching = TRUE) # decides whether variance is 
                                        # switching across regimes
print(model2)

To estimate MSM(2)-AR(1) models, set is.MSM parameter TRUE.

model2.MSM <- EstimateMSAR(y = gdp.growth$GDPC1GROWTH, # data
             M = 2, # the number of regimes
             s = s, # the number of autoregressive terms
             is.beta.switching = FALSE, # decides whether autoregressive term(s) is 
                                        # switching across regimes
             is.sigma.switching = TRUE, # decides whether variance is 
                                        # switching across regimes
             is.MSM = TRUE) # decides whether the model is regime-switching in mean.
print(model2.MSM)

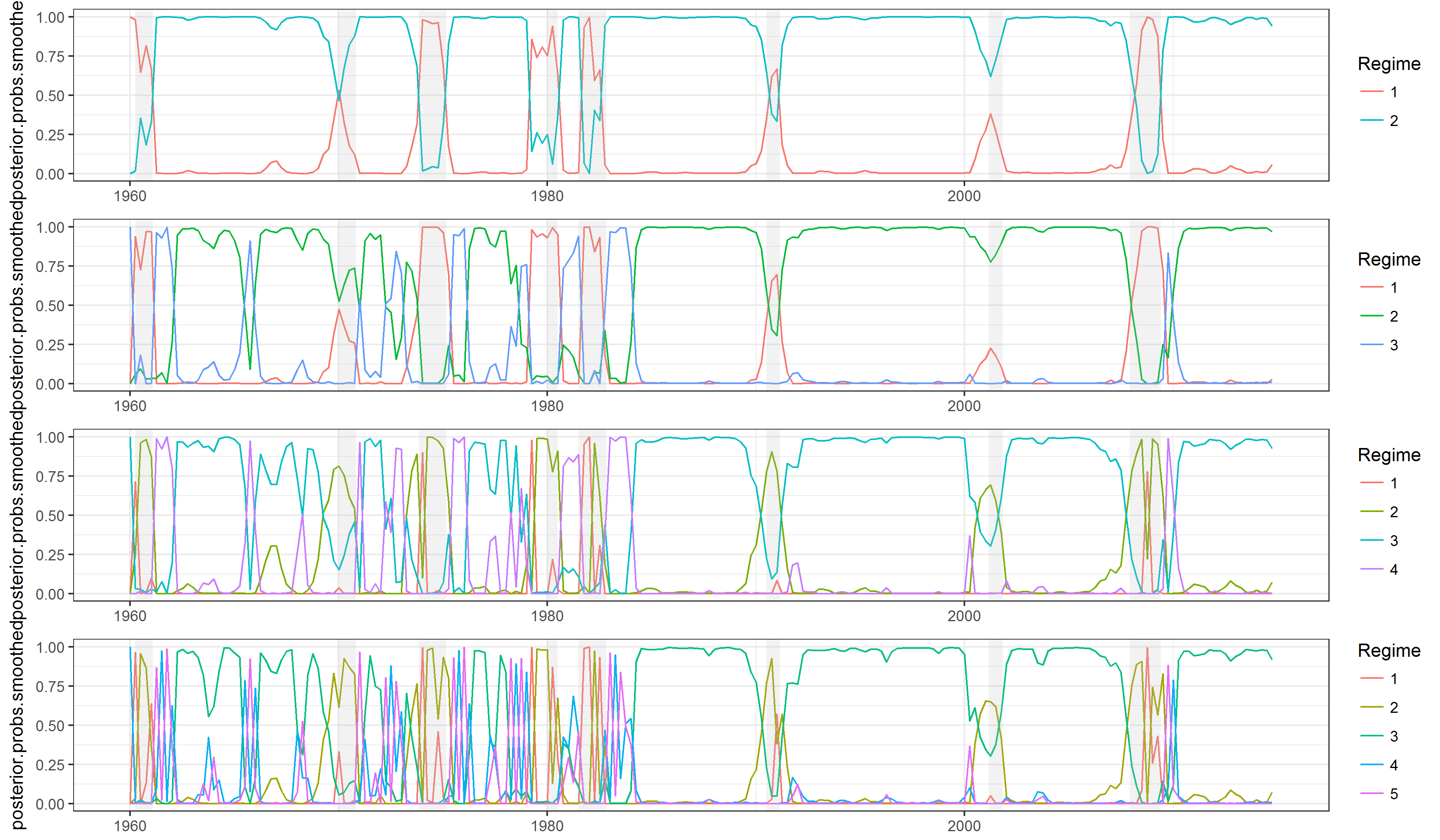
$Plots of posterior probability from estimated MSI(M)-AR(1), with a hard bound on switching probability $p_{ij} > 0.05$ for all $i,j \in {1,...,M}$.$

The posterior probability of $t$th state being in $j$th regime can be found by accessing posterior.probs.smoothed element of estimated models as well.

Testing the number of regimes

To test whether a hypothesis $H_0: M = 1$ against $H_1: M = 2$, i.e., a null hypothesis that the number of regimes is one, call TestMSAR as follows:

test1 <- TestMSAR(y = gdp.growth$GDPC1GROWTH, # data
             M = 1, # the number of regimes in a null hypothesis
             s = s, # the number of autoregressive terms
             is.beta.switching = FALSE, # decides whether autoregressive term(s) is
                                        # switching across regimes
             is.sigma.switching = FALSE) # decides whether variance is 
                                         # switching across regimes
print(test1)

which provides a $p-$value as well.

To repeat the procedure for $H_0: M = M_0$ for $M_0 = 1, 2, ..., \verb|max.M|$, simply call TestMSARSequence by setting max.M of your choice. For instance, to test hypotheses $H_0: M = M_0$ for $M_0 = 1, 2, 3$, call the following lines:

TestMSARSequence(y = gdp.growth$GDPC1GROWTH, # data
             max.M = 3, # the number of regimes in a null hypothesis
             s = s, # the number of autoregressive terms
             is.beta.switching = FALSE, # decides whether autoregressive term(s) is
                                        # switching across regimes
             is.sigma.switching = FALSE) # decides whether variance is 
                                         # switching across regimes