README.md

In deankoch/pkern: Fast Kriging with Product Kernels

pkern

an R package for modeling Gaussian processes on grids

Update October 2023

pkern is no longer in development. Last year, I rebranded it as snapKrig and released it on CRAN.

Head over to my snapKrig project page to get started.

Update June 2022

After some months of testing new ideas for improving this package I've committed a new version. This is a major update since the last commit - code files are reorganized more sensibly, and most functions have been rewritten and renamed. Nearly all of the package's functions now include test code and examples, and I am working on new vignettes.

A CRAN release is forthcoming. For now you can install the package using devtools and try out the Meuse River vignette.

Overview

pkern provides a computationally lean implementation of a 2-dimensional spatial correlation model for gridded data. This can be useful when working with geo-referenced data, such as in earth sciences, where users often need a tool for interpolation or down-scaling

More generally, pkern offers an fast and simple back-end for modeling with spatially correlated errors. It works much faster than alternatives like gstat, at the expense of somewhat restricting the type of model users can select.

pkern supports raster and geometry inputs from sf and terra, as well as simpler matrix and vector inputs. These two packages are suggested, but not required. pkern is written using only base dependencies (included by default in R) like graphics and stats.

Technical Features

• models anisotropic Gaussian processes on 2-dimensional regular grids for a choice of covariance kernels
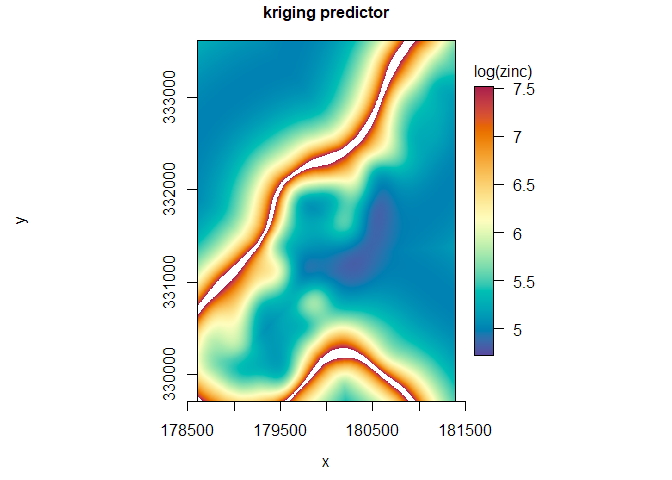
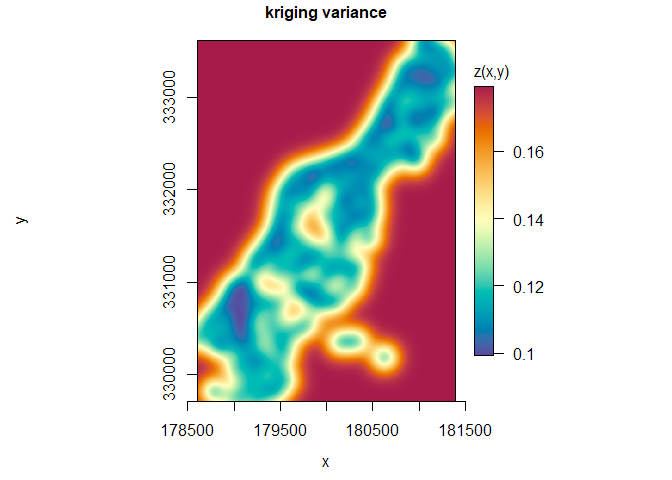
• fast computation of the likelihood function, generalized least squares, and kriging predictor/variance
• Support for missing data problems, and highly optimized code for complete data case
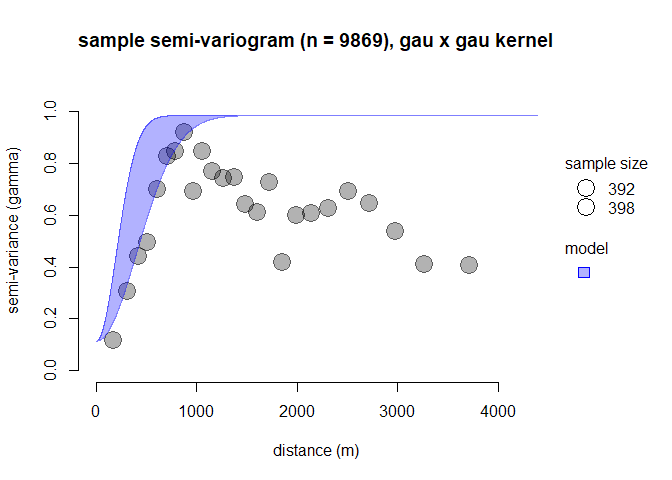
• automated maximum likelihood model fitting with sample semi-variogram diagnostic
• user friendly helper functions for raster down-scaling and point interpolation

Technical Background

This is an R implementation of some methods I developed in my thesis for speeding up geostatistical computations involving large covariance matrices. The central idea is to model spatial dependence using a separable 2-dimensional covariance kernel, defined as the product of two (1-dimensional) univariate covariance kernels. This introduces special symmetries and structure in the covariance matrix, which are exploited in this package for fast and memory-efficient computations.

This package will accompany a paper on fast and efficient downscaling of weather grids so the focus is on a particular application of kriging, but the underlying methods are applicable much more generally. See [1], where I use product kernels to study directions of anisotropy in a nonstationary random fields, and [2, 3], where I apply it to fit acovariance structure, and to speed up calculations of dispersal kernel convolutions.

deankoch/pkern documentation built on Oct. 26, 2023, 8:54 p.m.