README.md

In dominicmagirr/gsdelayed: Design a group-sequential trial when anticipating a delayed effect.

gsdelayed

The goal of gsdelayed is to help with designing a randomized controlled trial, where the endpoint is time-to-event, and a delayed treatment effect is anticipated. Modestly-weighted log-rank statistics are used, which includes the standard log-rank statistic as a special case. Single-stage, two-stage and three-stage designs are accommodated, where the default is to use a Lan-DeMets O’Brien-Fleming alpha-spending function. But the user is free to specify any alpha-spending function they wish. Operating characteristics are calculated via numerical integration (for speed). However simulation functions are also provided that can be used to double-check the chosen design.

Installation

You can install the development version from GitHub with:

# install.packages("devtools")
devtools::install_github("dominicmagirr/gsdelayed")
library(gsdelayed)

Example

Suppose we are designing a RCT where we expect a delayed treatment effect on survival. For example, our alternative hypothesis might look like this:

t_seq <- seq(0,36, length.out = 100)
s_c <- purrr::map_dbl(t_seq, surv_pieces_simple, change_points = c(6), lambdas = log(2) / c(9, 9))
s_e <- purrr::map_dbl(t_seq, surv_pieces_simple, change_points = c(6), lambdas = log(2) / c(9, 16))

plot(t_seq, s_c, ylim = c(0,1), type = "l", 
     xlab = "time (months)", ylab = "survival",
     main = "Alternative hypothesis in an immuno-oncology RCT")
points(t_seq, s_e, lty = 2, type = "l")
legend("topright", c("experimental", "control"), lty = 2:1)

Suppose we are able to recruit 225 patients to each arm (with a uniform recruitment rate) over a 12 month period, and we intend to analyse the data after 30 months from the start of the trial. What is the power, assuming we use a standard log-rank test?

model <- list(change_points = c(6),
             lambdas_0 = c(log(2) / 9, log(2) / 9),
             lambdas_1 = c(log(2) / 9, log(2) / 16))

recruitment <- list(n_0 = 225, n_1 = 225, r_period = 12, k = 1)


## Standard log-rank test (t* = 0)
single_stage_design(t_star = 0,
                    model = model,
                    recruitment = recruitment,
                    dco_final = 30,
                    alpha_one_sided = 0.025)[c("overall_power", "n_events")]
#> $overall_power
#> [1] 0.7978047
#> 
#> $n_events
#> [1] 347.5672

Answer: about 80%. And we expect to observe around 350 events. Given that we anticipate a delayed effect, we can increase power by using a modestly-weighted log-rank test. If we choose the parameter 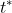equal to 12, we are effectively doing an average landmark analysis from time 12 months until the end of the study (as is discussed here).

# Modestly-weighted log-rank test (t* = 12)
single_stage_design(t_star = 12,
                    model = model,
                    recruitment = recruitment,
                    dco_final = 30,
                    alpha_one_sided = 0.025)[c("overall_power", "n_events")]
#> $overall_power
#> [1] 0.9155788
#> 
#> $n_events
#> [1] 347.5672

2-stage designs

Now suppose we want to add an interim analysis after 18 months. We need to choose how much alpha to spend at the interim. By default the package uses a Lan-DeMets O’Brien-Fleming spending function, and that is what we’ll use in this example. Firstly, for the standard log-rank test…

## Standard log-rank test (t* = 0)
two_stage_design(t_star = 0,
                 model = model,
                 recruitment = recruitment,
                 dco_int = 18,
                 dco_final = 30,
                 alpha_spend_f = ldobf,
                 alpha_one_sided = 0.025)[c("critical_values",
                                            "p_early_stop",
                                            "overall_power",
                                            "expected_t")]
#> $critical_values
#> [1] -2.416430 -2.002319
#> 
#> $p_early_stop
#> under_alternative under_null_approx 
#>       0.172645039       0.007836775 
#> 
#> $overall_power
#> [1] 0.785722
#> 
#> $expected_t
#> under_alternative under_null_approx 
#>          27.92826          29.90596

…and then for the modestly-weighted test (t*=12)…

# Modestly-weighted log-rank test (t* = 12)
two_stage_design(t_star = 12,
                 model = model,
                 recruitment = recruitment,
                 dco_int = 18,
                 dco_final = 30,
                 alpha_spend_f = ldobf,
                 alpha_one_sided = 0.025)[c("critical_values",
                                            "p_early_stop",
                                            "overall_power",
                                            "expected_t")]
#> $critical_values
#> [1] -2.851657 -1.972153
#> 
#> $p_early_stop
#> under_alternative under_null_approx 
#>       0.164187496       0.002174603 
#> 
#> $overall_power
#> [1] 0.9137339
#> 
#> $expected_t
#> under_alternative under_null_approx 
#>          28.02975          29.97390

3-stage designs

We can also extend to three stages. For example, adding another interim analysis at month 24. Firstly, for the standard log-rank test…

## Standard log-rank test (t* = 0)
three_stage_design(t_star = 0,
                   model = model,
                   recruitment = recruitment,
                   dco_int_1 = 18,
                   dco_int_2 = 24,
                   dco_final = 30,
                   alpha_spend_f = ldobf,
                   alpha_one_sided = 0.025)[c("critical_values",
                                              "p_first_int_stop",
                                              "p_second_int_stop",
                                              "overall_power",
                                              "expected_t")]
#> $critical_values
#> [1] -2.416430 -2.178552 -2.058785
#> 
#> $p_first_int_stop
#> under_alternative under_null_approx 
#>       0.172645039       0.007836775 
#> 
#> $p_second_int_stop
#> under_alternative under_null_approx 
#>       0.376275120       0.009155558 
#> 
#> $overall_power
#> [1] 0.7709122
#> 
#> $expected_t
#> under_alternative under_null_approx 
#>          25.67061          29.85103

…and then for the modestly-weighted test (t*=12)…

# Modestly-weighted log-rank test (t* = 12)
three_stage_design(t_star = 12,
                   model = model,
                   recruitment = recruitment,
                   dco_int_1 = 18,
                   dco_int_2 = 24,
                   dco_final = 30,
                   alpha_spend_f = ldobf,
                   alpha_one_sided = 0.025)[c("critical_values",
                                              "p_first_int_stop",
                                              "p_second_int_stop",
                                              "overall_power",
                                              "expected_t")]
#> $critical_values
#> [1] -2.851657 -2.267360 -2.031482
#> 
#> $p_first_int_stop
#> under_alternative under_null_approx 
#>       0.164187496       0.002174603 
#> 
#> $p_second_int_stop
#> under_alternative under_null_approx 
#>        0.54233564        0.01019864 
#> 
#> $overall_power
#> [1] 0.9063206
#> 
#> $expected_t
#> under_alternative under_null_approx 
#>          24.77574          29.91271

dominicmagirr/gsdelayed documentation built on May 15, 2024, 8:24 a.m.