README.md
In dsenturk/mhpca: Multilevel Hybrid Principal Components Analysis
mhpca
The mhpca package is a tool for conducting Multilevel Hybrid Principal
Component Analysis (M-HPCA) proposed in Campos et al. (2021). This
package contains the functions necessary to estimate the marginal
eigenfunctions, eigenvectors, and product eigen components as well as
the tools for performing inference.
Installation
You can install the development version from
GitHub with:
# install.packages("devtools")
devtools::install_github("emjcampos/mhpca")
Example
Begin by loading the mhpca package.
library(mhpca)
Data can be simulated following the low noise, dense simulation set-up
with 15 subjects per group from the supplementary materials using the
following function:
sim = MHPCA_simulation(
sig_eps = 0.25, # measurement error standard deviation
n_d = 15, # number of subjects per group
J = 2, # number of repetitions per subject
D = 2, # number of groups
num_reg = 9, # number of regions
num_time = 50, # number of functional time points
missing_level = FALSE, # whether or not the data should be dense or sparse
K = 2, # number of between-subject marginal regional eigenvectors
L = 2, # number of between-subject marginal functional eigenfunctions
P = 2, # number of within-subject marginal regional eigenvectors
M = 2 # number of within-subject marginal functional eigenfunctions
)
The data must be in the following form, with columns labeled
Repetition, Group, Subject, reg, func, and y.
head(sim$data)
#> Repetition Group Subject reg func y
#> 1 Repetition 1 Group 1 Subject 01 E01 0.00000000 1.1112244
#> 2 Repetition 1 Group 1 Subject 01 E01 0.02040816 1.4425836
#> 3 Repetition 1 Group 1 Subject 01 E01 0.04081633 0.7398267
#> 4 Repetition 1 Group 1 Subject 01 E01 0.06122449 1.4110934
#> 5 Repetition 1 Group 1 Subject 01 E01 0.08163265 1.0086881
#> 6 Repetition 1 Group 1 Subject 01 E01 0.10204082 0.8625667
Using the MHPCA_decomp function, you can estimate the model
components.
MHPCA = MHPCA_decomp(
data = sim$data, # data frame in long format
fve_cutoff = 0.8, # FVE cut-off for reducing the # of product eigen components
nknots = 5, # number of knots for smoothing splines
maxiter = 1000, # maximum iterations for MM algorithm
epsilon = 1e-3, # epsilon value for determining convergence
reduce = TRUE, # reduce the # of product eigen components and re-estimate model
quiet = FALSE # display messages for timing
)
#> 0. Data formatting: 0.016 sec elapsed
#> 1. Estimation of Fixed Effects: 0.16 sec elapsed
#> 2. Estimation of Covariances
#> a. Raw Covariances: 0.191 sec elapsed
#> b,c. Estimation of Marginal Covariances and Smoothing: 0.783 sec elapsed
#> 3. Estimation of Marginal Eigencomponents: 0.004 sec elapsed
#> 4. Estimation of Variance Components
#> a. Fit big model: 4.423 sec elapsed
#> b. Choose number of components: 0.039 sec elapsed
#> c. Final Model: 5.471 sec elapsed
#> d. Prediction: 0.196 sec elapsed
#> MHPCA Decomposition and Estimation: 11.284 sec elapsed
The output of the MHPCA_decomp function
| name | description |
|-------|--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| mu | overall mean function ( vector) |
| eta | group-region-reptition-specific shifts (
vector) |
| eta | group-region-reptition-specific shifts ( data frame with columns for
data frame with columns for Group, reg, Repetition, func, eta) |
| covar | list with the total, between- and within-subject covariances |
| marg | list with the between- and within-subject marginal covariances, eigenvectors, and eigenfunctions |
| model | list with the full and reduced models and their components (scores and variance components) |
| data | data used in the mixed effects model |
| FVE | fraction of variance explained by each product eigen component, G’ and H’ |
Plotting
All of the components can then be plotted and inspected.
Overall Mean Function
The estimated overall mean function
 can be accessed using
can be accessed using MHPCA$mu
ggplot(data.frame(func = unique(sim$data$func), mu = MHPCA$mu)) +
geom_line(aes(x = func, y = mu)) +
labs(
x = TeX("$t$"),
y = TeX("$\\mu(t)$"),
linetype = element_blank()
)

Group-Region-Repetition-Specific Shifts
The estimated group-region-repetition-specific shifts
 can be accessed using
can be accessed using MHPCA$eta
ggplot(MHPCA$eta) +
geom_line(aes(
x = func, y = eta,
color = Group,
linetype = Repetition,
group = interaction(Group, Repetition, reg)
)) +
labs(
y = TeX("$\\eta_{dj}(r, t)$"),
x = TeX("$t$"),
linetype = element_blank(),
color = element_blank()
)

Level 1 Marginal Eigenvectors
The level 1 marginal regional eigenvectors
 for Group 1 are stored in
for Group 1 are stored in
MHPCA$marg$between$regional$'Group 1'$eigendecomp$vectors.
cowplot::plot_grid(
data.frame(MHPCA$marg$between$regional$`Group 1`$eigendecomp$vectors[, 1:2]) %>%
setNames(c("k = 1", "k = 2")) %>%
mutate(reg = unique(sim$data$reg)) %>%
pivot_longer(`k = 1`:`k = 2`, names_to = "k") %>%
ggplot() +
geom_tile(aes(x = reg, fill = value, y = k)) +
scale_fill_distiller(palette = "RdBu") +
labs(
x = "Region, r",
y = element_blank(),
fill = TeX("$v^{(1)}_{1k}(r)$"),
title = "Group 1, Level 1 Eigenvectors"
),
data.frame(MHPCA$marg$between$regional$`Group 2`$eigendecomp$vectors[, 1:2]) %>%
setNames(c("k = 1", "k = 2")) %>%
mutate(reg = unique(sim$data$reg)) %>%
pivot_longer(`k = 1`:`k = 2`, names_to = "k") %>%
ggplot() +
geom_tile(aes(x = reg, fill = value, y = k)) +
scale_fill_distiller(palette = "RdBu") +
labs(
x = "Region, r",
y = element_blank(),
fill = TeX("$v^{(1)}_{2k}(r)$"),
title = "Group 2, Level 1 Eigenvectors"
),
ncol = 2,
labels = c("(a)", "(b)"),
hjust = 0.01,
align = "hv",
axis = "btlr"
)

Level 2 Marignal Eigenvectors
The level 2 marginal regional eigenvectors
 for Group 1 are stored in
for Group 1 are stored in
MHPCA$marg$within$regional$'Group 1'$eigendecomp$vectors.
cowplot::plot_grid(
data.frame(MHPCA$marg$within$regional$`Group 1`$eigendecomp$vectors[, 1:2]) %>%
setNames(c("p = 1", "p = 2")) %>%
mutate(reg = unique(sim$data$reg)) %>%
pivot_longer(`p = 1`:`p = 2`, names_to = "p") %>%
ggplot() +
geom_tile(aes(x = reg, fill = value, y = p)) +
scale_fill_distiller(palette = "RdBu") +
labs(
x = "Region, r",
y = element_blank(),
fill = TeX("$v^{(2)}_{1p}(r)$"),
title = "Group 1, Level 2 Eigenvectors"
),
data.frame(MHPCA$marg$within$regional$`Group 2`$eigendecomp$vectors[, 1:2]) %>%
setNames(c("p = 1", "p = 2")) %>%
mutate(reg = unique(sim$data$reg)) %>%
pivot_longer(`p = 1`:`p = 2`, names_to = "p") %>%
ggplot() +
geom_tile(aes(x = reg, fill = value, y = p)) +
scale_fill_distiller(palette = "RdBu") +
labs(
x = "Region, r",
y = element_blank(),
fill = TeX("$v^{(2)}_{2p}(r)$"),
title = "Group 2, Level 2 Eigenvectors"
),
ncol = 2,
labels = c("(a)", "(b)"),
hjust = 0.01,
align = "hv",
axis = "btlr"
)

Level 1 Marginal Eigenfunctions
The level 1 marginal functional eigenfunctions
 for Group 1 are stored in
for Group 1 are stored in
MHPCA$marg$between$functional$'Group 1'$eigendecomp$vectors.
cowplot::plot_grid(
data.frame(MHPCA$marg$between$functional$`Group 1`$eigendecomp$vectors[, 1:2]) %>%
setNames(c("l = 1", "l = 2")) %>%
mutate(func = unique(sim$data$func)) %>%
pivot_longer(`l = 1`:`l = 2`, names_to = "phi") %>%
ggplot() +
geom_line(aes(x = func, y = value, color = phi)) +
scale_color_brewer(palette = "Dark2") +
labs(
x = "Time, t",
y = TeX("$\\phi_{1l}^{(1)}(t)$"),
color = element_blank(),
title = "Group 1, Level 1 Eigenfunctions"
),
data.frame(MHPCA$marg$between$functional$`Group 2`$eigendecomp$vectors[, 1:2]) %>%
setNames(c("l = 1", "l = 2")) %>%
mutate(func = unique(sim$data$func)) %>%
pivot_longer(`l = 1`:`l = 2`, names_to = "phi") %>%
ggplot() +
geom_line(aes(x = func, y = value, color = phi)) +
scale_color_brewer(palette = "Dark2") +
labs(
x = "Time, t",
y = TeX("$\\phi_{2l}^{(1)}(t)$"),
color = element_blank(),
title = "Group 2, Level 1 Eigenfunctions"
),
ncol = 2,
labels = c("(a)", "(b)"),
hjust = 0.01,
align = "hv",
axis = "btlr"
)

Level 2 Marignal Eigenfunctions
The level 2 marginal functional eigenfunctions
 for Group 1 are stored in
for Group 1 are stored in
MHPCA$marg$within$functional$'Group 1'$eigendecomp$vectors.
cowplot::plot_grid(
data.frame(MHPCA$marg$within$functional$`Group 1`$eigendecomp$vectors[, 1:2]) %>%
setNames(c("m = 1", "m = 2")) %>%
mutate(func = unique(sim$data$func)) %>%
pivot_longer(`m = 1`:`m = 2`, names_to = "phi") %>%
ggplot() +
geom_line(aes(x = func, y = value, color = phi)) +
scale_color_brewer(palette = "Dark2") +
labs(
x = "Time, t",
y = TeX("$\\phi_{1m}^{(2)}(t)$"),
color = TeX("$m$"),
title = "Group 1, Level 2 Eigenfunctions"
),
data.frame(MHPCA$marg$within$functional$`Group 2`$eigendecomp$vectors[, 1:2]) %>%
setNames(c("m = 1", "m = 2")) %>%
mutate(func = unique(sim$data$func)) %>%
pivot_longer(`m = 1`:`m = 2`, names_to = "phi") %>%
ggplot() +
geom_line(aes(x = func, y = value, color = phi)) +
scale_color_brewer(palette = "Dark2") +
labs(
x = "Time, t",
y = TeX("$\\phi_{2m}^{(2)}(t)$"),
color = TeX("$m$"),
title = "Group 2, Level 2 Eigenfunctions"
),
ncol = 2,
labels = c("(a)", "(b)"),
hjust = 0.01,
align = "hv",
axis = "btlr"
)

Summary Tables
Using simulated data, we can calculate the errors of each model
component and display the median, 10th percentile and 90th percentile in
a table, similar to the tables provided in the paper.
groups = unique(data$Group)
names(groups) = groups
parameter_order = c(
"mu", "eta", "y",
"First Level 1 Eigenfunction", "Second Level 1 Eigenfunction",
"First Level 2 Eigenfunction", "Second Level 2 Eigenfunction",
"First Level 1 Eigenvector", "Second Level 1 Eigenvector",
"First Level 2 Eigenvector", "Second Level 2 Eigenvector",
"Level 1", "Level 2", "sigma2", "rho"
)
rbind(
# mu
data.frame(
func = unique(sim$data$func),
estimated = MHPCA$mu,
true = sim$mu
) %>%
summarize(
rse = pracma::trapz(func, (estimated - true) ^ 2) /
pracma::trapz(true ^ 2)
) %>%
mutate(parameter = "mu", .before = 1),
# eta
full_join(
MHPCA$eta %>%
rename(estimated = eta),
map_dfr(sim$eta, function(d) {
map_dfr(d, function(j) {
map_dfr(j, function(r) {
data.frame(true = r) %>%
mutate(func = unique(sim$data$func), .before = 1)
}, .id = "reg")
}, .id = "Repetition")
}, .id = "Group") %>%
mutate(
Repetition = paste("Repetition", Repetition),
reg = paste0("E0", reg),
Group = paste("Group", Group)
),
.by = c("Group", "reg", "Repetition", "func")
) %>%
group_by(Group, Repetition, reg) %>%
summarize(
rse_num = pracma::trapz(func, (estimated - true) ^ 2),
rse_den = pracma::trapz(true ^ 2),
.groups = "drop_last"
) %>%
summarize(
rse = sum(rse_num) / sum(rse_den),
.groups = "drop"
) %>%
mutate(
parameter = "eta",
.before = 1
) %>%
select(parameter, rse),
# level 1 eigenvectors
map_dfr(groups, function(d) {
v_k <- map_dfc(sim$v_k, identity) %>% setNames(c("X1", "X2"))
v_k_hat <- data.frame(
MHPCA$marg$between$regional[[d]]$eigendecomp$vectors
) %>%
dplyr::select(1:ncol(v_k)) %>%
data.frame()
map2_dfc(
v_k, v_k_hat,
~ if(sum((.y - .x)^2) > sum((-.y - .x)^2)) {
-.y
} else {
.y
}
) %>%
mutate(reg = unique(data$reg)) %>%
pivot_longer(X1:X2, names_to = "v", values_to = "estimated") %>%
left_join(
v_k %>%
mutate(reg = unique(data$reg)) %>%
pivot_longer(X1:X2, names_to = "v", values_to = "truth"),
by = c("reg", "v")
) %>%
mutate(
v = case_when(
v == "X1" ~ "First Level 1 Eigenvector",
v == "X2" ~ "Second Level 1 Eigenvector"
)
)
}, .id = "Group") %>%
group_by(Group, v) %>%
summarize(
rse = sum((estimated - truth) ^ 2) / sum(truth ^ 2),
.groups = "drop"
) %>%
mutate(
parameter = v,
.before = 1
) %>%
select(parameter, rse),
# level 2 eigenvectors
map_dfr(groups, function(d) {
v_p <- map_dfc(sim$v_p, identity) %>% setNames(c("X1", "X2"))
v_p_hat <- data.frame(
MHPCA$marg$within$regional[[d]]$eigendecomp$vectors
) %>%
dplyr::select(1:ncol(v_p)) %>%
data.frame()
map2_dfc(
v_p, v_p_hat,
~ if(sum((.y - .x)^2) > sum((-.y - .x)^2)) {
-.y
} else {
.y
}
) %>%
mutate(reg = unique(data$reg)) %>%
pivot_longer(X1:X2, names_to = "v", values_to = "estimated") %>%
left_join(
v_p %>%
mutate(reg = unique(data$reg)) %>%
pivot_longer(X1:X2, names_to = "v", values_to = "truth"),
by = c("reg", "v")
) %>%
mutate(
v = case_when(
v == "X1" ~ "First Level 2 Eigenvector",
v == "X2" ~ "Second Level 2 Eigenvector"
)
)
}, .id = "Group") %>%
group_by(Group, v) %>%
summarize(
rse = sum((estimated - truth) ^ 2) / sum(truth ^ 2),
.groups = "drop"
) %>%
mutate(
parameter = v,
.before = 1
) %>%
select(parameter, rse),
# level 1 eigenfunctions
map_dfr(groups, function(d) {
phi_l <- map_dfc(sim$phi_l, identity) %>% setNames(c("X1", "X2"))
phi_l_hat <- data.frame(
MHPCA$marg$between$functional[[d]]$eigendecomp$vectors
) %>%
dplyr::select(1:ncol(phi_l)) %>%
data.frame()
phi_l_hat <- map2_dfc(
phi_l, phi_l_hat,
~ if(pracma::trapz(unique(data$func), (.y - .x)^2) >
pracma::trapz(unique(data$func), (-.y - .x)^2)) {
-.y
} else {
.y
}
) %>%
mutate(func = unique(data$func))
phi_l %>%
cbind(func = unique(data$func)) %>%
gather(phi, value, -func) %>%
right_join(
phi_l_hat %>% gather(phi, value, -func),
by = c("func", "phi")
) %>%
rename(
truth = value.x,
estimated = value.y
) %>%
mutate(
phi = case_when(
phi == "X1" ~ "First Level 1 Eigenfunction",
phi == "X2" ~ "Second Level 1 Eigenfunction"
)
)
}, .id = "Group") %>%
group_by(Group, phi) %>%
summarize(
rse = pracma::trapz(func, (estimated - truth) ^ 2) /
pracma::trapz(truth ^ 2),
.groups = "drop"
) %>%
mutate(
parameter = phi,
.before = 1
) %>%
select(parameter, rse),
# level 2 eigenfunctions
map_dfr(groups, function(d) {
phi_m <- map_dfc(sim$phi_m, identity) %>% setNames(c("X1", "X2"))
phi_m_hat <- data.frame(
MHPCA$marg$within$functional[[d]]$eigendecomp$vectors
) %>%
dplyr::select(1:ncol(phi_m)) %>%
data.frame()
phi_m_hat <- map2_dfc(
phi_m, phi_m_hat,
~ if(pracma::trapz(unique(data$func), (.y - .x)^2) >
pracma::trapz(unique(data$func), (-.y - .x)^2)) {
-.y
} else {
.y
}
) %>%
mutate(func = unique(data$func))
phi_m %>%
cbind(func = unique(data$func)) %>%
gather(phi, value, -func) %>%
right_join(
phi_m_hat %>% gather(phi, value, -func),
by = c("func", "phi")
) %>%
rename(
truth = value.x,
estimated = value.y
) %>%
mutate(
phi = case_when(
phi == "X1" ~ "First Level 2 Eigenfunction",
phi == "X2" ~ "Second Level 2 Eigenfunction"
)
)
}, .id = "Group") %>%
group_by(Group, phi) %>%
summarize(
rse = pracma::trapz(func, (estimated - truth) ^ 2) /
pracma::trapz(truth ^ 2),
.groups = "drop"
) %>%
mutate(
parameter = phi,
.before = 1
) %>%
select(parameter, rse),
# y prediction
map_dfr(groups, function(d) {
MHPCA$data[[d]] %>%
group_by(Repetition, Subject, reg) %>%
summarize(
RSE_num = pracma::trapz(unique(data$func), (predicted - y)^2),
RSE_den = pracma::trapz(unique(data$func), y^2),
.groups = "drop_last"
) %>%
summarize(
rse = sum(RSE_num) / sum(RSE_den),
.groups = "drop"
)
}, .id = "Group") %>%
mutate(parameter = "y", .before = 1) %>%
select(parameter, rse),
# eigenvalues
rbind(
map_dfr(groups, function(d) {
data.frame(
parameter = "Level 1",
component = MHPCA$model$final[[d]]$level1_components,
estimated = Matrix::diag(MHPCA$model$final[[d]]$Lambda1)
)
}, .id = "Group"),
map_dfr(groups, function(d) {
data.frame(
parameter = "Level 2",
component = MHPCA$model$final[[d]]$level2_components,
estimated = Matrix::diag(MHPCA$model$final[[d]]$Lambda2)
)
}, .id = "Group")
) %>%
left_join(
rbind(
simulated$lambda_kl %>%
rename(
regional = k,
functional = l
) %>%
mutate(level = "between"),
simulated$lambda_pm %>%
rename(
regional = p,
functional = m
) %>%
mutate(level = "within")
) %>%
rename(truth = lambda) %>%
mutate(component = paste(level, regional, functional, sep = "_")),
by = "component") %>%
select(parameter, estimated, truth) %>%
group_by(parameter) %>%
summarize(
rse = (estimated - truth) ^ 2 / truth ^ 2
),
# sigma2
map_dfr(groups, function(d) {
MHPCA$model$final[[d]]$sigma2
}, .id = "Group") %>%
gather(Group, estimated) %>%
mutate(truth = 0.25 ^ 2) %>%
summarize(rse = (estimated - truth) ^ 2 / truth ^ 2) %>%
mutate(parameter = "sigma2"),
# rho
functional_ICC(MHPCA) %>%
mutate(
truth = sum(sim$lambda_kl$lambda) / (sum(sim$lambda_kl$lambda) + sum(sim$lambda_pm$lambda))
) %>%
rename(estimated = rho_dW) %>%
summarize(rse = (estimated - truth) ^ 2 / truth ^ 2) %>%
mutate(parameter = "rho")
) %>%
group_by(parameter) %>%
summarize(
n = n(),
RSE = paste0(
format.pval(
quantile(rse, .5, na.rm = TRUE),
eps = 0.001, digits = 1, nsmall = 3
), " (",
format.pval(
quantile(rse, .1, na.rm = TRUE),
eps = 0.001, digits = 1, nsmall = 3
), ", ",
format.pval(
quantile(rse, .9, na.rm = TRUE),
eps = 0.001, digits = 1, nsmall = 3
), ")"
), .groups = "drop"
) %>%
slice(match(parameter_order, parameter)) %>%
mutate(
parameter = c(
"$\\mu(t)$", "$\\eta_{dj}(r, t)$", "$Y_{dij}(r,t)$",
"$\\phi_{d1}^{(1)}(t)$", "$\\phi^{(1)}_{d2}(t)$",
"$\\phi^{(2)}_{d1}(t)$", "$\\phi^{(2)}_{d2}(t)$",
"$\\nu_{d1}^{(1)}(r)$", "$\\nu_{d2}^{(1)}(r)$",
"$\\nu_{d1}^{(2)}(r)$", "$\\nu_{d2}^{(2)}(r)$",
"$\\lambda_{dg}$", "$\\lambda_{dh}$", "$\\sigma^2_d$",
"$\\rho_{dW}$"
),
.before = 1
) %>%
kbl(
caption = "Percentiles 50\\% (10\\%, 90\\%) of the relative squared errors and normalized mean squared errors for model components based on 1 Monte Carlo run from the simulation design at $n_d = 15$ for the low noise, dense simulation.",
format = "markdown"
) %>%
kable_styling()
#> Warning in kable_styling(.): Please specify format in kable. kableExtra can
#> customize either HTML or LaTeX outputs. See https://haozhu233.github.io/
#> kableExtra/ for details.
| parameter | n | RSE |
|:--------------------------------------------------------------------------------------------------------------------------|----:|:---------------------------------|
|  | 1 | <0.001 (<0.001, <0.001) |
|
| 1 | <0.001 (<0.001, <0.001) |
|  | 4 | <0.001 (<0.001, <0.001) |
|
| 4 | <0.001 (<0.001, <0.001) |
|  | 60 | 0.072 (0.032, 0.252) |
|
| 60 | 0.072 (0.032, 0.252) |
|  | 2 | <0.001 (<0.001, <0.001) |
|
| 2 | <0.001 (<0.001, <0.001) |
|  | 2 | 0.002 (<0.001, 0.002) |
|
| 2 | 0.002 (<0.001, 0.002) |
|  | 2 | <0.001 (<0.001, <0.001) |
|
| 2 | <0.001 (<0.001, <0.001) |
|  | 2 | <0.001 (<0.001, <0.001) |
|
| 2 | <0.001 (<0.001, <0.001) |
|  | 2 | 0.058 (0.012, 0.104) |
|
| 2 | 0.058 (0.012, 0.104) |
|  | 2 | 0.065 (0.020, 0.111) |
|
| 2 | 0.065 (0.020, 0.111) |
|  | 2 | 0.066 (0.015, 0.118) |
|
| 2 | 0.066 (0.015, 0.118) |
|  | 2 | 0.067 (0.017, 0.117) |
|
| 2 | 0.067 (0.017, 0.117) |
|  | 4 | 0.563 (0.159, 0.665) |
|
| 4 | 0.563 (0.159, 0.665) |
|  | 6 | 0.015 (0.010, 0.075) |
|
| 6 | 0.015 (0.010, 0.075) |
|  | 2 | 0.402 (0.297, 0.507) |
|
| 2 | 0.402 (0.297, 0.507) |
|  | 2 | 0.028 (0.022, 0.035) |
| 2 | 0.028 (0.022, 0.035) |
Percentiles 50% (10%, 90%) of the relative squared errors and normalized
mean squared errors for model components based on 1 Monte Carlo run from
the simulation design at
 for the low noise, dense simulation.
for the low noise, dense simulation.
Performing Bootstrapped Tests
In order to draw group-level inference via parametric bootstrap, we can
test the null hypothesis
 with the
with the MHPCA_bootstrap_within function, which performs the bootstrap
sampling in parallel. To demonstrate this function under growing degrees
of departure from the null, the data generation model is modified where
 for
for
 and
and
 for
for
 ,
with larger
,
with larger
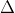 representing larger deviations from the null. Data is generated using
the function
representing larger deviations from the null. Data is generated using
the function MHPCA_simulation_within_group_test
sim = MHPCA_simulation_within_group_test(
sig_eps = 0.25, # measurement error standard deviation
n_d = 15, # number of subjects per group
J = 2, # number of repetitions per subject
D = 2, # number of groups
num_reg = 9, # number of regions
num_time = 50, # number of functional time points
missing_level = FALSE, # whether or not the data should be dense or sparse
test_group = 1, # test group
test_region = 1, # test region
delta = 0.06 # tuning parameter for the degree of departure from null
)
MHPCA = MHPCA_decomp(
data = sim$data, # data frame in long format
fve_cutoff = 0.8, # FVE cut-off for reducing the # of product eigen components
nknots = 5, # number of knots for smoothing splines
maxiter = 1000, # maximum iterations for MM algorithm
epsilon = 1e-3, # epsilon value for determining convergence
reduce = TRUE, # reduce the # of product eigen components and re-estimate model
quiet = FALSE # display messages for timing
)
boot_out = MHPCA_bootstrap_within(
MHPCA = MHPCA,
B = 200, # number of bootstrap samples
region = "E01",
group = "Group 1",
nknots = 5,
quiet = FALSE
)
#> 0. Setup Parametric Bootstrap Components: 0.064 sec elapsed
#> 1. Bootstrap Procedure: 411.859 sec elapsed
#> 2. Calculate p-values: 0.233 sec elapsed
#> Bootstrap Procedure: 412.156 sec elapsed
The output of this function is a list with elements pval (the
bootstrapped p-value for the test) and boots (the estimated
 for each bootstrapped sample).
for each bootstrapped sample).
For tests between groups, we test the null hypothesis
 with the
with the MHPCA_bootstrap_between function, which performs the
bootstrap sampling in parallel.
boot_out = MHPCA_bootstrap_between(
MHPCA = MHPCA,
B = 200, # number of bootstrap samples
region = "E01",
group = c("Group 1", "Group 2"),
nknots = 5,
quiet = FALSE
)
The output of this function is the similar to the output of
MHPCA_bootstrap_within, however boots contains the estimated
 .
.
dsenturk/mhpca documentation built on Dec. 20, 2021, 2:11 a.m.
mhpca
The mhpca package is a tool for conducting Multilevel Hybrid Principal
Component Analysis (M-HPCA) proposed in Campos et al. (2021). This
package contains the functions necessary to estimate the marginal
eigenfunctions, eigenvectors, and product eigen components as well as
the tools for performing inference.
Installation
You can install the development version from GitHub with:
# install.packages("devtools")
devtools::install_github("emjcampos/mhpca")
Example
Begin by loading the mhpca package.
library(mhpca)
Data can be simulated following the low noise, dense simulation set-up with 15 subjects per group from the supplementary materials using the following function:
sim = MHPCA_simulation(
sig_eps = 0.25, # measurement error standard deviation
n_d = 15, # number of subjects per group
J = 2, # number of repetitions per subject
D = 2, # number of groups
num_reg = 9, # number of regions
num_time = 50, # number of functional time points
missing_level = FALSE, # whether or not the data should be dense or sparse
K = 2, # number of between-subject marginal regional eigenvectors
L = 2, # number of between-subject marginal functional eigenfunctions
P = 2, # number of within-subject marginal regional eigenvectors
M = 2 # number of within-subject marginal functional eigenfunctions
)
The data must be in the following form, with columns labeled
Repetition, Group, Subject, reg, func, and y.
head(sim$data)
#> Repetition Group Subject reg func y
#> 1 Repetition 1 Group 1 Subject 01 E01 0.00000000 1.1112244
#> 2 Repetition 1 Group 1 Subject 01 E01 0.02040816 1.4425836
#> 3 Repetition 1 Group 1 Subject 01 E01 0.04081633 0.7398267
#> 4 Repetition 1 Group 1 Subject 01 E01 0.06122449 1.4110934
#> 5 Repetition 1 Group 1 Subject 01 E01 0.08163265 1.0086881
#> 6 Repetition 1 Group 1 Subject 01 E01 0.10204082 0.8625667
Using the MHPCA_decomp function, you can estimate the model
components.
MHPCA = MHPCA_decomp(
data = sim$data, # data frame in long format
fve_cutoff = 0.8, # FVE cut-off for reducing the # of product eigen components
nknots = 5, # number of knots for smoothing splines
maxiter = 1000, # maximum iterations for MM algorithm
epsilon = 1e-3, # epsilon value for determining convergence
reduce = TRUE, # reduce the # of product eigen components and re-estimate model
quiet = FALSE # display messages for timing
)
#> 0. Data formatting: 0.016 sec elapsed
#> 1. Estimation of Fixed Effects: 0.16 sec elapsed
#> 2. Estimation of Covariances
#> a. Raw Covariances: 0.191 sec elapsed
#> b,c. Estimation of Marginal Covariances and Smoothing: 0.783 sec elapsed
#> 3. Estimation of Marginal Eigencomponents: 0.004 sec elapsed
#> 4. Estimation of Variance Components
#> a. Fit big model: 4.423 sec elapsed
#> b. Choose number of components: 0.039 sec elapsed
#> c. Final Model: 5.471 sec elapsed
#> d. Prediction: 0.196 sec elapsed
#> MHPCA Decomposition and Estimation: 11.284 sec elapsed
The output of the MHPCA_decomp function
| name | description |
|-------|--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| mu | overall mean function ( vector) |
| eta | group-region-reptition-specific shifts (
data frame with columns for
Group, reg, Repetition, func, eta) |
| covar | list with the total, between- and within-subject covariances |
| marg | list with the between- and within-subject marginal covariances, eigenvectors, and eigenfunctions |
| model | list with the full and reduced models and their components (scores and variance components) |
| data | data used in the mixed effects model |
| FVE | fraction of variance explained by each product eigen component, G’ and H’ |
Plotting
All of the components can then be plotted and inspected.
Overall Mean Function
The estimated overall mean function
can be accessed using
MHPCA$mu
ggplot(data.frame(func = unique(sim$data$func), mu = MHPCA$mu)) +
geom_line(aes(x = func, y = mu)) +
labs(
x = TeX("$t$"),
y = TeX("$\\mu(t)$"),
linetype = element_blank()
)

Group-Region-Repetition-Specific Shifts
The estimated group-region-repetition-specific shifts
can be accessed using
MHPCA$eta
ggplot(MHPCA$eta) +
geom_line(aes(
x = func, y = eta,
color = Group,
linetype = Repetition,
group = interaction(Group, Repetition, reg)
)) +
labs(
y = TeX("$\\eta_{dj}(r, t)$"),
x = TeX("$t$"),
linetype = element_blank(),
color = element_blank()
)

Level 1 Marginal Eigenvectors
The level 1 marginal regional eigenvectors
for Group 1 are stored in
MHPCA$marg$between$regional$'Group 1'$eigendecomp$vectors.
cowplot::plot_grid(
data.frame(MHPCA$marg$between$regional$`Group 1`$eigendecomp$vectors[, 1:2]) %>%
setNames(c("k = 1", "k = 2")) %>%
mutate(reg = unique(sim$data$reg)) %>%
pivot_longer(`k = 1`:`k = 2`, names_to = "k") %>%
ggplot() +
geom_tile(aes(x = reg, fill = value, y = k)) +
scale_fill_distiller(palette = "RdBu") +
labs(
x = "Region, r",
y = element_blank(),
fill = TeX("$v^{(1)}_{1k}(r)$"),
title = "Group 1, Level 1 Eigenvectors"
),
data.frame(MHPCA$marg$between$regional$`Group 2`$eigendecomp$vectors[, 1:2]) %>%
setNames(c("k = 1", "k = 2")) %>%
mutate(reg = unique(sim$data$reg)) %>%
pivot_longer(`k = 1`:`k = 2`, names_to = "k") %>%
ggplot() +
geom_tile(aes(x = reg, fill = value, y = k)) +
scale_fill_distiller(palette = "RdBu") +
labs(
x = "Region, r",
y = element_blank(),
fill = TeX("$v^{(1)}_{2k}(r)$"),
title = "Group 2, Level 1 Eigenvectors"
),
ncol = 2,
labels = c("(a)", "(b)"),
hjust = 0.01,
align = "hv",
axis = "btlr"
)

Level 2 Marignal Eigenvectors
The level 2 marginal regional eigenvectors
for Group 1 are stored in
MHPCA$marg$within$regional$'Group 1'$eigendecomp$vectors.
cowplot::plot_grid(
data.frame(MHPCA$marg$within$regional$`Group 1`$eigendecomp$vectors[, 1:2]) %>%
setNames(c("p = 1", "p = 2")) %>%
mutate(reg = unique(sim$data$reg)) %>%
pivot_longer(`p = 1`:`p = 2`, names_to = "p") %>%
ggplot() +
geom_tile(aes(x = reg, fill = value, y = p)) +
scale_fill_distiller(palette = "RdBu") +
labs(
x = "Region, r",
y = element_blank(),
fill = TeX("$v^{(2)}_{1p}(r)$"),
title = "Group 1, Level 2 Eigenvectors"
),
data.frame(MHPCA$marg$within$regional$`Group 2`$eigendecomp$vectors[, 1:2]) %>%
setNames(c("p = 1", "p = 2")) %>%
mutate(reg = unique(sim$data$reg)) %>%
pivot_longer(`p = 1`:`p = 2`, names_to = "p") %>%
ggplot() +
geom_tile(aes(x = reg, fill = value, y = p)) +
scale_fill_distiller(palette = "RdBu") +
labs(
x = "Region, r",
y = element_blank(),
fill = TeX("$v^{(2)}_{2p}(r)$"),
title = "Group 2, Level 2 Eigenvectors"
),
ncol = 2,
labels = c("(a)", "(b)"),
hjust = 0.01,
align = "hv",
axis = "btlr"
)

Level 1 Marginal Eigenfunctions
The level 1 marginal functional eigenfunctions
for Group 1 are stored in
MHPCA$marg$between$functional$'Group 1'$eigendecomp$vectors.
cowplot::plot_grid(
data.frame(MHPCA$marg$between$functional$`Group 1`$eigendecomp$vectors[, 1:2]) %>%
setNames(c("l = 1", "l = 2")) %>%
mutate(func = unique(sim$data$func)) %>%
pivot_longer(`l = 1`:`l = 2`, names_to = "phi") %>%
ggplot() +
geom_line(aes(x = func, y = value, color = phi)) +
scale_color_brewer(palette = "Dark2") +
labs(
x = "Time, t",
y = TeX("$\\phi_{1l}^{(1)}(t)$"),
color = element_blank(),
title = "Group 1, Level 1 Eigenfunctions"
),
data.frame(MHPCA$marg$between$functional$`Group 2`$eigendecomp$vectors[, 1:2]) %>%
setNames(c("l = 1", "l = 2")) %>%
mutate(func = unique(sim$data$func)) %>%
pivot_longer(`l = 1`:`l = 2`, names_to = "phi") %>%
ggplot() +
geom_line(aes(x = func, y = value, color = phi)) +
scale_color_brewer(palette = "Dark2") +
labs(
x = "Time, t",
y = TeX("$\\phi_{2l}^{(1)}(t)$"),
color = element_blank(),
title = "Group 2, Level 1 Eigenfunctions"
),
ncol = 2,
labels = c("(a)", "(b)"),
hjust = 0.01,
align = "hv",
axis = "btlr"
)

Level 2 Marignal Eigenfunctions
The level 2 marginal functional eigenfunctions
for Group 1 are stored in
MHPCA$marg$within$functional$'Group 1'$eigendecomp$vectors.
cowplot::plot_grid(
data.frame(MHPCA$marg$within$functional$`Group 1`$eigendecomp$vectors[, 1:2]) %>%
setNames(c("m = 1", "m = 2")) %>%
mutate(func = unique(sim$data$func)) %>%
pivot_longer(`m = 1`:`m = 2`, names_to = "phi") %>%
ggplot() +
geom_line(aes(x = func, y = value, color = phi)) +
scale_color_brewer(palette = "Dark2") +
labs(
x = "Time, t",
y = TeX("$\\phi_{1m}^{(2)}(t)$"),
color = TeX("$m$"),
title = "Group 1, Level 2 Eigenfunctions"
),
data.frame(MHPCA$marg$within$functional$`Group 2`$eigendecomp$vectors[, 1:2]) %>%
setNames(c("m = 1", "m = 2")) %>%
mutate(func = unique(sim$data$func)) %>%
pivot_longer(`m = 1`:`m = 2`, names_to = "phi") %>%
ggplot() +
geom_line(aes(x = func, y = value, color = phi)) +
scale_color_brewer(palette = "Dark2") +
labs(
x = "Time, t",
y = TeX("$\\phi_{2m}^{(2)}(t)$"),
color = TeX("$m$"),
title = "Group 2, Level 2 Eigenfunctions"
),
ncol = 2,
labels = c("(a)", "(b)"),
hjust = 0.01,
align = "hv",
axis = "btlr"
)

Summary Tables
Using simulated data, we can calculate the errors of each model component and display the median, 10th percentile and 90th percentile in a table, similar to the tables provided in the paper.
groups = unique(data$Group)
names(groups) = groups
parameter_order = c(
"mu", "eta", "y",
"First Level 1 Eigenfunction", "Second Level 1 Eigenfunction",
"First Level 2 Eigenfunction", "Second Level 2 Eigenfunction",
"First Level 1 Eigenvector", "Second Level 1 Eigenvector",
"First Level 2 Eigenvector", "Second Level 2 Eigenvector",
"Level 1", "Level 2", "sigma2", "rho"
)
rbind(
# mu
data.frame(
func = unique(sim$data$func),
estimated = MHPCA$mu,
true = sim$mu
) %>%
summarize(
rse = pracma::trapz(func, (estimated - true) ^ 2) /
pracma::trapz(true ^ 2)
) %>%
mutate(parameter = "mu", .before = 1),
# eta
full_join(
MHPCA$eta %>%
rename(estimated = eta),
map_dfr(sim$eta, function(d) {
map_dfr(d, function(j) {
map_dfr(j, function(r) {
data.frame(true = r) %>%
mutate(func = unique(sim$data$func), .before = 1)
}, .id = "reg")
}, .id = "Repetition")
}, .id = "Group") %>%
mutate(
Repetition = paste("Repetition", Repetition),
reg = paste0("E0", reg),
Group = paste("Group", Group)
),
.by = c("Group", "reg", "Repetition", "func")
) %>%
group_by(Group, Repetition, reg) %>%
summarize(
rse_num = pracma::trapz(func, (estimated - true) ^ 2),
rse_den = pracma::trapz(true ^ 2),
.groups = "drop_last"
) %>%
summarize(
rse = sum(rse_num) / sum(rse_den),
.groups = "drop"
) %>%
mutate(
parameter = "eta",
.before = 1
) %>%
select(parameter, rse),
# level 1 eigenvectors
map_dfr(groups, function(d) {
v_k <- map_dfc(sim$v_k, identity) %>% setNames(c("X1", "X2"))
v_k_hat <- data.frame(
MHPCA$marg$between$regional[[d]]$eigendecomp$vectors
) %>%
dplyr::select(1:ncol(v_k)) %>%
data.frame()
map2_dfc(
v_k, v_k_hat,
~ if(sum((.y - .x)^2) > sum((-.y - .x)^2)) {
-.y
} else {
.y
}
) %>%
mutate(reg = unique(data$reg)) %>%
pivot_longer(X1:X2, names_to = "v", values_to = "estimated") %>%
left_join(
v_k %>%
mutate(reg = unique(data$reg)) %>%
pivot_longer(X1:X2, names_to = "v", values_to = "truth"),
by = c("reg", "v")
) %>%
mutate(
v = case_when(
v == "X1" ~ "First Level 1 Eigenvector",
v == "X2" ~ "Second Level 1 Eigenvector"
)
)
}, .id = "Group") %>%
group_by(Group, v) %>%
summarize(
rse = sum((estimated - truth) ^ 2) / sum(truth ^ 2),
.groups = "drop"
) %>%
mutate(
parameter = v,
.before = 1
) %>%
select(parameter, rse),
# level 2 eigenvectors
map_dfr(groups, function(d) {
v_p <- map_dfc(sim$v_p, identity) %>% setNames(c("X1", "X2"))
v_p_hat <- data.frame(
MHPCA$marg$within$regional[[d]]$eigendecomp$vectors
) %>%
dplyr::select(1:ncol(v_p)) %>%
data.frame()
map2_dfc(
v_p, v_p_hat,
~ if(sum((.y - .x)^2) > sum((-.y - .x)^2)) {
-.y
} else {
.y
}
) %>%
mutate(reg = unique(data$reg)) %>%
pivot_longer(X1:X2, names_to = "v", values_to = "estimated") %>%
left_join(
v_p %>%
mutate(reg = unique(data$reg)) %>%
pivot_longer(X1:X2, names_to = "v", values_to = "truth"),
by = c("reg", "v")
) %>%
mutate(
v = case_when(
v == "X1" ~ "First Level 2 Eigenvector",
v == "X2" ~ "Second Level 2 Eigenvector"
)
)
}, .id = "Group") %>%
group_by(Group, v) %>%
summarize(
rse = sum((estimated - truth) ^ 2) / sum(truth ^ 2),
.groups = "drop"
) %>%
mutate(
parameter = v,
.before = 1
) %>%
select(parameter, rse),
# level 1 eigenfunctions
map_dfr(groups, function(d) {
phi_l <- map_dfc(sim$phi_l, identity) %>% setNames(c("X1", "X2"))
phi_l_hat <- data.frame(
MHPCA$marg$between$functional[[d]]$eigendecomp$vectors
) %>%
dplyr::select(1:ncol(phi_l)) %>%
data.frame()
phi_l_hat <- map2_dfc(
phi_l, phi_l_hat,
~ if(pracma::trapz(unique(data$func), (.y - .x)^2) >
pracma::trapz(unique(data$func), (-.y - .x)^2)) {
-.y
} else {
.y
}
) %>%
mutate(func = unique(data$func))
phi_l %>%
cbind(func = unique(data$func)) %>%
gather(phi, value, -func) %>%
right_join(
phi_l_hat %>% gather(phi, value, -func),
by = c("func", "phi")
) %>%
rename(
truth = value.x,
estimated = value.y
) %>%
mutate(
phi = case_when(
phi == "X1" ~ "First Level 1 Eigenfunction",
phi == "X2" ~ "Second Level 1 Eigenfunction"
)
)
}, .id = "Group") %>%
group_by(Group, phi) %>%
summarize(
rse = pracma::trapz(func, (estimated - truth) ^ 2) /
pracma::trapz(truth ^ 2),
.groups = "drop"
) %>%
mutate(
parameter = phi,
.before = 1
) %>%
select(parameter, rse),
# level 2 eigenfunctions
map_dfr(groups, function(d) {
phi_m <- map_dfc(sim$phi_m, identity) %>% setNames(c("X1", "X2"))
phi_m_hat <- data.frame(
MHPCA$marg$within$functional[[d]]$eigendecomp$vectors
) %>%
dplyr::select(1:ncol(phi_m)) %>%
data.frame()
phi_m_hat <- map2_dfc(
phi_m, phi_m_hat,
~ if(pracma::trapz(unique(data$func), (.y - .x)^2) >
pracma::trapz(unique(data$func), (-.y - .x)^2)) {
-.y
} else {
.y
}
) %>%
mutate(func = unique(data$func))
phi_m %>%
cbind(func = unique(data$func)) %>%
gather(phi, value, -func) %>%
right_join(
phi_m_hat %>% gather(phi, value, -func),
by = c("func", "phi")
) %>%
rename(
truth = value.x,
estimated = value.y
) %>%
mutate(
phi = case_when(
phi == "X1" ~ "First Level 2 Eigenfunction",
phi == "X2" ~ "Second Level 2 Eigenfunction"
)
)
}, .id = "Group") %>%
group_by(Group, phi) %>%
summarize(
rse = pracma::trapz(func, (estimated - truth) ^ 2) /
pracma::trapz(truth ^ 2),
.groups = "drop"
) %>%
mutate(
parameter = phi,
.before = 1
) %>%
select(parameter, rse),
# y prediction
map_dfr(groups, function(d) {
MHPCA$data[[d]] %>%
group_by(Repetition, Subject, reg) %>%
summarize(
RSE_num = pracma::trapz(unique(data$func), (predicted - y)^2),
RSE_den = pracma::trapz(unique(data$func), y^2),
.groups = "drop_last"
) %>%
summarize(
rse = sum(RSE_num) / sum(RSE_den),
.groups = "drop"
)
}, .id = "Group") %>%
mutate(parameter = "y", .before = 1) %>%
select(parameter, rse),
# eigenvalues
rbind(
map_dfr(groups, function(d) {
data.frame(
parameter = "Level 1",
component = MHPCA$model$final[[d]]$level1_components,
estimated = Matrix::diag(MHPCA$model$final[[d]]$Lambda1)
)
}, .id = "Group"),
map_dfr(groups, function(d) {
data.frame(
parameter = "Level 2",
component = MHPCA$model$final[[d]]$level2_components,
estimated = Matrix::diag(MHPCA$model$final[[d]]$Lambda2)
)
}, .id = "Group")
) %>%
left_join(
rbind(
simulated$lambda_kl %>%
rename(
regional = k,
functional = l
) %>%
mutate(level = "between"),
simulated$lambda_pm %>%
rename(
regional = p,
functional = m
) %>%
mutate(level = "within")
) %>%
rename(truth = lambda) %>%
mutate(component = paste(level, regional, functional, sep = "_")),
by = "component") %>%
select(parameter, estimated, truth) %>%
group_by(parameter) %>%
summarize(
rse = (estimated - truth) ^ 2 / truth ^ 2
),
# sigma2
map_dfr(groups, function(d) {
MHPCA$model$final[[d]]$sigma2
}, .id = "Group") %>%
gather(Group, estimated) %>%
mutate(truth = 0.25 ^ 2) %>%
summarize(rse = (estimated - truth) ^ 2 / truth ^ 2) %>%
mutate(parameter = "sigma2"),
# rho
functional_ICC(MHPCA) %>%
mutate(
truth = sum(sim$lambda_kl$lambda) / (sum(sim$lambda_kl$lambda) + sum(sim$lambda_pm$lambda))
) %>%
rename(estimated = rho_dW) %>%
summarize(rse = (estimated - truth) ^ 2 / truth ^ 2) %>%
mutate(parameter = "rho")
) %>%
group_by(parameter) %>%
summarize(
n = n(),
RSE = paste0(
format.pval(
quantile(rse, .5, na.rm = TRUE),
eps = 0.001, digits = 1, nsmall = 3
), " (",
format.pval(
quantile(rse, .1, na.rm = TRUE),
eps = 0.001, digits = 1, nsmall = 3
), ", ",
format.pval(
quantile(rse, .9, na.rm = TRUE),
eps = 0.001, digits = 1, nsmall = 3
), ")"
), .groups = "drop"
) %>%
slice(match(parameter_order, parameter)) %>%
mutate(
parameter = c(
"$\\mu(t)$", "$\\eta_{dj}(r, t)$", "$Y_{dij}(r,t)$",
"$\\phi_{d1}^{(1)}(t)$", "$\\phi^{(1)}_{d2}(t)$",
"$\\phi^{(2)}_{d1}(t)$", "$\\phi^{(2)}_{d2}(t)$",
"$\\nu_{d1}^{(1)}(r)$", "$\\nu_{d2}^{(1)}(r)$",
"$\\nu_{d1}^{(2)}(r)$", "$\\nu_{d2}^{(2)}(r)$",
"$\\lambda_{dg}$", "$\\lambda_{dh}$", "$\\sigma^2_d$",
"$\\rho_{dW}$"
),
.before = 1
) %>%
kbl(
caption = "Percentiles 50\\% (10\\%, 90\\%) of the relative squared errors and normalized mean squared errors for model components based on 1 Monte Carlo run from the simulation design at $n_d = 15$ for the low noise, dense simulation.",
format = "markdown"
) %>%
kable_styling()
#> Warning in kable_styling(.): Please specify format in kable. kableExtra can
#> customize either HTML or LaTeX outputs. See https://haozhu233.github.io/
#> kableExtra/ for details.
| parameter | n | RSE |
|:--------------------------------------------------------------------------------------------------------------------------|----:|:---------------------------------|
| | 1 | <0.001 (<0.001, <0.001) |
|
| 4 | <0.001 (<0.001, <0.001) |
|
| 60 | 0.072 (0.032, 0.252) |
|
| 2 | <0.001 (<0.001, <0.001) |
|
| 2 | 0.002 (<0.001, 0.002) |
|
| 2 | <0.001 (<0.001, <0.001) |
|
| 2 | <0.001 (<0.001, <0.001) |
|
| 2 | 0.058 (0.012, 0.104) |
|
| 2 | 0.065 (0.020, 0.111) |
|
| 2 | 0.066 (0.015, 0.118) |
|
| 2 | 0.067 (0.017, 0.117) |
|
| 4 | 0.563 (0.159, 0.665) |
|
| 6 | 0.015 (0.010, 0.075) |
|
| 2 | 0.402 (0.297, 0.507) |
|
| 2 | 0.028 (0.022, 0.035) |
Percentiles 50% (10%, 90%) of the relative squared errors and normalized
mean squared errors for model components based on 1 Monte Carlo run from
the simulation design at
for the low noise, dense simulation.
Performing Bootstrapped Tests
In order to draw group-level inference via parametric bootstrap, we can
test the null hypothesis
with the
MHPCA_bootstrap_within function, which performs the bootstrap
sampling in parallel. To demonstrate this function under growing degrees
of departure from the null, the data generation model is modified where
for
and
for
,
with larger
representing larger deviations from the null. Data is generated using
the function
MHPCA_simulation_within_group_test
sim = MHPCA_simulation_within_group_test(
sig_eps = 0.25, # measurement error standard deviation
n_d = 15, # number of subjects per group
J = 2, # number of repetitions per subject
D = 2, # number of groups
num_reg = 9, # number of regions
num_time = 50, # number of functional time points
missing_level = FALSE, # whether or not the data should be dense or sparse
test_group = 1, # test group
test_region = 1, # test region
delta = 0.06 # tuning parameter for the degree of departure from null
)
MHPCA = MHPCA_decomp(
data = sim$data, # data frame in long format
fve_cutoff = 0.8, # FVE cut-off for reducing the # of product eigen components
nknots = 5, # number of knots for smoothing splines
maxiter = 1000, # maximum iterations for MM algorithm
epsilon = 1e-3, # epsilon value for determining convergence
reduce = TRUE, # reduce the # of product eigen components and re-estimate model
quiet = FALSE # display messages for timing
)
boot_out = MHPCA_bootstrap_within(
MHPCA = MHPCA,
B = 200, # number of bootstrap samples
region = "E01",
group = "Group 1",
nknots = 5,
quiet = FALSE
)
#> 0. Setup Parametric Bootstrap Components: 0.064 sec elapsed
#> 1. Bootstrap Procedure: 411.859 sec elapsed
#> 2. Calculate p-values: 0.233 sec elapsed
#> Bootstrap Procedure: 412.156 sec elapsed
The output of this function is a list with elements pval (the
bootstrapped p-value for the test) and boots (the estimated
for each bootstrapped sample).
For tests between groups, we test the null hypothesis
with the
MHPCA_bootstrap_between function, which performs the
bootstrap sampling in parallel.
boot_out = MHPCA_bootstrap_between(
MHPCA = MHPCA,
B = 200, # number of bootstrap samples
region = "E01",
group = c("Group 1", "Group 2"),
nknots = 5,
quiet = FALSE
)
The output of this function is the similar to the output of
MHPCA_bootstrap_within, however boots contains the estimated
.
Add the following code to your website.
For more information on customizing the embed code, read Embedding Snippets.
