README.md
In jasondubois/spopmodel: Methods for and Application of Fish Population Dynamics Model
spopmodel
This R package contains algorithms (i.e., functions & methods) and some
data to explore (i.e., model) population dynamics of some fish species.
Specifically, this model was designed for San Francisco Estuary-based
(SFE) White Sturgeon (Acipenser transmontanus) but could be applied to
SFE-based Striped Bass (Morone saxatilis) or other species where
pertinent data (see section \<>) are known or available. (The s in
spopmodel implies sturgeon or striped bass and is a nod to
model developer Shannon B.)
Overview
The collaborative effort between the California Department of Fish and
Wildlife (CDFW) and the University of Idaho (College of Natural
Resources; UICNR) gave rise to spopmodel. CDFW supplied data and UICNR
produced model formulae and R-script. spopmodel facilitates the
deployment, application, sharing, and understanding of this population
dynamics model.
The model’s primary application will guide management of the SFE-based
White Sturgeon fishery. This stochastic age-based model yields
population growth rate
(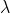 )
over varying exploitation
(
)
over varying exploitation
(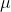 ) per set
period (e.g., 20 years).
) per set
period (e.g., 20 years). spopmodel attempts to make easier the process
of exploring different management scenarios and for viewing — among
other outcomes — the effects of
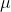 on
on
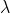 .
.
Though developed using White Sturgeon data, this model (in theory)
should[1] be applicable to other datasets having like inputs (see
section Data Requirements). However, spopmodel does provide users
with functions (or methods) for “every day” analytics (e.g., length-(or
age-)frequency; descriptive statistics; growth model given age & length
data).
Data Requirements
Model inputs need to be age-based. To yield
 , one needs per age: frequency[2]; egg count[3];
spawning probability[4]; and survival probability[5].
, one needs per age: frequency[2]; egg count[3];
spawning probability[4]; and survival probability[5].
This model employs a female-based Leslie Matrix with stochasticity
(given probability values of input data). Other data not directly
inputted to the model are exploitation
(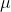 ; from
mark-recapture), length-frequency (adjusted for gear selectivity),
male-to-female ratio, and population estimate for the appropriate
demographic.
; from
mark-recapture), length-frequency (adjusted for gear selectivity),
male-to-female ratio, and population estimate for the appropriate
demographic.
Help documentation is available for the various datasets included
herein. Try ?<dataset name> at the R prompt (>).
Other R Packages
Currently, spopmodel imports msm, popbio, & reshape2. From these
packages, spopmodel uses the functions listed below. Base-R functions
(or methods) are used where needed. Further, spopmodel employs gear
selectivity code developed by R.
Millar, not available in an
R package.
msm::deltamethod()popbio::betaval()popbio::stretchbetaval()popbio::pop.projection()reshape2::dcast()reshape2::melt()
Vignettes
Currently, there are three vignettes available: simulations;
model_inputs; and bcla_growth. Once you’ve installed and then loaded
spopmodel, call each vignette using the code below.
utils::vignette(package = "spopmodel", topic = "<vignette_name>")
Datasets
spopmodel contains six datasets available for use. Each dataset has a
help file, as viewed by either help("<dataset_name>") or
?<dataset_name>. To view each dataset, simply type the dataset name at
the command prompt (>) or call View(<dataset_name>).
| Dataset Name | Useage |
| --------------- | ----------------------------- |
| age_dist | model input |
| number_eggs | model input |
| prob_spawn | model input |
| prob_survival | model input |
| trammel_catch | growth rate, gear selectivity |
| fin_ray_aging | back-calculated length-at-age |
Examples
Herein, we provide some examples for running the model using “built-in”
datasets. Please also see vignettes by typing vignette(package =
"spopmodel").
Start by loading spopmodel in your current R session. If you have
not done so, install this package from GitHub using the code below.
# ********** not run - run only if needed, need to run only once *****
# if (!(require(devtools))) install.packages(pkgs = "devtools")
# devtools::install_github(repo = "jasondubois/spopmodel")
# ********************************************************************
# load library to current session
library(spopmodel)
Growth Rate
Here we demonstrate how to estimate growth rate using von Bertalanffy
Growth Model. We need to create some length bins, so let’s see our
length range using range(trammel_catch[["FL"]]). We see fork length
ranges from 53 to 217, so bins from 50 to 220 by 5 cm will work just
fine.
len_breaks <- seq(from = 50, to = 220, by = 5)
Now let’s age the non-aged portion of our trammel net sample. We do this
using AgeEach(), which will assign ages to each fish without an age.
See ?AgeEach for help file.
Displaying “BinDiagnostics” shows BinCheck (empty length bins [no
ages] or where all ages present could not be assigned an age),
CountNA (number of ages as NA; i.e., could not be aged), and
CountTotal (total sample size).
ages <- AgeEach(
data = trammel_catch,
len = FL,
age = Age,
lenBreaks = len_breaks
)
ages[["BinDiagnostics"]]
#> $BinCheck
#> [185,190) [190,195) [195,200) [205,210) [210,215) [215,220)
#> "empty" "all NA" "empty" "empty" "empty" "all NA"
#>
#> $CountNA
#> [1] 2
#>
#> $CountTotal
#> [1] 1000
To run the von Bertalanffy Growth Model (using FitVBGM()), we’ll need
to assign the AgeEach() output to a field in trammel_catch. We’ll
call this new field AgeAll to maintain (i.e., not overwrite) the Age
field. Note: upon running code below, trammel_net will now be in
your Global environment with the added field. To see the original (if
necessary), run spopmodel::trammel_catch.
trammel_catch$AgeAll <- ages[["Ages"]]
Here we use FitVBGM() to fit the von Bertalanffy Growth Model.
FitVBGM() uses stats::nls() and as such requires some starting
values. Pass starting values as a list with Linf (asymptotic length),
K (growth rate), and t0 (supposed age at zero size). In
start_vals, we’ve chosen these values somewhat arbitrarily but are
based some on Kohlhorst et
al. 1980.
Though we don’t show it here, we could use fit to predict length given
age, and then plot predicted values over age \~ length. Note: model
fit fails with singular gradient or other errors. I am looking into
the problem. For now, below provide an example using data and
FitVBGM().
start_vals <- list(Linf = 500, K = 0.3, t0 = -3.638)
fit <- FitVBGM(
data = trammel_catch,
len = FL,
age = AgeAll,
start = start_vals,
control = list(warnOnly = TRUE, maxiter = 1000)
)
summary(fit)
#>
#> Formula: FL ~ Linf * (1 - exp(-K * (AgeAll - t0)))
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> Linf -115.89571 33.46528 -3.463 0.000557 ***
#> K -0.03400 0.00502 -6.772 2.16e-11 ***
#> t0 -9.20656 1.22591 -7.510 1.31e-13 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 9.145 on 995 degrees of freedom
#>
#> Number of iterations to convergence: 10
#> Achieved convergence tolerance: 5.492e-06
#> (2 observations deleted due to missingness)
-
emphasized as to date (2019-05-02) model not run on other data
-
where frequency is proportion
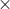 population estimate
population estimate
-
along with some measure of error (standard deviation)
-
along with some measure of error (standard deviation)
-
along with some measure of error (standard deviation)
jasondubois/spopmodel documentation built on Dec. 4, 2019, 9:12 p.m.
spopmodel
This R package contains algorithms (i.e., functions & methods) and some
data to explore (i.e., model) population dynamics of some fish species.
Specifically, this model was designed for San Francisco Estuary-based
(SFE) White Sturgeon (Acipenser transmontanus) but could be applied to
SFE-based Striped Bass (Morone saxatilis) or other species where
pertinent data (see section \<>) are known or available. (The s in
spopmodel implies sturgeon or striped bass and is a nod to
model developer Shannon B.)
Overview
The collaborative effort between the California Department of Fish and
Wildlife (CDFW) and the University of Idaho (College of Natural
Resources; UICNR) gave rise to spopmodel. CDFW supplied data and UICNR
produced model formulae and R-script. spopmodel facilitates the
deployment, application, sharing, and understanding of this population
dynamics model.
The model’s primary application will guide management of the SFE-based
White Sturgeon fishery. This stochastic age-based model yields
population growth rate
()
over varying exploitation
(
) per set
period (e.g., 20 years).
spopmodel attempts to make easier the process
of exploring different management scenarios and for viewing — among
other outcomes — the effects of
on
.
Though developed using White Sturgeon data, this model (in theory)
should[1] be applicable to other datasets having like inputs (see
section Data Requirements). However, spopmodel does provide users
with functions (or methods) for “every day” analytics (e.g., length-(or
age-)frequency; descriptive statistics; growth model given age & length
data).
Data Requirements
Model inputs need to be age-based. To yield
, one needs per age: frequency[2]; egg count[3];
spawning probability[4]; and survival probability[5].
This model employs a female-based Leslie Matrix with stochasticity
(given probability values of input data). Other data not directly
inputted to the model are exploitation
(; from
mark-recapture), length-frequency (adjusted for gear selectivity),
male-to-female ratio, and population estimate for the appropriate
demographic.
Help documentation is available for the various datasets included
herein. Try ?<dataset name> at the R prompt (>).
Other R Packages
Currently, spopmodel imports msm, popbio, & reshape2. From these
packages, spopmodel uses the functions listed below. Base-R functions
(or methods) are used where needed. Further, spopmodel employs gear
selectivity code developed by R.
Millar, not available in an
R package.
msm::deltamethod()popbio::betaval()popbio::stretchbetaval()popbio::pop.projection()reshape2::dcast()reshape2::melt()
Vignettes
Currently, there are three vignettes available: simulations;
model_inputs; and bcla_growth. Once you’ve installed and then loaded
spopmodel, call each vignette using the code below.
utils::vignette(package = "spopmodel", topic = "<vignette_name>")
Datasets
spopmodel contains six datasets available for use. Each dataset has a
help file, as viewed by either help("<dataset_name>") or
?<dataset_name>. To view each dataset, simply type the dataset name at
the command prompt (>) or call View(<dataset_name>).
| Dataset Name | Useage |
| --------------- | ----------------------------- |
| age_dist | model input |
| number_eggs | model input |
| prob_spawn | model input |
| prob_survival | model input |
| trammel_catch | growth rate, gear selectivity |
| fin_ray_aging | back-calculated length-at-age |
Examples
Herein, we provide some examples for running the model using “built-in”
datasets. Please also see vignettes by typing vignette(package =
"spopmodel").
Start by loading spopmodel in your current R session. If you have
not done so, install this package from GitHub using the code below.
# ********** not run - run only if needed, need to run only once *****
# if (!(require(devtools))) install.packages(pkgs = "devtools")
# devtools::install_github(repo = "jasondubois/spopmodel")
# ********************************************************************
# load library to current session
library(spopmodel)
Growth Rate
Here we demonstrate how to estimate growth rate using von Bertalanffy
Growth Model. We need to create some length bins, so let’s see our
length range using range(trammel_catch[["FL"]]). We see fork length
ranges from 53 to 217, so bins from 50 to 220 by 5 cm will work just
fine.
len_breaks <- seq(from = 50, to = 220, by = 5)
Now let’s age the non-aged portion of our trammel net sample. We do this
using AgeEach(), which will assign ages to each fish without an age.
See ?AgeEach for help file.
Displaying “BinDiagnostics” shows BinCheck (empty length bins [no
ages] or where all ages present could not be assigned an age),
CountNA (number of ages as NA; i.e., could not be aged), and
CountTotal (total sample size).
ages <- AgeEach(
data = trammel_catch,
len = FL,
age = Age,
lenBreaks = len_breaks
)
ages[["BinDiagnostics"]]
#> $BinCheck
#> [185,190) [190,195) [195,200) [205,210) [210,215) [215,220)
#> "empty" "all NA" "empty" "empty" "empty" "all NA"
#>
#> $CountNA
#> [1] 2
#>
#> $CountTotal
#> [1] 1000
To run the von Bertalanffy Growth Model (using FitVBGM()), we’ll need
to assign the AgeEach() output to a field in trammel_catch. We’ll
call this new field AgeAll to maintain (i.e., not overwrite) the Age
field. Note: upon running code below, trammel_net will now be in
your Global environment with the added field. To see the original (if
necessary), run spopmodel::trammel_catch.
trammel_catch$AgeAll <- ages[["Ages"]]
Here we use FitVBGM() to fit the von Bertalanffy Growth Model.
FitVBGM() uses stats::nls() and as such requires some starting
values. Pass starting values as a list with Linf (asymptotic length),
K (growth rate), and t0 (supposed age at zero size). In
start_vals, we’ve chosen these values somewhat arbitrarily but are
based some on Kohlhorst et
al. 1980.
Though we don’t show it here, we could use fit to predict length given
age, and then plot predicted values over age \~ length. Note: model
fit fails with singular gradient or other errors. I am looking into
the problem. For now, below provide an example using data and
FitVBGM().
start_vals <- list(Linf = 500, K = 0.3, t0 = -3.638)
fit <- FitVBGM(
data = trammel_catch,
len = FL,
age = AgeAll,
start = start_vals,
control = list(warnOnly = TRUE, maxiter = 1000)
)
summary(fit)
#>
#> Formula: FL ~ Linf * (1 - exp(-K * (AgeAll - t0)))
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> Linf -115.89571 33.46528 -3.463 0.000557 ***
#> K -0.03400 0.00502 -6.772 2.16e-11 ***
#> t0 -9.20656 1.22591 -7.510 1.31e-13 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 9.145 on 995 degrees of freedom
#>
#> Number of iterations to convergence: 10
#> Achieved convergence tolerance: 5.492e-06
#> (2 observations deleted due to missingness)
-
emphasized as to date (2019-05-02) model not run on other data
-
where frequency is proportion
population estimate
-
along with some measure of error (standard deviation)
-
along with some measure of error (standard deviation)
-
along with some measure of error (standard deviation)
Add the following code to your website.
For more information on customizing the embed code, read Embedding Snippets.
