README.md
In jpmeagher/vbar: Variational Bayes Ancestral Reconstruction

vbar

The goal of vbar is to implement Variational Bayes Ancestral Reconstruction for collections of discrete and continuous phenotypic traits given a phylogeny of evolutionary relationships between species. Discrete traits may be ordinal or nominal, while continuous traits may be scalar- or function-valued. Ancestral Reconstruction is based on the Phylogenetic Latent Variable Model (PLVM) for trait evolution. This model accommodates repeated measurements for extant species.

This readme is laid out as follows: after presenting code installing the vbar package, the Generalised Phylogenetic Latent Variable Model (PLVM) for trait evolution is outlined. In order to illustrate more clearly the assumptions underpinning this model, a synthetic data set is generated from the PLVM. Approximate Bayesian Inference for this synthetic data set, which is included with the package, demonstrates how the vbar package is applied for Ancestral Reconstruction.

For the code required to fit the generalised PLVM to data, skip to the section on Approximate Bayesian Inference

You can install the development version from GitHub with:

# install.packages("devtools")
devtools::install_github("jpmeagher/vbar")

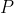Consider the $D$ -dimensional observation of $P$ discrete- or continuous-valued manifest traits $\boldsymbol y_{sn} = \left( y_{sn 1}, \dots, y_{snD} \right)^\top$ , specific to individual $n = 1, \dots, N_s$ within taxon $s = 1, \dots, S$ , where traits may be ordinal-, nominal-, scalar- or function-valued.

The shared evolutionary history between taxa is modeled as a known, fixed phylogeny $\mathcal T = \left\{ \mathcal V, \mathcal B \right\}$ . $\mathcal T$ is a bifurcating, directed, acyclic graph tree with nodes $\mathcal V = \left\{ v_1, \dots, v_{2S - 1} \right\}$ linked by branches $\mathcal B = \left\{ b_1, \dots, b_{2S - 2} \right\}$ . The graph originates at the degree-2 root node $v_{2S - 1}$ and terminates at the degree-1 terminal nodes $v_1. \dots, v_{S}$ corresponding to the extant taxa. Node $v_s$ is linked to its parent $v_{\operatorname{pa} \left( s \right)}$ by the branch of length $b_s$ for all $s = 1, \dots, 2S - 2$ . For notational convenience, we let $\boldsymbol t \in \mathcal T$ denote a continuous position along a branch of $\mathcal T$ , where $\boldsymbol t_s$ denotes the position of node $v_s$ for all $s = 1, \dots, 2S - 1$ . Furthermore, the patristic distance operator $d_{\mathcal T} \left( \boldsymbol t, \boldsymbol t' \right)$ defines the shortest path from $\boldsymbol t$ to $\boldsymbol t'$ over $\mathcal T$ .

For each manifest trait, we introduce auxiliary traits $\boldsymbol x_{sn} = \left( x_{s n 1}, \dots, x_{sn D'} \right)^\top \in \mathbb R^{D'}$ such that $D' \geq D$ , there exists a deterministic map $g : \boldsymbol x_{sn} \to \boldsymbol y_{sn}$ , and auxiliary traits mapping $y_{snd}$ are indexed by $d'$ . This allows us to adopt a probit model for discrete traits.

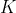If $y_{snd} = k$ for $k = 1, \dots, K$ is a nominal trait belonging to one of $K$ unordered categories, we have a 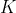$K$ -to-1 mapping such that

$y_{snd} = g \left( x_{s, n, d'} , \dots, x_{s, n,d' + K - 1} \right) = c_{k}, \text{ if } x_{s, n, d' + k - 1} = \max \left\{ x_{s, n, d'} , \dots, x_{s, n, d' + K - 1} \right\}.$

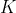If $y_{id'} = k$ for $k = 1, \dots, K$ is an ordinal trait belonging to one of $K$ ordered categories, we have a 1-to-1 mapping

$y_{snd} = g \left( x_{snd} \right) = k, \text{if } \gamma_{k-1} \leq x_{snd} \< \gamma_{k},$

given thresholds $\boldsymbol \gamma = \left( \gamma_{0}, \gamma_{1} \dots, \gamma_{K} \right)^\top$ where $\gamma_{k - 1} \< \gamma_k$ , $\gamma_0 = -\infty$ , $\gamma_1 = 0$ , and $\gamma_K = \infty$ . Finally, if $y_{snd}$ takes continuous values, then any bijective map to the real numbers is appropriate. We then assume that

$\boldsymbol x_{sn} \sim \mathcal N \left( \boldsymbol \mu_{sn}, \Lambda^{-1}\right),$

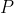where $\boldsymbol \mu_{sn} = \left( \mu_{sn1}, \dots, \mu_{snD'}^s \right)^\top \in \mathbb R^{D'}$ is the expected auxiliary trait and $\Lambda$ is a diagonal precision matrix parameterised by $\boldsymbol \lambda = \left( \lambda_1, \dots, \lambda_{P} \right) \in \mathbb R_+^{P}$ . Note that we consider one independent precision parameter for each of the $P$ manifest traits, where $\Lambda_{d'd'} = \lambda_p$ when $x_{snd'}$ maps to the $p^{th}$ manifest trait and $\lambda_p = 1$ is fixed when that trait is discrete.

In order to define the PLVM, let

$\boldsymbol \mu_{sn} = \boldsymbol W \boldsymbol z_{sn}$

where $\boldsymbol W \in \mathbb R^{D' \times L}$ is the loading matrix with columns denoted $\boldsymbol w_l$ for $l = 1, \dots, L$ , rows $\boldsymbol w_{d'}$ for $d' = 1, \dots, D'$ , and $\boldsymbol z_{sn} = \left( z_{sn1}, \dots, z_{snL} \right)^\top \in \mathbb R^{L}$ is the individual-specific latent trait. We link $\boldsymbol z_{sn}$ to the taxon-specific latent trait $\boldsymbol f_s = \left( f_{s1}, \dots, f_{sL} \right)^\top \in \mathbb R^{L}$ by setting

$z_{snl} = \sqrt{1 - \tau_l^2}f_{sl} + \tau_l \, \epsilon_{snl},$

where $\tau_l \in \left( 0, 1 \right)$ is the standard deviation of the inter-taxon variation driven by $\epsilon_{snl} \sim \mathcal N \left(0, 1 \right)$ and we have $\boldsymbol \tau = \left( \tau_1, \dots, \tau_L \right)^\top$ . Taxon-specific latent traits are modelled as independent phylogenetic Ornstein-Uhlenbeck (OP) processes over $\mathcal T$ such that

$\begin{aligned} f_{sl} &= f_l \left( \boldsymbol t_s \right), \\ f_l \left( \boldsymbol t \right) &\sim \mathcal{GP} \left( 0, k_l \left( \boldsymbol t, \boldsymbol t' \right) \right), \\ k_l \left( \boldsymbol t, \boldsymbol t' \right) &= h_l^2 \exp \left( - \frac{d_{\mathcal T} \left( \boldsymbol t, \boldsymbol t' \right) }{\ell} \right) + \left( 1 - h_l^2\right) \delta_{\boldsymbol t} \, \delta_{\boldsymbol t'} \end{aligned}$

where $h_l^2 \in \left( 0, 1 \right)$ is the heritability of the $l^{th}$ latent trait such that $\boldsymbol h = \left(h_1, \dots, h_L\right)^\top$ , $\ell = 2$ is the fixed phylogenetic length-scale, and

$\delta_{\mathcal t} = \begin{cases} 1, & \text{if }\boldsymbol t \in \left\{ \boldsymbol t_1, \dots, \boldsymbol t_S\right\}, \\ 0, & \text{otherwise,} \end{cases}$

identifies extant taxa. Restricting $h_l$ and $\ell$ in this manner avoids scale invariance in the Gaussian likelihood, but still provides a flexible model for latent trait evolution, similar to the Phylogenetic Mixed Model for trait evolution.

The OU process is a Gauss-Markov process. As such, it can be shown that

$\begin{aligned} f_{2S - 1, l} &\sim \mathcal N \left( 0, h_l^2 \right)\\ f_{sl} \mid f_{\operatorname{pa} \left( s \right),l} &\sim \mathcal N \left( \nu_{s, l} f_{\operatorname{pa} \left( s \right),l}, \eta_{s, l}^2 \right) \end{aligned}$

where, setting $k_{s,s', l} = k_l \left( \boldsymbol t_s, \boldsymbol t_{s'} \right)$ and $k_{s, l} = k_l \left( \boldsymbol t_s, \boldsymbol t_{s} \right)$ ,

$\begin{aligned} \nu_{sl} &= k_{s, \operatorname{pa} \left( s \right),l} k_{\operatorname{pa} \left( s \right), l}^{-1}, \\ &= \exp\left( -\frac{d_{\mathcal T} \left( \boldsymbol t_s, \boldsymbol t_{\operatorname{pa} \left( s \right)} \right) }{\ell}\right), \\ \eta_{sl}^2 &= k_{s, l} - \nu_{s, l} \, k_{\operatorname{pa} \left( s \right), s, l}, \\ &= h_l^2 \left( 1 - \exp \left( - 2 \frac{d_{\mathcal T} \left( \boldsymbol t_s, \boldsymbol t_{\operatorname{pa} \left( s \right)} \right) }{\ell} \right) \right) + \left( 1 - h_l^2\right) \delta_{\boldsymbol t_s} \end{aligned}$

for $s = 1, \dots 2S - 1$ . We also define $\boldsymbol \nu_s = \left(\nu_{s1}, \dots, \nu_{sL} \right)^\top$ and $\boldsymbol \eta_s = \left(\eta_{s1}, \dots, \eta_{sL} \right)^\top$ at this point.

The PLVM admits conjugate priors for the loading $\boldsymbol W$ and free auxiliary trait precision parameters $\boldsymbol \lambda$ when we have

$\begin{aligned} \boldsymbol w_l \mid \alpha_l &\sim \mathcal N \left( \boldsymbol 0, \alpha_l^{-1} \boldsymbol C_w \right), \\ \lambda_p &\sim \begin{cases} \delta \left( 1 \right), & \text{if } p \text{ is a discrete trait}, \\ \operatorname{Gamma} \left( a_\lambda, b_\lambda \right), &\text{otherwise}, \end{cases} \end{aligned}$

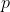where $\alpha_l \in \mathbb R_+$ is the Automatic Relevance Determination (ARD) precision hyperparameter such that $\boldsymbol \alpha = \left( \alpha_1, \dots, \alpha_L \right)^\top$ , $\boldsymbol C_w$ is a fixed covariance matrix enforcing smoothness constraints on $\boldsymbol w_q$ , and $a_\lambda$ and $b_\lambda$ are shape and rate hyperparameters for precision associated with trait $p$ taking values along a continuum, and we let $\delta \left( 1 \right)$ denote the one-point distribution with all its mass at $1$ .

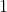The PLVM also provides a direct approach to approach to ancestral reconstruction. Firstly, note that this model for trait evolution allows for within-taxon variation on the latent traits, governed by $\boldsymbol \tau$ . Stripping away this stochastic effect on trait evolution allows us define taxon-specific manifest and auxiliary traits, $\boldsymbol y_s$ and $\boldsymbol x_s$ , such that

$\boldsymbol x_s \sim \mathcal N \left( \boldsymbol W \left( \boldsymbol I_L - \Sigma_{\tau} \right)^{1/2} \boldsymbol f_s, \Lambda^{-1} \right)$

for $s = 1, \dots, 2S - 1$ , $g : \boldsymbol x_s \to \boldsymbol y_s$ as before, and $\Sigma_{\tau}$ is the diagonal covariance matrix parametrised by $\left( \tau_1^2, \dots, \tau_L^2\right)^\top$ .

Before outlining our approach inference for the PLVM, we sample from the model. This provides the synthetic data set we use to validate the inference scheme. We require the following packages.

library(vbar)
library(ape)
library(ggplot2)
library(magrittr)
library(reshape2)
library(dplyr)
library(mvnfast)
library(HDInterval)
library(ggpubr)

Our analysis considers $S = 128$ extant taxa with a shared evolutionary history defined by the phylogeny below. We label the root node and its children for future reference. Note that the ape package labels the root node $S+1$ by default.

S <- 2^7
set.seed(98)
phy <- rcoal(S) %>% 
  scale_phylo(max_dist = 1)

$P = 4$ traits are recorded for $N_s = 3$ individuals in the extant taxon $s = 1, \dots, S$ . These traits consist of an ordinal trait with $K = 4$ ordered categories, a nominal trait with $K = 3$ unordered categories, a scalar-valued continuous trait, and a strictly positive function-valued trait registered to 32 equidistant points along the unit interval. Thus, $\boldsymbol y_{sn}$ and $\boldsymbol x_{sn}$ are $D = 35$ and $D' = 37$ dimensional vectors respectively.

P <- 4
N_s <- rep(3, S)
N <- sum(N_s)
K_ord <- 4
K_nom <- 3

Auxiliary traits are generated by a PLVM with $L = 3$ latent traits, parameterised by $\boldsymbol W$ and $\boldsymbol \lambda = \left(1, 1, 10, 10000 \right)^\top$ such that auxiliary traits associated with discrete traits have precision 1, the scalar-valued continuous trait has precision 10, and the function-valued trait has precision of 10000. The loading matrix $\boldsymbol W$ is presented below.

auxiliary_trait_precision <- c(1, 1, 10, 10000)
L <- 3 
# FVT Loading
D_fvt <- 2^5 
x_fvt <- seq(0, 1, length.out = D_fvt) 
loading_fvt_means <- c(.2, .5, .75)
loading_fvt_sds <- c(.06, .12, .07)
loading_fvt <- sapply(
  seq_along(loading_fvt_means), 
  function(i) dnorm(x_fvt, mean = loading_fvt_means[i], sd = loading_fvt_sds[i])
  )
loading_fvt <- loading_fvt %*% diag(1 / c(5, 4, 6))
# Continuous Trait Loading
loading_con <- c(0.5, 0.25, -0.25)
# Nominal Trait loading
loading_nom <- matrix(c(1, 0, 0, 0, -0.5, 0, 0, 0, 1), byrow = TRUE, nrow = K_nom, ncol = L)
# Ordinal Trait Loading
loading_ord <- c(0, 1, 0.5)
# Full Loading
loading <- rbind(loading_ord, loading_nom, loading_con, loading_fvt)
rownames(loading) <- c(
  "ord", 
  paste("nom", 1:K_nom, sep = "."),
  "con", 
  paste("fvt", 1:D_fvt, sep = ".")
)
colnames(loading) <- paste("loading", 1:L, sep = ".")

The distribution of taxon- and individual-specific latent traits is defined by the phylogenetic hyperparameters $\boldsymbol \tau = \left( \sqrt{0.001}, \sqrt{0.05}, \sqrt{0.1} \right)^\top$ and $\boldsymbol h = \left( \sqrt{0.95}, \sqrt{0.66}, \sqrt{0.25} \right)^\top$ and so we sample $\boldsymbol z_{sn}$ .

tau <- sqrt(c(0.001, 0.05, 0.1))
h <- sqrt(c(0.95, 0.66, 0.25))

set.seed(99)
taxon_specific_latent_traits <- sapply(
  h, function(x) {
    simulate_phylogenetic_ou(
      phy = phy, 
      heritable_amplitude = x, length_scale = 2,
      environmental_amplitude = sqrt(1 - x^2),
      internal = TRUE
    )
  }
)

taxon_id <- sapply(1:S, function(i) rep(phy$tip.label[i], N_s[i])) %>% 
  c()

individual_specific_latent_traits <- sapply(
  1:L, function(l){
    sqrt(1 - tau[l]^2) * taxon_specific_latent_traits[taxon_id, l] + 
      tau[l] * rnorm(N)
  })

Given $\boldsymbol W$ , $\boldsymbol z_{sn}$ , and $\boldsymbol \lambda$ , we can define $\boldsymbol \mu_{sn}$ and sample $\boldsymbol x_{sn}$ .

D_prime <- nrow(loading)
auxiliary_traits_expectation <- individual_specific_latent_traits %*% t(loading)
auxiliary_trait_precision_vec <- c(
  auxiliary_trait_precision[1], 
  rep(auxiliary_trait_precision[2], K_nom), 
  auxiliary_trait_precision[3], 
  rep(auxiliary_trait_precision[4], D_fvt)
)

set.seed(100)
auxiliary_traits <- auxiliary_traits_expectation + 
  t(
    sapply(1:N, function(i){
      rnorm(D_prime, sd = sqrt(1 / auxiliary_trait_precision_vec))
      }
      )
    )

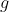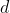We map $\boldsymbol x_{sn}$ to $\boldsymbol y_{sn}$ by $g$ given the ordinal trait cut-off points $\boldsymbol \gamma = \left( -\infty, 0, 0.5, 1, \infty \right)^\top$ . Furthermore, we set $g \left( x_{snd} \right) = \exp \left( x_{snd} \right) = y_{snd}$ when the index $d$ corresponds to a function-valued trait.

cut_off_points <- c(-Inf, 0, 0.5, 1, Inf)

auxiliary_index_ord <- 1
auxiliary_index_nom <- max(auxiliary_index_ord) + (1:K_nom)
auxiliary_index_con <- max(auxiliary_index_nom) + 1
auxiliary_index_fvt <- max(auxiliary_index_con) + 1:D_fvt

manifest_traits <- data.frame(
  taxon_id = taxon_id,
  ord = sapply(auxiliary_traits[, auxiliary_index_ord], function(x){
    x > cut_off_points
  }) %>% 
    colSums() %>% 
    factor(ordered = TRUE),
  nom = apply(auxiliary_traits[, auxiliary_index_nom], 1, which.max) %>% 
    factor(ordered = FALSE),
  con = auxiliary_traits[, auxiliary_index_con],
  fvt = exp(unname(auxiliary_traits[, auxiliary_index_fvt]))
)

Given the mapping 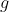$g$ , loading $\boldsymbol W$ , auxiliary trait precision parameters $\boldsymbol \lambda$ , individual-specific latent traits, and phylogenetic hyperparameters $\boldsymbol \tau$ and $\boldsymbol h$ , we can explore the distribution of taxon-specific manifest traits $\boldsymbol y_s$ for any $s = 1, \dots, 2S - 1$ .

covariance_ou <- ou_kernel(
  dist.nodes(phy),
  amplitude = 1, length_scale = 2
)
covariance_f <- lapply(h, function(x){
  tmp <- x^2 * covariance_ou
  tmp[1:S, 1:S] <- tmp[1:S, 1:S] + (1 - x^2)* diag(S)
  colnames(tmp) <- rownames(tmp) <- c(phy$tip.label, S + (1:(S-1)))
  tmp
})
covariance_zf <- lapply(1:L, function(i){
  tmp <- (1 - tau[i]^2) * covariance_f[[i]]
  tmp <- tmp[
    c(taxon_id, phy$tip.label, S + (1:(S-1))), 
    c(taxon_id, phy$tip.label, S + (1:(S-1)))
    ]
  tmp[1:N, 1:N] <- tmp[1:N, 1:N] + tau[i]^2 * diag(N)
  tmp
})

ancestral_mean <- sapply(1:L, function(i){
  (covariance_zf[[i]][-(1:N), (1:N)] %*% 
     chol2inv(chol(covariance_zf[[i]][(1:N), (1:N)])) %*% 
     individual_specific_latent_traits[, i])[, 1]
})
ancestral_cov <- lapply(1:L, function(i){
  covariance_zf[[i]][-(1:N), -(1:N)] - 
    covariance_zf[[i]][-(1:N), (1:N)] %*% 
    chol2inv(chol(covariance_zf[[i]][(1:N), (1:N)])) %*% 
    covariance_zf[[i]][(1:N), -(1:N)]
})
ancestral_sd <- sapply(ancestral_cov, function(X){
  sqrt(diag(X))
})

a <- "130" # ancestor
M <- 1000 # samples for ancestral reconstruction

scaled_taxon_latent_trait_ar <- rmvn(
  M, mu = ancestral_mean[a,], sigma = diag(ancestral_sd[a, ]), isChol = TRUE
  )
auxiliary_trait_ar <- scaled_taxon_latent_trait_ar %*% t(loading) + 
  t(
    sapply(1:M, function(i){
      rnorm(D_prime, sd = sqrt(1 / auxiliary_trait_precision_vec))
      }
      )
    )

manifest_trait_ar <- data.frame(
  ord = sapply(auxiliary_trait_ar[, auxiliary_index_ord], function(x){
    x > cut_off_points
  }) %>% 
    colSums() %>% 
    factor(ordered = TRUE),
  nom = apply(auxiliary_trait_ar[, auxiliary_index_nom], 1, which.max) %>% 
    factor(ordered = FALSE),
  con = auxiliary_trait_ar[, auxiliary_index_con],
  fvt = exp(unname(auxiliary_trait_ar[, auxiliary_index_fvt]))
)

Our objective is to infer a posterior distribution over individual-specific auxiliary traits, the PLVM loading, individual- and taxon-specific latent traits, and free auxiliary trait precision parameters given manifest traits, a fixed phylogeny, and priors on the model parameters. That is

$\begin{aligned} p \left( \boldsymbol X, \boldsymbol W, \boldsymbol Z, \boldsymbol F \mid \boldsymbol Y, \mathcal T, \boldsymbol \psi \right) &\propto p \left(\boldsymbol Y \mid \boldsymbol X, \boldsymbol \gamma \right) p \left( \boldsymbol X \mid \boldsymbol W, \boldsymbol Z, \boldsymbol \lambda \right) p \left( \boldsymbol Z \mid \boldsymbol F, \boldsymbol \tau \right) p \left( \boldsymbol F \mid \boldsymbol h \right) p \left( \boldsymbol W \mid \boldsymbol \alpha \right) p \left( \boldsymbol \lambda \mid a_\lambda, b_\lambda \right), \end{aligned}$

which can be expressed as

$\begin{aligned} p \left( \boldsymbol X, \boldsymbol W, \boldsymbol Z, \boldsymbol F \mid \boldsymbol Y, \mathcal T, \boldsymbol \psi \right) &\propto \left( \prod_{n = 1}^N p \left(\boldsymbol y_n \mid \boldsymbol x_n \right) p \left( \boldsymbol x_n \mid \boldsymbol W, \boldsymbol z_n, \boldsymbol \lambda \right) \right) \left( \prod_{s = 1}^S \prod_{n = 1}^{N_s} p \left( \boldsymbol z_{sn} \mid \boldsymbol f_s, \boldsymbol \tau \right) \right) \\ &\left( \prod_{s = 1}^{2S - 2} p \left( \boldsymbol f_s \mid \boldsymbol f_{\operatorname{pa} \left( s \right)}, \boldsymbol h \right) p \left( \boldsymbol f_{2S - 1} \mid \boldsymbol h \right) \right) \prod_{l = 1}^L p \left( \boldsymbol w_l \mid \alpha_l, \boldsymbol C_w \right) \prod_{p = 1}^{P} p \left( \lambda_p \mid a_\lambda, b_\lambda \right), \end{aligned}$

where we have introduced the notation $\boldsymbol Y = \left( \boldsymbol y_{11}, \dots, \boldsymbol y_{1N_1}, \dots, \boldsymbol y_{S1}, \dots, \boldsymbol y_{SN_S} \right)^\top = \left( \boldsymbol y_1, \dots, \boldsymbol y_N \right)^\top$ for $N = \sum_{s = 1}^S N_s$ which suppresses the index $s$ , $\boldsymbol X$ and $\boldsymbol Z$ have analogous definitions, and $\boldsymbol \psi = \left\{\boldsymbol \gamma, \boldsymbol \tau, \boldsymbol h, \boldsymbol \alpha, \boldsymbol C_w, a_\lambda, b_\lambda \right\}$ model hyperparameters. $\boldsymbol z_{sn}$ and $\boldsymbol z_n$ are used interchangeably as is most convenient. This hierarchical model is defined by the distributions over manifest and auxiliary variables

$\begin{aligned} \boldsymbol y_n \mid \boldsymbol x_n, \boldsymbol \gamma &= g \left( \boldsymbol x_n \right), \\ \boldsymbol x_n \mid \boldsymbol W, \boldsymbol z_n, \boldsymbol \lambda &\sim \mathcal N \left( \boldsymbol W \boldsymbol z_n, \Lambda^{-1}\right), \\ \end{aligned}$

latent variables

$\begin{aligned} \boldsymbol z_{sn} \mid \boldsymbol f_s, \boldsymbol \tau &\sim \mathcal N \left(\left( \boldsymbol I_L - \Sigma_\tau \right)^{1/2} \boldsymbol f_s, \Sigma_\tau\right), \\ \boldsymbol f_s \mid \boldsymbol f_{\operatorname{pa} \left( s \right)}, \boldsymbol h &\sim \mathcal N \left( \operatorname{diag} \left( \boldsymbol \nu_s\right) \boldsymbol f_{\operatorname{pa} \left( s \right)}, \Sigma_{\eta, s} \right), \\ \boldsymbol f_{2S - 1} \mid \boldsymbol h &\sim \mathcal N \left( \boldsymbol 0, \Sigma_h \right), \end{aligned}$

and parameters

$\begin{aligned} \boldsymbol w_q \mid \boldsymbol \alpha, \boldsymbol C_w &\sim \mathcal N \left( \boldsymbol 0, \alpha_l^{-1} \boldsymbol C_w \right), \\ \lambda_p &\sim \begin{cases} \delta \left( 1 \right), & \text{if } p \text{ is a discrete trait}, \\ \operatorname{Gamma} \left( a_\lambda, b_\lambda \right), &\text{otherwise}, \end{cases} \end{aligned}$

where $\Sigma_{\tau}$ is the diagonal covariance matrix parametrised by $\left( \tau_1^2, \dots, \tau_L^2\right)^\top$ , $\Sigma_{\eta, }$ is the diagonal covariance matrix parametrised by $\left( \tau_1^2, \dots, \tau_L^2\right)^\top$ .

A Co-ordinate Ascent Variational Inference (CAVI) algorithm allows approximate Bayesian Inference for this model. To implement this inference scheme we use the vbar package.

We start by decluttering the global environment.

rm(list = ls())

The synthetic data set of manifest traits for $N = 384$ individuals across $S = 128$ extant taxa is included with the vbar package. It consists of 5 variables. That is an id variable taxon_id alongside 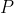$P$ traits, namely the ordinal trait ord, the nominal trait nom, the continuous trait con, and the function-valued trait fvt. Note that the fvt variable is a list of lists, such that each element consists of a numeric vector of length 32.

synthetic_traits %>% str(list.len = 5) 
#> 'data.frame':    384 obs. of  5 variables:
#>  $ taxon_id: chr  "t18" "t18" "t18" "t104" ...
#>  $ ord     : Ord.factor w/ 4 levels "1"<"2"<"3"<"4": 1 3 1 1 2 2 1 1 2 4 ...
#>  $ nom     : Factor w/ 3 levels "1","2","3": 3 1 3 3 3 2 2 2 1 3 ...
#>  $ con     : num  -0.0441 0.3153 0.2793 -0.3384 -0.3122 ...
#>  $ fvt     :List of 384
#>   ..$ : num  1.002 0.989 0.988 0.937 0.881 ...
#>   ..$ : num  0.981 1 0.972 0.947 0.86 ...
#>   ..$ : num  0.979 1.004 0.981 0.933 0.868 ...
#>   ..$ : num  1.007 0.982 0.938 0.85 0.671 ...
#>   ..$ : num  0.997 0.987 0.938 0.837 0.679 ...
#>   .. [list output truncated]

Our analysis requires a data frame where each row consists of an id variable alongside a $D$ -dimensional vector of traits.

manifest_trait_df <- cbind(synthetic_traits[, 1:4], fvt = t(simplify2array(synthetic_traits$fvt)))

The first step required for CAVI is to specify metadata for the manifest traits using the specify_manifest_trait_metadata function. This function allows the user to specify the specific properties of a particular data set and, given the data frame containing manifest traits, performs a number of tests to verify that the metadata matches the manifest traits.

# ?specify_manifest_trait_metadata
metadata <- specify_manifest_trait_metadata(
  n_traits = 4,
  trait_names = colnames(synthetic_traits)[-1],
  trait_type = factor(c("ord", "nom", "con", "fvt")),
  trait_levels = c(
    nlevels(manifest_trait_df$ord), nlevels(manifest_trait_df$nom),
    NA, NA
    ),
  manifest_trait_index = list(
    ord = 2, nom = 3, con = 4, fvt = 4 + 1:32
  ),
  auxiliary_trait_index = list(
    ord = 1, nom = 1 + 1:3, con = 5, fvt = 5 + 1:32
  ),
  link_functions = list(
    ord = ordinal_link, nom = nominal_link, con = function(x) x, fvt = function(x) exp(x)
  ),
  inverse_link_functions = list(
    ord = function(y){
      ordinal_inverse_link(
        y, cut_off_points = metadata$cut_off_points$ord,
        mu = rep(0, nrow(manifest_trait_df)), return_expectation = FALSE
      )
    },
    nom = function(y){
      nominal_inverse_link(
        y, mu = matrix(0, nrow(manifest_trait_df), length(metadata$categories$nom)),
        n_samples = 1000, return_expectation = FALSE
      )
    },
    con = function(y) y,
    fvt = function(y) log(data.matrix(y))
  ),
  cut_off_points = list(
    ord = c(-Inf, 0, sort(runif(nlevels(manifest_trait_df$ord) - 2)), Inf),
    nom = NA, con = NA, fvt = NA
  ),
  categories = list(
    ord = NA, nom = levels(manifest_trait_df$nom),
    con = NA, fvt = NA
  ),
  manifest_trait_df = manifest_trait_df,
  perform_checks = TRUE
)

Note that the exponential link function for fvt maps real valued auxiliary traits to positive real valued manifest traits. In addition, the link functions specified here are only required to initialise the PLVM. CAVI will allow the

Given the metadata, we are now ready to initialise a PLVM using initialise_plvm. This requires the phylogeny of evolutionary relationships between extant taxa, the dimension of the latent trait, and a prior correlation structure for the columns of the PLVM Loading.

# ?initialise_plvm
L <- 3
C_w <- metadata$auxiliary_trait_index %>% 
  unlist() %>% 
  length() %>% 
  diag()
x_fvt <- seq(0, 1, length.out = length(metadata$auxiliary_trait_index$fvt))
d <- abs(outer(x_fvt, x_fvt, "-"))
ell <- 1 / (2 * pi) # Length-scale to be specified by the user
C_w[metadata$auxiliary_trait_index$fvt, metadata$auxiliary_trait_index$fvt] <- (exp_quad_kernel(d, 1, ell) + (1e-6 * diag(length(x_fvt)))) / (1 + 1e-6)


plvm <- initialise_plvm(
  manifest_trait_df = manifest_trait_df, 
  metadata = metadata, 
  L = L,
  phy = synthetic_trait_model_specification$phylogeny,
  id_label = "taxon_id",
  loading_prior_correlation = C_w)

This is the minimum required specification for vbar to initialise a PLVM. By default, auxiliary traits are sampled at random given the initial ordinal trait cut-off points and discrete manifest traits. Varimax analysis of the resulting auxiliary traits provide sensible initial values for the PLVM Loading. All the remaining parameters and latent variables are then sampled at random.

Given an initial PLVM, we can implement CAVI using the cavi_plvm function. In the interest of brevity, the CAVI algorithm is run for 10 iterations only. For empirical data problems we would iterate to convergence of the ELBO, defined by tol.

cavi <- cavi_plvm(
  plvm_list = plvm,
  tol = 1e-1, max_iter = 10,
  n_samples = 1000, random_seed = 202,
  progress_bar = TRUE,
  perform_checks = FALSE
)
#>   |                                                                              |                                                                      |   0%  |                                                                              |=======                                                               |  10%  |                                                                              |==============                                                        |  20%  |                                                                              |=====================                                                 |  30%  |                                                                              |============================                                          |  40%  |                                                                              |===================================                                   |  50%  |                                                                              |==========================================                            |  60%  |                                                                              |=================================================                     |  70%  |                                                                              |========================================================              |  80%  |                                                                              |===============================================================       |  90%  |                                                                              |======================================================================| 100%

We can compare the output from the CAVI for the PLVM with the known parameters of the generative model.

First, we verify that the CAVI algorithm is maximising the ELBO. The figure omits the ELBO at the first 5 iterations of the CAVI for clarity.

We then account of any reordering or reflection of the inferred loadings relative to the true model specification.

R_mat <- IMIFA::Procrustes(
  cavi$model$loading_expectation,
  synthetic_trait_model_specification$loading
)$R %>% round

We can then compare inferred loadings (error bars and dotted lines) to the model specification (points and solid lines). This allows us to verify that

These are broadly similar, although the uncertainty intervals do not necessarily cover the model specification. There are a number of reasons for this. Variational Inference systematically underestimate uncertainty, and it can be difficult to infer loadings for discrete traits. The most relevant issue however, is that $\boldsymbol W$ and $\boldsymbol Z$ are non-identifiable in this model and so the output from CAVI is sensitive to initial values.

The primary goal of fitting this model to data is to perform Ancestral Reconstruction and so we will compare the approximate distribution for ancestral traits to those specified by the model. We examine the ancestral reconstruction of the ancestor at node 130 of the phylogeny. This is the same node for which the true ancestral distributions are presented above.

a <- 130
approx_ar <- variational_ancestral_reconstruction(
  taxon_specific_latent_trait_expectation = cavi$model$taxon_specific_latent_trait_expectation[a, ],
  taxon_specific_latent_trait_covariance = cavi$model$taxon_specific_latent_trait_covariance[a, ],
  loading_expectation = cavi$model$loading_expectation,
  precision_vector = cavi$model$precision_vector,
  metadata = cavi$model$metadata
)

Comparing this approximation to the true ancestral distribution, we find that they are broadly similar, although the approximate Bayesian inference scheme will tend to underestimate the uncertainty associated with ancestral traits.

The Co-ordinate Ascent Variational Inference scheme for approximate Bayesian inference on a generalised Phylogenetic Latent Variable Model provides estimates for the ancestral distribution of any collection of discrete and continuous traits.

jpmeagher/vbar documentation built on Nov. 22, 2022, 5:48 a.m.

rdrr.io home R language documentation Run R code online

CRAN packages Bioconductor packages R-Forge packages GitHub packages

Note that we can't provide technical support on individual packages. You should contact the package authors for that.

Tweet to @rdrrHQ

GitHub issue tracker

ian@mutexlabs.com