In riatelab/fisheye: Transform Base Maps Using Log-Azimuthal Projection
knitr::opts_chunk$set(
collapse = TRUE,
comment = "#>",
fig.path = "man/figures/README-",
out.width = "100%"
)
fisheye 
The goal of fisheye is to create base maps focusing on a specific location using an azimuthal logarithmic distance transformation.

John Bachmann, New York and environs, 1859.
Installation
You can install the released version of fisheye from
CRAN with:
install.packages("fisheye")
Alternatively, you can install the development version of fisheye from
GitHub with:
remotes::install_github("riatelab/fisheye")
Example
This is a basic example:
library(sf)
library(fisheye)
library(mapsf)
# Import dataset
ncraw <- st_read(system.file("shape/nc.shp", package="sf"), quiet = TRUE)
nc <- st_transform(ncraw, 3857)
par(mfrow = c(1,2))
mf_map(nc, col ="grey90")
mf_map(nc[51, ], add = TRUE, col = "grey40")
mf_title("Original Map")
# transform the basemap
nc_fe <- fisheye(nc, centre = nc[51, ])
mf_map(nc_fe, col ="grey90")
mf_map(nc_fe[51, ], add = TRUE, col = "grey40")
mf_title("Log-Azimuthal Projection")
# data import
par(mfrow = c(1,2))
mf_theme(mar = c(0.5,0.5,0.5,0.5))
center <- st_centroid(st_geometry(nc[51, ]))
buf_size <- c(
seq(100,1000, 100),
seq(1000,10000,1000),
seq(10000, 100000, 10000)
)
lb <- vector("list", length(buf_size))
for (i in seq_along(lb)){
lb[[i]] <- st_buffer(center, buf_size[i])
}
buf <- st_sf(geom = do.call(c, lb))
mf_init(nc)
mf_map(nc, col ="grey90", border = "white", add = TRUE)
mf_map(buf, add = TRUE, border = "red", col = NA, lwd = .4, lty = 3)
mf_map(buf[c(10,20,30), ], add = TRUE, border = "red", col = NA,
lwd = 1, lty = 1)
mf_map(center, pch = 20, add = TRUE)
for (i in c(20, 30)){
text(x = st_coordinates(center)[1,1],
y = st_bbox(buf[i, ])[4],
labels = paste0(round(buf_size[i]/1000, 0), "km")
)
}
buffe <- fisheye(buf, centre = center, method = "log", k = 1)
ncfe <- fisheye(nc, centre = center, method = "log", k = 1)
mf_init(buffe)
mf_map(ncfe, add = TRUE)
mf_map(buffe, add = TRUE, border = "red", col = NA, lwd = .4, lty = 3)
mf_map(buffe[c(1,10,20,30), ], add = TRUE, border = "red", col = NA,
lwd = 1, lty = 1)
points(0,0,pch = 20)
for (i in c(1,10,20,30)){
text(x = 0,
y = st_bbox(buffe[i, ])[4],
labels = paste0(signif(buf_size[i]/1000, 0), "km")
)
}
See a more detailed example here:
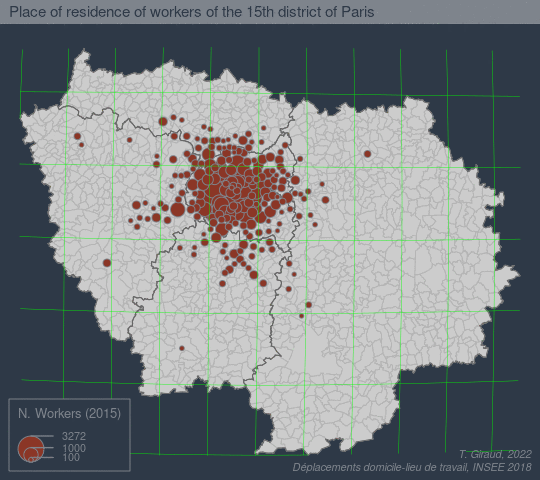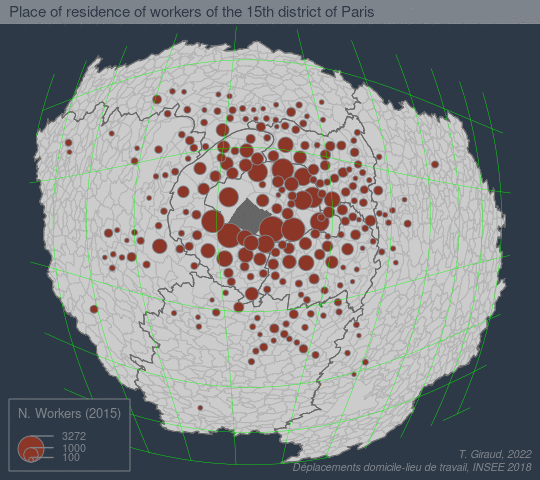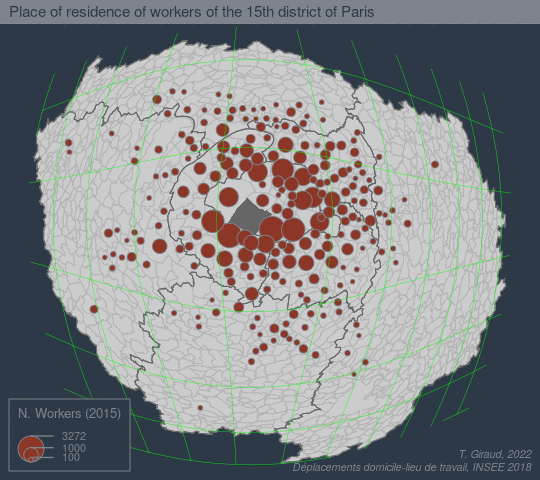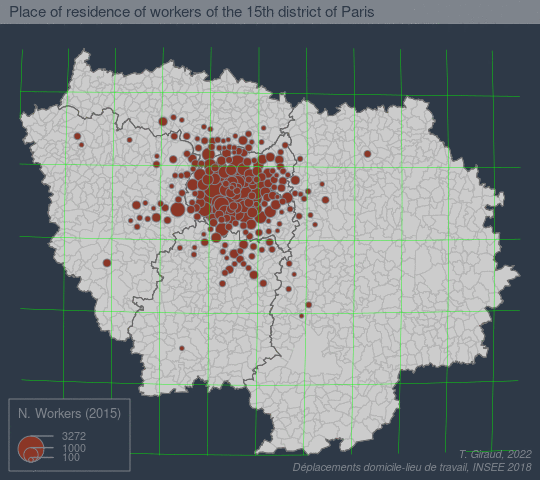
References
-
Hägerstrand, T. (1957). Migration and Area: A Survey of a Sample of Swedish Migration Fields and Hypothetical Considerations of their Genesis. Lund Studies in Geography, Series B, Human Geography, Department of Geography, University of Lund, Lund.
-
Snyder, J.P. (1987). "Magnifying-Glass" Azimuthal Map Projections. The American Cartographer, 14:1, 61-68, https://doi.org/10.1559/152304087783875318
-
Fairbairn, D., & Taylor, G. (1995). Developing a variable-scale map projection for urban areas. Computers & Geosciences, 21:9, 1053-1064, https://doi.org/10.1016/0098-3004(95)00041-6
-
Boutoura, C., Tsioukas, V., & Tsorlini, A. (2012). Experimenting “fisheye-lens functions” in studying digitally particular historic maps. e-Perimetron (ISSN 1790 - 3769). 7. 111-123. http://www.e-perimetron.org/Vol_7_3/Boutoura_et_al.pdf
-
Roughan, M. (2017). Log-azimuthal maps. https://roughan.info/math/log-az/
-
Rivière, P. (2018). The Log-Azimuthal projection. https://observablehq.com/@fil/log-azimuthal
-
Jansen, T. (2018). “Magnifying-Glass” projections. https://observablehq.com/@toja/magnifying-glass-projections
-
Sahasrabuddhe, R., Lambiotte, R., & Alessandretti, L. (2021). From centre to centres: polycentric structures in individual mobility. https://arxiv.org/pdf/2108.08113.pdf
riatelab/fisheye documentation built on May 2, 2024, 11:04 a.m.
knitr::opts_chunk$set( collapse = TRUE, comment = "#>", fig.path = "man/figures/README-", out.width = "100%" )
fisheye 
The goal of fisheye is to create base maps focusing on a specific location using an azimuthal logarithmic distance transformation.

John Bachmann, New York and environs, 1859.
Installation
You can install the released version of fisheye from
CRAN with:
install.packages("fisheye")
Alternatively, you can install the development version of fisheye from
GitHub with:
remotes::install_github("riatelab/fisheye")
Example
This is a basic example:
library(sf) library(fisheye) library(mapsf) # Import dataset ncraw <- st_read(system.file("shape/nc.shp", package="sf"), quiet = TRUE) nc <- st_transform(ncraw, 3857) par(mfrow = c(1,2)) mf_map(nc, col ="grey90") mf_map(nc[51, ], add = TRUE, col = "grey40") mf_title("Original Map") # transform the basemap nc_fe <- fisheye(nc, centre = nc[51, ]) mf_map(nc_fe, col ="grey90") mf_map(nc_fe[51, ], add = TRUE, col = "grey40") mf_title("Log-Azimuthal Projection")
# data import par(mfrow = c(1,2)) mf_theme(mar = c(0.5,0.5,0.5,0.5)) center <- st_centroid(st_geometry(nc[51, ])) buf_size <- c( seq(100,1000, 100), seq(1000,10000,1000), seq(10000, 100000, 10000) ) lb <- vector("list", length(buf_size)) for (i in seq_along(lb)){ lb[[i]] <- st_buffer(center, buf_size[i]) } buf <- st_sf(geom = do.call(c, lb)) mf_init(nc) mf_map(nc, col ="grey90", border = "white", add = TRUE) mf_map(buf, add = TRUE, border = "red", col = NA, lwd = .4, lty = 3) mf_map(buf[c(10,20,30), ], add = TRUE, border = "red", col = NA, lwd = 1, lty = 1) mf_map(center, pch = 20, add = TRUE) for (i in c(20, 30)){ text(x = st_coordinates(center)[1,1], y = st_bbox(buf[i, ])[4], labels = paste0(round(buf_size[i]/1000, 0), "km") ) } buffe <- fisheye(buf, centre = center, method = "log", k = 1) ncfe <- fisheye(nc, centre = center, method = "log", k = 1) mf_init(buffe) mf_map(ncfe, add = TRUE) mf_map(buffe, add = TRUE, border = "red", col = NA, lwd = .4, lty = 3) mf_map(buffe[c(1,10,20,30), ], add = TRUE, border = "red", col = NA, lwd = 1, lty = 1) points(0,0,pch = 20) for (i in c(1,10,20,30)){ text(x = 0, y = st_bbox(buffe[i, ])[4], labels = paste0(signif(buf_size[i]/1000, 0), "km") ) }
See a more detailed example here:

References
-
Hägerstrand, T. (1957). Migration and Area: A Survey of a Sample of Swedish Migration Fields and Hypothetical Considerations of their Genesis. Lund Studies in Geography, Series B, Human Geography, Department of Geography, University of Lund, Lund.
-
Snyder, J.P. (1987). "Magnifying-Glass" Azimuthal Map Projections. The American Cartographer, 14:1, 61-68, https://doi.org/10.1559/152304087783875318
-
Fairbairn, D., & Taylor, G. (1995). Developing a variable-scale map projection for urban areas. Computers & Geosciences, 21:9, 1053-1064, https://doi.org/10.1016/0098-3004(95)00041-6
-
Boutoura, C., Tsioukas, V., & Tsorlini, A. (2012). Experimenting “fisheye-lens functions” in studying digitally particular historic maps. e-Perimetron (ISSN 1790 - 3769). 7. 111-123. http://www.e-perimetron.org/Vol_7_3/Boutoura_et_al.pdf
-
Roughan, M. (2017). Log-azimuthal maps. https://roughan.info/math/log-az/
-
Rivière, P. (2018). The Log-Azimuthal projection. https://observablehq.com/@fil/log-azimuthal
-
Jansen, T. (2018). “Magnifying-Glass” projections. https://observablehq.com/@toja/magnifying-glass-projections
-
Sahasrabuddhe, R., Lambiotte, R., & Alessandretti, L. (2021). From centre to centres: polycentric structures in individual mobility. https://arxiv.org/pdf/2108.08113.pdf
Add the following code to your website.
For more information on customizing the embed code, read Embedding Snippets.
