README.md
In allanecology/BetaDivMultifun: Testing effects of multitrophic beta-diversity and land-use intensity (LUI) on ecosystem multifunctionality
create random conflict from desktop
BetaDivMultifun
The goal of BetaDivMultifun is to …
Installation
For installation, please consider the vignette
how-to-use-this-package.Rmd.
Install the development version from GitHub with:
# install.packages("devtools")
devtools::install_github("allanecology/BetaDivMultifun")
Content
- The scripts you need are in the folder vignettes
#TODO : - add a content description (TOC) - add the script overview
image
Example
This is a basic example which shows you how to solve a common problem:
library(BetaDivMultifun)
## basic example code
You’ll still need to render README.Rmd regularly, to keep README.md
up-to-date. devtools::build_readme() is handy for this. You could also
use GitHub Actions to re-render README.Rmd every time you push. An
example workflow can be found here:
https://github.com/r-lib/actions/tree/master/examples.
You can also embed plots, for example:

In that case, don’t forget to commit and push the resulting figure
files, so they display on GitHub and CRAN.
creating assembled_functions dataset
is described in 3 scripts in another github folder :
https://github.com/biodiversity-exploratories-synthesis/2019_grassland_functions
In this package, the required dataset is just read in and an analysis is
performed. As the dataset was constructed from within this directory,
the commits can be looked up here.
After installing the package and being connected to the “planteco” drive
at IPS: * find the file nonpublic.R, it is stored at the “planteco”
drive where the data is. * run nonpublic.R * run
1read_raw_datasets.Rmd then 2calc_raw_dataset.R * the file
"~/Desktop/december2018_assembled_functions_dataset.csv" will be
written on your Desktop.
Betadiversity formulae
After Baselga 2010, Global Ecology and Biogeography
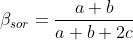
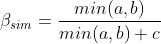
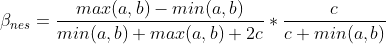
allanecology/BetaDivMultifun documentation built on Nov. 9, 2023, 8:47 p.m.
create random conflict from desktop
BetaDivMultifun
The goal of BetaDivMultifun is to …
Installation
For installation, please consider the vignette
how-to-use-this-package.Rmd.
Install the development version from GitHub with:
# install.packages("devtools")
devtools::install_github("allanecology/BetaDivMultifun")
Content
- The scripts you need are in the folder vignettes
#TODO : - add a content description (TOC) - add the script overview image
Example
This is a basic example which shows you how to solve a common problem:
library(BetaDivMultifun)
## basic example code
You’ll still need to render README.Rmd regularly, to keep README.md
up-to-date. devtools::build_readme() is handy for this. You could also
use GitHub Actions to re-render README.Rmd every time you push. An
example workflow can be found here:
https://github.com/r-lib/actions/tree/master/examples.
You can also embed plots, for example:

In that case, don’t forget to commit and push the resulting figure files, so they display on GitHub and CRAN.
creating assembled_functions dataset
is described in 3 scripts in another github folder : https://github.com/biodiversity-exploratories-synthesis/2019_grassland_functions
In this package, the required dataset is just read in and an analysis is performed. As the dataset was constructed from within this directory, the commits can be looked up here.
After installing the package and being connected to the “planteco” drive
at IPS: * find the file nonpublic.R, it is stored at the “planteco”
drive where the data is. * run nonpublic.R * run
1read_raw_datasets.Rmd then 2calc_raw_dataset.R * the file
"~/Desktop/december2018_assembled_functions_dataset.csv" will be
written on your Desktop.
Betadiversity formulae
After Baselga 2010, Global Ecology and Biogeography
Add the following code to your website.
For more information on customizing the embed code, read Embedding Snippets.
