README.md
In juhokalle/rmfd4dfm: Estimation of DFMs using RMFD-E parametrization
Estimation of Impulse-Response Functions with Dynamic Factor Models: A
New Parametrization
================
This repository contains the associated R-package and data to the paper
Estimation of Impulse-Response Functions with Dynamic Factor Models: A
New Parametrization authored by Juho
Koistinen and Bernd
Funovits (2022).
Specifically, the functions within the package allow the user to
estimate a structural dynamic factor model (DFM), with the common
component parametrized as a right matrix fraction description in echelon
form (RMFD-E), which is introduced in Section
2.2 of the
associated paper. This document also shows how to replicate the
empirical exercise of Section
4.
The package builds on the R-packages rationalmatrices and RLDM,
authored by Bernd Funovits and Wolfgang Scherrer. Since these packages
might change, the parts which are necessary for the analysis in the
associated article are extracted to R files \~/rmfd4dfm/R/zz_ratmat
and \~/rmfd4dfm/R/zz_rldm. Importantly, please reference the
rationalmatrices and the RLDM packages should you use their
functionalities and not this package.
Installation
The package can be installed using the following command as is the
standard with packages hosted by GitHub.
# install.packages("devtools")
devtools::install_github("juhokalle/rmfd4dfm")
The Model and Argument
Here I will provide a brief and hopefully accessible introduction to the
modelling approach presented in the paper, while the details are
available from the paper. The aim is to identify and estimate
impulse-response functions (IRFs) using dynamic factor models (DFMs),
with the emphasis placed on macroeconomic applications and analysis. The
model of interest is given as



where
 is an
is an
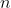 -dimensional
observed time series, with usually
-dimensional
observed time series, with usually
 .
. is a
is a
 -dimensional
dynamic factor process, with usually
-dimensional
dynamic factor process, with usually
 .
. is an
is an
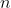 -dimensional
idiosyncratic term, we assume
-dimensional
idiosyncratic term, we assume
 .
. is the innovation to
is the innovation to
 ,
with
,
with
 .
. and
and
 are
are
 and
and
 parameter matrices, values of which are at the center of interest as
the IRFs are constructed from these matrices.
parameter matrices, values of which are at the center of interest as
the IRFs are constructed from these matrices. is the
is the
 -dimensional
structural shock process, with
-dimensional
structural shock process, with
 .
. is
is
 -dimensional
structural impact multiplier matrix, which we identify as
-dimensional
structural impact multiplier matrix, which we identify as
 ,
where
,
where
 is the lower triangular Cholesky factor of
is the lower triangular Cholesky factor of
 .
Note that any other identification method for uncovering
.
Note that any other identification method for uncovering
 is valid as in the structural vector autoregression (SVAR) analysis.
is valid as in the structural vector autoregression (SVAR) analysis.
We can write Eq. (2) compactly as
 and substitute this and Eq. (3) into Eq. (1) to get
and substitute this and Eq. (3) into Eq. (1) to get

where

and

If we assume that the idiosyncratic component accounts for measurements
errors or sectoral dynamics that pertain to a small number of variables,
we can use the structural IRF
 to study the shock propagation from
to study the shock propagation from
 structural shocks to
structural shocks to
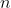 observed macroeconomic variables, with
observed macroeconomic variables, with
 .
The IRF
.
The IRF
 is not identified without further restrictions since one can always
post-multiply
is not identified without further restrictions since one can always
post-multiply
 and
and
 by some
by some
 polynomial matrix
polynomial matrix
 such that it “cancels out”:
such that it “cancels out”:
![k(L)=d(L)c(L)^{-1}=[d(L)m(L)][c(L)m(L)]^{-1}=\bar d(L) \bar c(L)^{-1}.](https://latex.codecogs.com/png.image?%5Cdpi%7B110%7D&space;%5Cbg_white&space;%0Ak%28L%29%3Dd%28L%29c%28L%29%5E%7B-1%7D%3D%5Bd%28L%29m%28L%29%5D%5Bc%28L%29m%28L%29%5D%5E%7B-1%7D%3D%5Cbar%20d%28L%29%20%5Cbar%20c%28L%29%5E%7B-1%7D.%0A)
The problem is that the researcher cannot distinguish between
 and
and
 from the first and second moments of the data, and therefore attempts at
drawing conclusions from the structural IRF
from the first and second moments of the data, and therefore attempts at
drawing conclusions from the structural IRF
 are futile without further assumptions on
are futile without further assumptions on
 and
and
 .
.
Our insight is that
 can be identified, that is, the set of matrices
can be identified, that is, the set of matrices
 can be narrowed down to
can be narrowed down to
 ,
using the identification restrictions that are standard in the
literature dealing with the identification of the vector autoregressive
moving average (VARMA) models (for a recent summary, see Deistler and
Scherrer,
2019).
In this model class, the IRF is given as
,
using the identification restrictions that are standard in the
literature dealing with the identification of the vector autoregressive
moving average (VARMA) models (for a recent summary, see Deistler and
Scherrer,
2019).
In this model class, the IRF is given as
 for some AR and MA lag polynomials
for some AR and MA lag polynomials
 and
and
 of suitable dimensions, and here
of suitable dimensions, and here
 and
and
 can be pre-multiplied by some lag polynomial
can be pre-multiplied by some lag polynomial
 to obtain an observationally equivalent IRF:
to obtain an observationally equivalent IRF:
![k(L)=a(L)^{-1}b(L)=[m(L)a(L)]^{-1}[m(L)b(L)]=\bar a(L)^{-1}\bar b(L).](https://latex.codecogs.com/png.image?%5Cdpi%7B110%7D&space;%5Cbg_white&space;%0Ak%28L%29%3Da%28L%29%5E%7B-1%7Db%28L%29%3D%5Bm%28L%29a%28L%29%5D%5E%7B-1%7D%5Bm%28L%29b%28L%29%5D%3D%5Cbar%20a%28L%29%5E%7B-1%7D%5Cbar%20b%28L%29.%0A)
One popular identification approach for the VARMA model is to use the
canonical echelon form parametrization, which involves zero and unity
restrictions in
 and
and
 .
By noting that the identification restrictions for the IRF in right
matrix fraction description (RMFD, for short) model,
i.e.
.
By noting that the identification restrictions for the IRF in right
matrix fraction description (RMFD, for short) model,
i.e.  ,
are equivalent to those for the VARMA model after transposing, the
derivation is quite straightforward using the existing results for the
VARMA model (for details, see Appendix
A).
,
are equivalent to those for the VARMA model after transposing, the
derivation is quite straightforward using the existing results for the
VARMA model (for details, see Appendix
A).
The structure of the RMFD model in echelon form is quite complicated,
and while the functions of this package rmfd4dfm code these
restrictions without the need for the user to trouble herself with the
implementation, one might still wonder what is the point of going
through the painstaking process of deriving and coding the restrictions
in the first place, as there are alternatives in the literature? To make
the point, let us introduce a popular alternative used in the literature
and compare it with our approach. One way to deal with the
identification and estimation of the DFM presented above is to stack the
dynamic factors into a
 -dimensional
vector
-dimensional
vector

and write Eq. (1) as

which makes the model amenable to the principal components (PC) methods.
In the second step, the static factor process is modelled as a
VAR(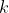 )
process
)
process

where
 is an
is an
 VAR lag polynomial of order
VAR lag polynomial of order
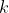 ,
and
,
and
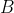 is an
is an
 constant matrix. After the estimation of
constant matrix. After the estimation of
 and
and
 ,
the IRF
,
the IRF
 can be constructed straightforwardly.
can be constructed straightforwardly.
This alternative using PCs is straightforward from an estimation point
of view, but let us point two associated restrictive features. First,
note that the minimal number of identifying restrictions needed is
 ,
which is higher than that of in our parametrization,
i.e.
,
which is higher than that of in our parametrization,
i.e.  ,
whenever
,
whenever
 (Bai and Wang,
2012).
Second, we note that the reliable estimation of VAR on
(Bai and Wang,
2012).
Second, we note that the reliable estimation of VAR on
 can be difficult if the lag order is misspecified, which is due to the
singularity of the covariance matrix of the innovation to
can be difficult if the lag order is misspecified, which is due to the
singularity of the covariance matrix of the innovation to
 ,
i.e.
,
i.e.
 has rank
has rank
 ,
which is smaller than
,
which is smaller than
 if
if
 (Hörmann and Nisol,
2021). On
the other hand, the law of motion for
(Hörmann and Nisol,
2021). On
the other hand, the law of motion for
 is standard non-singular VAR in our setup. These two examples make the
case that the “static” method is suboptimal whenever
is standard non-singular VAR in our setup. These two examples make the
case that the “static” method is suboptimal whenever
 and warrant considering other alternatives, development of which is the
main goal of our paper.
and warrant considering other alternatives, development of which is the
main goal of our paper.
Data
The package makes available three different macroeconomic panels of data
measured at a monthly frequency. First is the data used by Forni and
Gambetti
(2010),
and the documentation can be accessed using command ?FG_data in the R
console. Second and third data sets, FRED_light and FRED_heavy
originate from the FRED-MD data set, which is documented carefully in
McCracken and Ng
(2015).
The difference between the data sets concerns the transformations to
obtain stationarity, while the time span is same in both data sets to
facilitate comparison to Forni and Gambetti
(2010).
The details can be accessed by ?FRED_light or ?FRED_heavy.
Replication of the Monetary Policy Example
The empirical example compares the DFMs estimated by Forni and Gambetti
(2010)
to that developed in our paper. The idea is to assess the effects of
monetary policy to key macroeconomic variables via structural DFMs,
which guards against the omitted variable bias, to which the SVAR
methods can be more susceptible.
The following code snippets show how to replicate the results given in
the empirical section of our paper. First, we order the variables of
interest in the structural analysis variables first in the data matrix,
i.e. industrial production (INDPRO, the mnemonic in McCracken and Ng,
2015),
consumer price index (CPIAUCSL), federal funds rate (FEDFUNDS), and real
Swiss/US exchange rate (EXSZUSx), in this order. In the structural
analysis with recursive identification, the ordering is important, as it
determines the short-run restrictions imposed on the structural impact
multiplier matrix. (For a brief and to the point summary of the
structural identification using DFMs, see Section
9 of
the lecture notes written by Matteo
Barigozzi.) Additionally, one must
include a vector int_ix in the data object FRED_heavy coding the
positions of the variables of interest, which in this case is simply a
sequence 1:4.
library("rmfd4dfm")
# code the positions of the variables of interest
int_vars_fred <- c("INDPRO", "CPIAUCSL", "FEDFUNDS", "EXSZUSx")
int_ix <- sapply(int_vars_fred, function(x) which(names(FRED_heavy$df)==x))
# re-organize data matrix s.t. the variables of interest are ordered first
perm_ix <- c(int_ix, (1:ncol(FRED_heavy$df))[-int_ix])
FRED_heavy$df <- FRED_heavy$df[,perm_ix]
FRED_heavy$trans_ix <- FRED_heavy$trans_ix[perm_ix]
FRED_heavy$int_ix <- 1:4
Second, we need to determine the static factor dimension. This is needed
for an estimate of the lag structure in eqs. (1)–(2), while in the
“static” method it defines the dimension of
 .
To this end, we use functions
.
To this end, we use functions baingcriterion and abc_crit, which
implement the tests developed in Bai and Ng
(2002) and
Alessi, Barigozzi and Capasso
(2009),
respectively.
# Estimate the number of static factors ####
baing_cr <- baingcriterion(FRED_heavy$df, rmax = 25)$IC[1:2]
abc_cr <- replicate(50, abc_crit(FRED_heavy$df, kmax = 25))
get_mode <- function(x) unique(x)[which.max(colSums(sapply(unique(x), function(z) x %in% z)))]
r_hats <- c("ICp1" = baing_cr[1],
"ICp2" = baing_cr[2],
"ABCp1" = get_mode(unlist(abc_cr[1,])),
"ABCp2" = get_mode(unlist(abc_cr[2,]))
)
Upon fixing the state dimension of the state space representation of
eqs. (1)–(2), estimation of the DFM can be carried out. Here we fix the
static factor dimension to 8. In the RMFD-E parametrization of the DFM
and for a given state dimension, it is likely that one has many model
specifications available from which to choose “the best model”.
Therefore, the function do_everything_rmfd estimates all the model
alternatives that are consistent with the model selection criteria given
in Section 3.3.
and chooses the one that minimizes Bayesian information criterion. For
this model, the function then estimates confidence intervals for the IRF
using block bootstrap. Finally, the function returns the impulse
responses of the variables to the third shock, which is standardized to
have an immediate impact of 0.5. For responses to other shocks and/or
size, one can include an index vector of length two, which specifies the
shock of interest and normalization constant, in the data object
specified as the first argument of do_everything_rmfd by
df$shock_ix. For a more flexible estimation setup, the user can
consult function estim_wrap, which produces an estimate of the
non-structural IRF
 for a given model structure. The functions
for a given model structure. The functions do_everything_fglr and
do_everything_svar perform the same task for the static DFM and
structural VAR, respectively.
# D-DFM
est_obj <- do_everything_rmfd(df = FRED_heavy,
r = 8,
h = 50,
nrep = 500,
conv_crit = 1e-5,
ci = 0.68,
init_rep = 1,
verbose = TRUE)
# S-DFM
est_fglr <- do_everything_fglr(df = FRED_heavy,
r = 8,
k = 2,
h = 50,
nrep = 500,
ci = 0.68)
# SVAR
svar_irf <- do_everything_svar(df = FRED_heavy,
p = 9,
nrep = 500,
h = 50,
ci = 0.68)
Finally, the plot_irfs function returns the IRFs along with the
possible error bands in a nice plot. To gather the IRF plots into one
figure, which can then be exported to pdf, for example, we use
gridExtra::marrangeGrob.
p1 <- plot_irfs(est_obj$irf, int_vars_fred, "D-DFM")
p2 <- plot_irfs(est_fglr, int_vars_fred, "S-DFM", label_y = FALSE)
p3 <- plot_irfs(svar_irf, int_vars_fred, "SVAR", label_y = FALSE)
plot1 <- gridExtra::marrangeGrob(c(p1,p2,p3), nrow = 4, ncol = 3, top = NULL)
juhokalle/rmfd4dfm documentation built on July 18, 2024, 10:19 p.m.
Estimation of Impulse-Response Functions with Dynamic Factor Models: A New Parametrization ================
This repository contains the associated R-package and data to the paper Estimation of Impulse-Response Functions with Dynamic Factor Models: A New Parametrization authored by Juho Koistinen and Bernd Funovits (2022). Specifically, the functions within the package allow the user to estimate a structural dynamic factor model (DFM), with the common component parametrized as a right matrix fraction description in echelon form (RMFD-E), which is introduced in Section 2.2 of the associated paper. This document also shows how to replicate the empirical exercise of Section 4.
The package builds on the R-packages rationalmatrices and RLDM, authored by Bernd Funovits and Wolfgang Scherrer. Since these packages might change, the parts which are necessary for the analysis in the associated article are extracted to R files \~/rmfd4dfm/R/zz_ratmat and \~/rmfd4dfm/R/zz_rldm. Importantly, please reference the rationalmatrices and the RLDM packages should you use their functionalities and not this package.
Installation
The package can be installed using the following command as is the standard with packages hosted by GitHub.
# install.packages("devtools")
devtools::install_github("juhokalle/rmfd4dfm")
The Model and Argument
Here I will provide a brief and hopefully accessible introduction to the modelling approach presented in the paper, while the details are available from the paper. The aim is to identify and estimate impulse-response functions (IRFs) using dynamic factor models (DFMs), with the emphasis placed on macroeconomic applications and analysis. The model of interest is given as
where
is an
-dimensional observed time series, with usually
.
is a
-dimensional dynamic factor process, with usually
.
is an
-dimensional idiosyncratic term, we assume
.
is the innovation to
, with
.
and
are
and
parameter matrices, values of which are at the center of interest as the IRFs are constructed from these matrices.
is the
-dimensional structural shock process, with
.
is
-dimensional structural impact multiplier matrix, which we identify as
, where
is the lower triangular Cholesky factor of
. Note that any other identification method for uncovering
is valid as in the structural vector autoregression (SVAR) analysis.
We can write Eq. (2) compactly as
and substitute this and Eq. (3) into Eq. (1) to get
where
and
If we assume that the idiosyncratic component accounts for measurements
errors or sectoral dynamics that pertain to a small number of variables,
we can use the structural IRF
to study the shock propagation from
structural shocks to
observed macroeconomic variables, with
.
The IRF
is not identified without further restrictions since one can always
post-multiply
and
by some
polynomial matrix
such that it “cancels out”:
The problem is that the researcher cannot distinguish between
and
from the first and second moments of the data, and therefore attempts at
drawing conclusions from the structural IRF
are futile without further assumptions on
and
.
Our insight is that
can be identified, that is, the set of matrices
can be narrowed down to
,
using the identification restrictions that are standard in the
literature dealing with the identification of the vector autoregressive
moving average (VARMA) models (for a recent summary, see Deistler and
Scherrer,
2019).
In this model class, the IRF is given as
for some AR and MA lag polynomials
and
of suitable dimensions, and here
and
can be pre-multiplied by some lag polynomial
to obtain an observationally equivalent IRF:
One popular identification approach for the VARMA model is to use the
canonical echelon form parametrization, which involves zero and unity
restrictions in
and
.
By noting that the identification restrictions for the IRF in right
matrix fraction description (RMFD, for short) model,
i.e.
,
are equivalent to those for the VARMA model after transposing, the
derivation is quite straightforward using the existing results for the
VARMA model (for details, see Appendix
A).
The structure of the RMFD model in echelon form is quite complicated,
and while the functions of this package rmfd4dfm code these
restrictions without the need for the user to trouble herself with the
implementation, one might still wonder what is the point of going
through the painstaking process of deriving and coding the restrictions
in the first place, as there are alternatives in the literature? To make
the point, let us introduce a popular alternative used in the literature
and compare it with our approach. One way to deal with the
identification and estimation of the DFM presented above is to stack the
dynamic factors into a
-dimensional
vector
and write Eq. (1) as
which makes the model amenable to the principal components (PC) methods.
In the second step, the static factor process is modelled as a
VAR()
process
where
is an
VAR lag polynomial of order
,
and
is an
constant matrix. After the estimation of
and
,
the IRF
can be constructed straightforwardly.
This alternative using PCs is straightforward from an estimation point
of view, but let us point two associated restrictive features. First,
note that the minimal number of identifying restrictions needed is
,
which is higher than that of in our parametrization,
i.e.
,
whenever
(Bai and Wang,
2012).
Second, we note that the reliable estimation of VAR on
can be difficult if the lag order is misspecified, which is due to the
singularity of the covariance matrix of the innovation to
,
i.e.
has rank
,
which is smaller than
if
(Hörmann and Nisol,
2021). On
the other hand, the law of motion for
is standard non-singular VAR in our setup. These two examples make the
case that the “static” method is suboptimal whenever
and warrant considering other alternatives, development of which is the
main goal of our paper.
Data
The package makes available three different macroeconomic panels of data
measured at a monthly frequency. First is the data used by Forni and
Gambetti
(2010),
and the documentation can be accessed using command ?FG_data in the R
console. Second and third data sets, FRED_light and FRED_heavy
originate from the FRED-MD data set, which is documented carefully in
McCracken and Ng
(2015).
The difference between the data sets concerns the transformations to
obtain stationarity, while the time span is same in both data sets to
facilitate comparison to Forni and Gambetti
(2010).
The details can be accessed by ?FRED_light or ?FRED_heavy.
Replication of the Monetary Policy Example
The empirical example compares the DFMs estimated by Forni and Gambetti (2010) to that developed in our paper. The idea is to assess the effects of monetary policy to key macroeconomic variables via structural DFMs, which guards against the omitted variable bias, to which the SVAR methods can be more susceptible.
The following code snippets show how to replicate the results given in
the empirical section of our paper. First, we order the variables of
interest in the structural analysis variables first in the data matrix,
i.e. industrial production (INDPRO, the mnemonic in McCracken and Ng,
2015),
consumer price index (CPIAUCSL), federal funds rate (FEDFUNDS), and real
Swiss/US exchange rate (EXSZUSx), in this order. In the structural
analysis with recursive identification, the ordering is important, as it
determines the short-run restrictions imposed on the structural impact
multiplier matrix. (For a brief and to the point summary of the
structural identification using DFMs, see Section
9 of
the lecture notes written by Matteo
Barigozzi.) Additionally, one must
include a vector int_ix in the data object FRED_heavy coding the
positions of the variables of interest, which in this case is simply a
sequence 1:4.
library("rmfd4dfm")
# code the positions of the variables of interest
int_vars_fred <- c("INDPRO", "CPIAUCSL", "FEDFUNDS", "EXSZUSx")
int_ix <- sapply(int_vars_fred, function(x) which(names(FRED_heavy$df)==x))
# re-organize data matrix s.t. the variables of interest are ordered first
perm_ix <- c(int_ix, (1:ncol(FRED_heavy$df))[-int_ix])
FRED_heavy$df <- FRED_heavy$df[,perm_ix]
FRED_heavy$trans_ix <- FRED_heavy$trans_ix[perm_ix]
FRED_heavy$int_ix <- 1:4
Second, we need to determine the static factor dimension. This is needed
for an estimate of the lag structure in eqs. (1)–(2), while in the
“static” method it defines the dimension of
.
To this end, we use functions
baingcriterion and abc_crit, which
implement the tests developed in Bai and Ng
(2002) and
Alessi, Barigozzi and Capasso
(2009),
respectively.
# Estimate the number of static factors ####
baing_cr <- baingcriterion(FRED_heavy$df, rmax = 25)$IC[1:2]
abc_cr <- replicate(50, abc_crit(FRED_heavy$df, kmax = 25))
get_mode <- function(x) unique(x)[which.max(colSums(sapply(unique(x), function(z) x %in% z)))]
r_hats <- c("ICp1" = baing_cr[1],
"ICp2" = baing_cr[2],
"ABCp1" = get_mode(unlist(abc_cr[1,])),
"ABCp2" = get_mode(unlist(abc_cr[2,]))
)
Upon fixing the state dimension of the state space representation of
eqs. (1)–(2), estimation of the DFM can be carried out. Here we fix the
static factor dimension to 8. In the RMFD-E parametrization of the DFM
and for a given state dimension, it is likely that one has many model
specifications available from which to choose “the best model”.
Therefore, the function do_everything_rmfd estimates all the model
alternatives that are consistent with the model selection criteria given
in Section 3.3.
and chooses the one that minimizes Bayesian information criterion. For
this model, the function then estimates confidence intervals for the IRF
using block bootstrap. Finally, the function returns the impulse
responses of the variables to the third shock, which is standardized to
have an immediate impact of 0.5. For responses to other shocks and/or
size, one can include an index vector of length two, which specifies the
shock of interest and normalization constant, in the data object
specified as the first argument of do_everything_rmfd by
df$shock_ix. For a more flexible estimation setup, the user can
consult function estim_wrap, which produces an estimate of the
non-structural IRF
for a given model structure. The functions
do_everything_fglr and
do_everything_svar perform the same task for the static DFM and
structural VAR, respectively.
# D-DFM
est_obj <- do_everything_rmfd(df = FRED_heavy,
r = 8,
h = 50,
nrep = 500,
conv_crit = 1e-5,
ci = 0.68,
init_rep = 1,
verbose = TRUE)
# S-DFM
est_fglr <- do_everything_fglr(df = FRED_heavy,
r = 8,
k = 2,
h = 50,
nrep = 500,
ci = 0.68)
# SVAR
svar_irf <- do_everything_svar(df = FRED_heavy,
p = 9,
nrep = 500,
h = 50,
ci = 0.68)
Finally, the plot_irfs function returns the IRFs along with the
possible error bands in a nice plot. To gather the IRF plots into one
figure, which can then be exported to pdf, for example, we use
gridExtra::marrangeGrob.
p1 <- plot_irfs(est_obj$irf, int_vars_fred, "D-DFM")
p2 <- plot_irfs(est_fglr, int_vars_fred, "S-DFM", label_y = FALSE)
p3 <- plot_irfs(svar_irf, int_vars_fred, "SVAR", label_y = FALSE)
plot1 <- gridExtra::marrangeGrob(c(p1,p2,p3), nrow = 4, ncol = 3, top = NULL)
Add the following code to your website.
For more information on customizing the embed code, read Embedding Snippets.
