README.md
In clifford: Arbitrary Dimensional Clifford Algebras
The clifford package: Clifford algebra in R

The clifford package provides R-centric functionality for working with
Clifford algebras of arbitrary dimension and signature. A detailed
vignette is provided in the package.
Installation
You can install the released version of the clifford package from
CRAN with:
# install.packages("clifford") # uncomment this to install the package
library("clifford")
set.seed(0)
The clifford package in use
The basic creation function is clifford(), which takes a list of basis
blades and a vector of coefficients:
(a <- clifford(list(1,2,1:4,2:3),1:4))
#> Element of a Clifford algebra, equal to
#> + 1e_1 + 2e_2 + 4e_23 + 3e_1234
(b <- clifford(list(2,2:3,1:2),c(-2,3,-3)))
#> Element of a Clifford algebra, equal to
#> - 2e_2 - 3e_12 + 3e_23
So a and b are multivectors. Clifford objects are a vector space and
we can add them using +:
a+b
#> Element of a Clifford algebra, equal to
#> + 1e_1 - 3e_12 + 7e_23 + 3e_1234
See how the e2 term vanishes and the e_23 term is summed. The
package includes a large number of products:
a*b # geometric product (also "a % % b")
#> Element of a Clifford algebra, equal to
#> - 16 + 6e_1 - 3e_2 - 2e_12 + 14e_3 + 12e_13 + 3e_123 - 9e_14 + 9e_34 - 6e_134
a %^% b # outer product
#> Element of a Clifford algebra, equal to
#> - 2e_12 + 3e_123
a %.% b # inner product
#> Element of a Clifford algebra, equal to
#> - 16 + 6e_1 - 3e_2 + 14e_3 - 9e_14 + 9e_34 - 6e_134
a %star% b # scalar product
#> [1] -16
a %euc% b # Euclidean product
#> [1] 8
The package can deal with non positive-definite inner products. Suppose
we wish to deal with an inner product of

where the diagonal is a number of
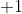 terms followed by
a number of
terms followed by
a number of 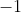 terms.
The package idiom for this would be to use
terms.
The package idiom for this would be to use signature():
signature(3)
Function signature() is based on lorentz::sol() and its argument
specifies the number of basis blades that square to
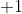 , the others
squaring to
, the others
squaring to 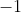 . Thus
. Thus
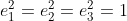 and
and
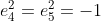 :
:
basis(1)
#> Element of a Clifford algebra, equal to
#> + 1e_1
basis(1)^2
#> Element of a Clifford algebra, equal to
#> scalar ( 1 )
basis(4)
#> Element of a Clifford algebra, equal to
#> + 1e_4
basis(4)^2
#> Element of a Clifford algebra, equal to
#> the zero clifford element (0)
The package uses the STL map class with dynamic bitset keys for
efficiency and speed and can deal with objects of arbitrary dimensions.
Thus:
options("basissep" = ",")
(x <- rcliff(d=20))
#> Element of a Clifford algebra, equal to
#> + 5 - 1e_2 + 6e_5 + 2e_4,7 - 3e_10 - 5e_11 + 3e_14 + 1e_10,14 + 4e_5,9,15 +
#> 9e_18,19
summary(x^3)
#> Element of a Clifford algebra
#> Typical terms: 140 ... + 216e_5,9,10,14,15,18,19
#> Number of terms: 44
#> Magnitude: 25376
References
- D. Hestenes 1987. Clifford algebra to geometric calculus, Kluwer.
- J. Snygg 2010. A new approach to differential geometry using
Clifford’s geometric algebra. Berghauser.
- C. Perwass 2009. Geometric algebra with applications in engineering.
Springer.
Further information
For more detail, see the package vignette
vignette("clifford")
Try the clifford package in your browser
Any scripts or data that you put into this service are public.
clifford documentation built on June 8, 2025, 10:56 a.m.
The clifford package: Clifford algebra in R

The clifford package provides R-centric functionality for working with
Clifford algebras of arbitrary dimension and signature. A detailed
vignette is provided in the package.
Installation
You can install the released version of the clifford package from CRAN with:
# install.packages("clifford") # uncomment this to install the package
library("clifford")
set.seed(0)
The clifford package in use
The basic creation function is clifford(), which takes a list of basis
blades and a vector of coefficients:
(a <- clifford(list(1,2,1:4,2:3),1:4))
#> Element of a Clifford algebra, equal to
#> + 1e_1 + 2e_2 + 4e_23 + 3e_1234
(b <- clifford(list(2,2:3,1:2),c(-2,3,-3)))
#> Element of a Clifford algebra, equal to
#> - 2e_2 - 3e_12 + 3e_23
So a and b are multivectors. Clifford objects are a vector space and
we can add them using +:
a+b
#> Element of a Clifford algebra, equal to
#> + 1e_1 - 3e_12 + 7e_23 + 3e_1234
See how the e2 term vanishes and the e_23 term is summed. The
package includes a large number of products:
a*b # geometric product (also "a % % b")
#> Element of a Clifford algebra, equal to
#> - 16 + 6e_1 - 3e_2 - 2e_12 + 14e_3 + 12e_13 + 3e_123 - 9e_14 + 9e_34 - 6e_134
a %^% b # outer product
#> Element of a Clifford algebra, equal to
#> - 2e_12 + 3e_123
a %.% b # inner product
#> Element of a Clifford algebra, equal to
#> - 16 + 6e_1 - 3e_2 + 14e_3 - 9e_14 + 9e_34 - 6e_134
a %star% b # scalar product
#> [1] -16
a %euc% b # Euclidean product
#> [1] 8
The package can deal with non positive-definite inner products. Suppose we wish to deal with an inner product of
where the diagonal is a number of
terms followed by
a number of
terms.
The package idiom for this would be to use
signature():
signature(3)
Function signature() is based on lorentz::sol() and its argument
specifies the number of basis blades that square to
, the others
squaring to
. Thus
and
:
basis(1)
#> Element of a Clifford algebra, equal to
#> + 1e_1
basis(1)^2
#> Element of a Clifford algebra, equal to
#> scalar ( 1 )
basis(4)
#> Element of a Clifford algebra, equal to
#> + 1e_4
basis(4)^2
#> Element of a Clifford algebra, equal to
#> the zero clifford element (0)
The package uses the STL map class with dynamic bitset keys for efficiency and speed and can deal with objects of arbitrary dimensions. Thus:
options("basissep" = ",")
(x <- rcliff(d=20))
#> Element of a Clifford algebra, equal to
#> + 5 - 1e_2 + 6e_5 + 2e_4,7 - 3e_10 - 5e_11 + 3e_14 + 1e_10,14 + 4e_5,9,15 +
#> 9e_18,19
summary(x^3)
#> Element of a Clifford algebra
#> Typical terms: 140 ... + 216e_5,9,10,14,15,18,19
#> Number of terms: 44
#> Magnitude: 25376
References
- D. Hestenes 1987. Clifford algebra to geometric calculus, Kluwer.
- J. Snygg 2010. A new approach to differential geometry using Clifford’s geometric algebra. Berghauser.
- C. Perwass 2009. Geometric algebra with applications in engineering. Springer.
Further information
For more detail, see the package vignette
vignette("clifford")
Try the clifford package in your browser
Any scripts or data that you put into this service are public.
Add the following code to your website.
For more information on customizing the embed code, read Embedding Snippets.
