README.md
In aliaksah/EMJMCMC2016: EMJMCMC
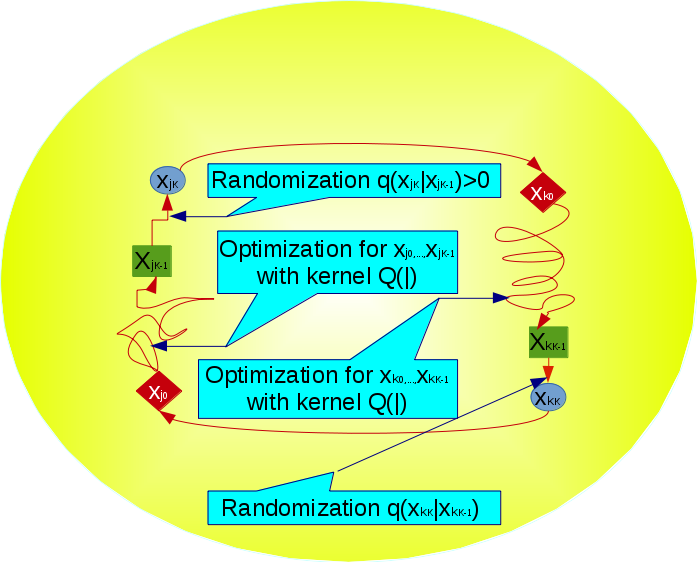
In this R package problems of Bayesian model selection and model averaging are addressed in various complex regression contexts. The approaches developed within the package are based on the idea of marginalizing out parameters from the likelihood. This allows to work on the marginal space of models, which simplifies the search algorithms significantly. For the generalized linear mixed models an efficient mode jumping Monte Carlo Markov chain (MJMCMC) algorithm is implemented. The approach performs very well on simulated and real data. Further, the algorithm is extended to work with logic regressions, where one has a feature space consisting of various complicated logical expressions, which makes enumeration of all features computationally and memory infeasible in most of the cases. The genetically modified MJMCMC (GMJMCMC) algorithm is suggested to tackle this issue. The algorithm combines the idea of keeping and updating the populations of highly predictive logical expressions combined with MJMCMC for the efficient exploration of the model space. Several simulation and real data studies show that logical expressions of high orders can be recovered with large power and low false discovery rate. Moreover, the GMJMCMC approach is adapted to make inference within the class of deep Bayesian regression models (which is a suggested in the package extension of various machine and statistical learning models like artificial neural networks, classification and regression trees, logic regressions and linear models). The reversible GMJMCMC, named RGMJMCMC, is also suggested. It makes transitions between the populations of variables in a way that satisfies the detailed balance equation. Based on several examples, it is shown that the BGNLM approach can be efficient for both inference and prediction in various applications. In particular, two ground physical laws (planetary mass law and third Kepler’s law) can be recovered from the data with large power and low false discovery rate. Three classification examples are also studied, where the comparison to other popular machine and statistical learning approaches is performed.
- Full text of the paper introducing MJMCMC for Bayesian variable selection: arXiv
- Full text of the paper introducing GMJMCMC for inference on Bayesian logic regressions: arXiv
- Full text of the paper introducing BGNLM and GMJMCMC algorithms for BGNLM: arXiv
- Supplementaries to these papers are available on GitHub
- Presentations of the talks are available on GitHub
- Latest issues of the package are available on GitHub
- Some applications of the package are available on GitHub
- Install binary on Linux or Mac Os:
install.packages("https://github.com/aliaksah/EMJMCMC2016/blob/master/EMJMCMC_1.4.3_R_x86_64-pc-linux-gnu.tar.gz?raw=true", repos = NULL, type="source")
- Notice that some dependencies might be required. To install dependencies before installation of the package run (additionally, this will load the source code for the EMJMCMC2016 package without installing it, which might be of interest for Windows users):
source("https://raw.githubusercontent.com/aliaksah/EMJMCMC2016/master/R/the_mode_jumping_package4.r")
- If you have a parallel version of openBlas in your backend and you want to run parallel inference with EMJMCMC, make sure to use:
library(RhpcBLASctl)
blas_set_num_threads(1)
omp_set_num_threads(1)
- An expert one threaded call of (R)(G)MJMCMC is (see runemjmcmc for details):
runemjmcmc(formula = formula1,data = data.example,recalc_margin = 2^10,estimator =estimate.bas.lm,estimator.args = list(data = data.example,prior = 3, g = 96 ,n=96),save.beta = T,interact = T,relations = c("","sin","cos","sigmoid","tanh","atan","erf"),relations.prob =c(0.4,0.1,0.1,0.1,0.1,0.1,0.1),interact.param=list(allow_offsprings=2,mutation_rate = 100, max.tree.size = 200000, Nvars.max = 95,p.allow.replace=0.9,p.allow.tree=0.5,p.nor=0.3,p.and = 0.7),n.models = 50000,unique = T,max.cpu = 10,max.cpu.glob = 10,create.table = F,create.hash = T,pseudo.paral = F,burn.in = 100,print.freq = 100)
- An expert parallel call of (R)(G)MCMC with predictions is (see pinferunemjmcmc for details):
pinferunemjmcmc(n.cores =30, report.level = 0.8 , num.mod.best = NM,simplify = T, predict = T,test.data = as.data.frame(test),link.function = g, runemjmcmc.params =list(formula = formula1,data = data.example,gen.prob = c(1,1,1,1,0),estimator =estimate.bas.glm.cpen,estimator.args = list(data = data.example,prior = aic.prior(),family = binomial(),yid=31, logn = log(143),r=exp(-0.5)),recalc_margin = 95, save.beta = T,interact = T,relations = c("gauss","tanh","atan","sin"),relations.prob =c(0.1,0.1,0.1,0.1),interact.param=list(allow_offsprings=4,mutation_rate = 100,last.mutation=1000, max.tree.size = 6, Nvars.max = 20,p.allow.replace=0.5,p.allow.tree=0.4,p.nor=0.3,p.and = 0.9),n.models = 7000,unique =T,max.cpu = 4,max.cpu.glob = 4,create.table = F,create.hash = T,pseudo.paral = T,burn.in = 100,print.freq = 1000,advanced.param = list(max.N.glob=as.integer(10), min.N.glob=as.integer(5), max.N=as.integer(3), min.N=as.integer(1), printable = F)))
- A simple call of parallel inference on Bayesian logic regression is (see LogicRegr for details):
LogicRegr(formula = formula1,data = data.example,family = "Gaussian",prior = "G",report.level = 0.5,d = 15,cmax = 2,kmax = 15,p.and = 0.9,p.not = 0.01,p.surv = 0.2,ncores = 32)
- Examples of simple calls of LogicRegr can be found on GitHub. Similar simple calls for BGNLM will be added soon.
Additionally the research was presented via the following selected contributions:
Academic journal articles
-
Hubin, Aliaksandr; Storvik, Geir Olve. Mode jumping MCMC for Bayesian variable selection in GLMM. Computational Statistics & Data Analysis (ISSN 0167-9473). 127 pp 281-297. doi: 10.1016/j.csda.2018.05.020. 2018.
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. A Novel Algorithmic Approach to Bayesian Logic Regression. Bayesian Analysis (ISSN 1936-0975). 2018.
-
Hubin, Aliaksandr, Storvik, Geir, Paul, & Butenko, Melinka (2020). A Bayesian Binomial Regression Model with Latent Gaussian Processes for Modelling DNA Methylation. Austrian Journal of Statistics, 49(4), 46-56.
Academic lectures
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. A novel algorithmic approach to Bayesian Logic Regression. Seminar, Tuesday Seminar at UiO; Blindern, 25.04.2017.
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. Deep Bayesian regression models. Seminar, Machine learning seminar at UiO; Oslo, 13.12.2018.
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. Deep Bayesian regression models. Invited lecture, Seminar on Bayesian Methods in Machine Learning; Yandex School of Data Analysis, Moscow, 16.03.2018.
Scientific lectures
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. Deep non-linear regression models in a Bayesian framework. Seminar, Biometrischen Kolloquium; Vienna, 16.10.2017.
-
Hubin, Aliaksandr; Storvik, Geir Olve; Grini, Paul Eivind. Variable selection in binomial regression with latent Gaussian field models for analysis of epigenetic data. Konferanse, CEN-ISBS-2017; Vienna, 28.08.2017 - 01.09.2017.
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. A novel GMJMCMC algorithm for Bayesian Logic Regression models. Workshop, ML@UiO; Oslo, 01.06.2017.
2016
-
Hubin, Aliaksandr; Storvik, Geir Olve. On Mode Jumping in MCMC for Bayesian Variable Selection within GLMM. Konferanse, 11th International Conference COMPUTER DATA ANALYSIS & MODELING 2016 Theoretical & Applied Stochastics; Minsk, 06.09.2016 - 09.09.2016.
-
Hubin, Aliaksandr; Storvik, Geir Olve. VARIABLE SELECTION IN BINOMIAL REGRESSION WITH LATENT GAUSSIAN FIELD MODELS FOR ANALYSIS OF EPIGENETIC DATA. Konferanse, Game of Epigenomics Conference; Dubrovnik, 24.04.2016 - 28.04.2016.
-
Hubin, Aliaksandr; Storvik, Geir Olve. Variable selection in logistic regression with a latent Gaussian field models with an application in epigenomics. Gjesteforelesning, Guest Lecture; Vienna, 21.03.2016.
2015
-
Hubin, Aliaksandr; Storvik, Geir Olve. On model selection in Hidden Markov Models with covariates. Workshop, Klækken Workshop 2015; Klækken, 29.05.2015.
-
Hubin, Aliaksandr; Storvik, Geir Olve. Variable selection in binomial regression with a latent Gaussian field models for analysis of epigenetic data. Konferanse, CMStatistics 2015; London, 11.12.2015 - 14.12.2015.
-
Hubin, Aliaksandr; Storvik, Geir Olve. Variable selection in binomial regression with a latent Gaussian field models for analysis of epigenetic data. Årsmøte, Norbis Annual Meeting 2015; Rosendal, 27.10.2015 - 30.10.2015.
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. Deep Bayesian regression models. Konferanse, FocuStat Conference; Oslo, 21.05.2018 - 25.05.2018.
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. Deep Bayesian regression models. Konferanse, NORDSTAT2018 conference; Tartu, 26.06.2018 - 29.06.2018.
Posters at scientific conferences
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. A novel algorithmic approach to Bayesian Logic Regression. 2017 14th Graybill Conference on Statistical Genomics and Genetics; Fort Collins, 05.06.2017 - 07.06.2017.
-
Hubin, Aliaksandr; Storvik, Geir Olve. Efficient mode jumping MCMC for Bayesian variable selection and model averaging in GLMM. Geilo Winter School 2017; Geilo, 15.01.2017 - 20.01.2017.
2016
-
Hubin, Aliaksandr; Storvik, Geir Olve. Efficient mode jumping MCMC for Bayesian variable selection in GLM with random effects models. NordStat 2016; Copenhagen, 27.06.2016 - 30.06.2016.
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. Deep Bayesian regression models. IBC2018; Barcelona, 08.07.2018 - 13.07.2018.
Doctoral dissertation
- Hubin, Aliaksandr. Bayesian model configuration, selection and averaging in complex regression contexts. : Series of dissertations submitted to the Faculty of Mathematics and Natural Sciences, University of Oslo (ISSN 1501-7710). (2035). pp 215. 2018.

Developed by Aliaksandr Hubin, Geir Storvik and Florian Frommlet
aliaksah/EMJMCMC2016 documentation built on July 27, 2023, 5:48 a.m.
In this R package problems of Bayesian model selection and model averaging are addressed in various complex regression contexts. The approaches developed within the package are based on the idea of marginalizing out parameters from the likelihood. This allows to work on the marginal space of models, which simplifies the search algorithms significantly. For the generalized linear mixed models an efficient mode jumping Monte Carlo Markov chain (MJMCMC) algorithm is implemented. The approach performs very well on simulated and real data. Further, the algorithm is extended to work with logic regressions, where one has a feature space consisting of various complicated logical expressions, which makes enumeration of all features computationally and memory infeasible in most of the cases. The genetically modified MJMCMC (GMJMCMC) algorithm is suggested to tackle this issue. The algorithm combines the idea of keeping and updating the populations of highly predictive logical expressions combined with MJMCMC for the efficient exploration of the model space. Several simulation and real data studies show that logical expressions of high orders can be recovered with large power and low false discovery rate. Moreover, the GMJMCMC approach is adapted to make inference within the class of deep Bayesian regression models (which is a suggested in the package extension of various machine and statistical learning models like artificial neural networks, classification and regression trees, logic regressions and linear models). The reversible GMJMCMC, named RGMJMCMC, is also suggested. It makes transitions between the populations of variables in a way that satisfies the detailed balance equation. Based on several examples, it is shown that the BGNLM approach can be efficient for both inference and prediction in various applications. In particular, two ground physical laws (planetary mass law and third Kepler’s law) can be recovered from the data with large power and low false discovery rate. Three classification examples are also studied, where the comparison to other popular machine and statistical learning approaches is performed.
- Full text of the paper introducing MJMCMC for Bayesian variable selection: arXiv
- Full text of the paper introducing GMJMCMC for inference on Bayesian logic regressions: arXiv
- Full text of the paper introducing BGNLM and GMJMCMC algorithms for BGNLM: arXiv
- Supplementaries to these papers are available on GitHub
- Presentations of the talks are available on GitHub
- Latest issues of the package are available on GitHub
- Some applications of the package are available on GitHub
- Install binary on Linux or Mac Os:
install.packages("https://github.com/aliaksah/EMJMCMC2016/blob/master/EMJMCMC_1.4.3_R_x86_64-pc-linux-gnu.tar.gz?raw=true", repos = NULL, type="source")
- Notice that some dependencies might be required. To install dependencies before installation of the package run (additionally, this will load the source code for the EMJMCMC2016 package without installing it, which might be of interest for Windows users):
source("https://raw.githubusercontent.com/aliaksah/EMJMCMC2016/master/R/the_mode_jumping_package4.r")
- If you have a parallel version of openBlas in your backend and you want to run parallel inference with EMJMCMC, make sure to use:
library(RhpcBLASctl)
blas_set_num_threads(1)
omp_set_num_threads(1)
- An expert one threaded call of (R)(G)MJMCMC is (see runemjmcmc for details):
runemjmcmc(formula = formula1,data = data.example,recalc_margin = 2^10,estimator =estimate.bas.lm,estimator.args = list(data = data.example,prior = 3, g = 96 ,n=96),save.beta = T,interact = T,relations = c("","sin","cos","sigmoid","tanh","atan","erf"),relations.prob =c(0.4,0.1,0.1,0.1,0.1,0.1,0.1),interact.param=list(allow_offsprings=2,mutation_rate = 100, max.tree.size = 200000, Nvars.max = 95,p.allow.replace=0.9,p.allow.tree=0.5,p.nor=0.3,p.and = 0.7),n.models = 50000,unique = T,max.cpu = 10,max.cpu.glob = 10,create.table = F,create.hash = T,pseudo.paral = F,burn.in = 100,print.freq = 100)
- An expert parallel call of (R)(G)MCMC with predictions is (see pinferunemjmcmc for details):
pinferunemjmcmc(n.cores =30, report.level = 0.8 , num.mod.best = NM,simplify = T, predict = T,test.data = as.data.frame(test),link.function = g, runemjmcmc.params =list(formula = formula1,data = data.example,gen.prob = c(1,1,1,1,0),estimator =estimate.bas.glm.cpen,estimator.args = list(data = data.example,prior = aic.prior(),family = binomial(),yid=31, logn = log(143),r=exp(-0.5)),recalc_margin = 95, save.beta = T,interact = T,relations = c("gauss","tanh","atan","sin"),relations.prob =c(0.1,0.1,0.1,0.1),interact.param=list(allow_offsprings=4,mutation_rate = 100,last.mutation=1000, max.tree.size = 6, Nvars.max = 20,p.allow.replace=0.5,p.allow.tree=0.4,p.nor=0.3,p.and = 0.9),n.models = 7000,unique =T,max.cpu = 4,max.cpu.glob = 4,create.table = F,create.hash = T,pseudo.paral = T,burn.in = 100,print.freq = 1000,advanced.param = list(max.N.glob=as.integer(10), min.N.glob=as.integer(5), max.N=as.integer(3), min.N=as.integer(1), printable = F)))
- A simple call of parallel inference on Bayesian logic regression is (see LogicRegr for details):
LogicRegr(formula = formula1,data = data.example,family = "Gaussian",prior = "G",report.level = 0.5,d = 15,cmax = 2,kmax = 15,p.and = 0.9,p.not = 0.01,p.surv = 0.2,ncores = 32)
- Examples of simple calls of LogicRegr can be found on GitHub. Similar simple calls for BGNLM will be added soon.
Additionally the research was presented via the following selected contributions:
Academic journal articles
-
Hubin, Aliaksandr; Storvik, Geir Olve. Mode jumping MCMC for Bayesian variable selection in GLMM. Computational Statistics & Data Analysis (ISSN 0167-9473). 127 pp 281-297. doi: 10.1016/j.csda.2018.05.020. 2018.
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. A Novel Algorithmic Approach to Bayesian Logic Regression. Bayesian Analysis (ISSN 1936-0975). 2018.
-
Hubin, Aliaksandr, Storvik, Geir, Paul, & Butenko, Melinka (2020). A Bayesian Binomial Regression Model with Latent Gaussian Processes for Modelling DNA Methylation. Austrian Journal of Statistics, 49(4), 46-56.
Academic lectures
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. A novel algorithmic approach to Bayesian Logic Regression. Seminar, Tuesday Seminar at UiO; Blindern, 25.04.2017.
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. Deep Bayesian regression models. Seminar, Machine learning seminar at UiO; Oslo, 13.12.2018.
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. Deep Bayesian regression models. Invited lecture, Seminar on Bayesian Methods in Machine Learning; Yandex School of Data Analysis, Moscow, 16.03.2018.
Scientific lectures
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. Deep non-linear regression models in a Bayesian framework. Seminar, Biometrischen Kolloquium; Vienna, 16.10.2017.
-
Hubin, Aliaksandr; Storvik, Geir Olve; Grini, Paul Eivind. Variable selection in binomial regression with latent Gaussian field models for analysis of epigenetic data. Konferanse, CEN-ISBS-2017; Vienna, 28.08.2017 - 01.09.2017.
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. A novel GMJMCMC algorithm for Bayesian Logic Regression models. Workshop, ML@UiO; Oslo, 01.06.2017. 2016
-
Hubin, Aliaksandr; Storvik, Geir Olve. On Mode Jumping in MCMC for Bayesian Variable Selection within GLMM. Konferanse, 11th International Conference COMPUTER DATA ANALYSIS & MODELING 2016 Theoretical & Applied Stochastics; Minsk, 06.09.2016 - 09.09.2016.
-
Hubin, Aliaksandr; Storvik, Geir Olve. VARIABLE SELECTION IN BINOMIAL REGRESSION WITH LATENT GAUSSIAN FIELD MODELS FOR ANALYSIS OF EPIGENETIC DATA. Konferanse, Game of Epigenomics Conference; Dubrovnik, 24.04.2016 - 28.04.2016.
-
Hubin, Aliaksandr; Storvik, Geir Olve. Variable selection in logistic regression with a latent Gaussian field models with an application in epigenomics. Gjesteforelesning, Guest Lecture; Vienna, 21.03.2016. 2015
-
Hubin, Aliaksandr; Storvik, Geir Olve. On model selection in Hidden Markov Models with covariates. Workshop, Klækken Workshop 2015; Klækken, 29.05.2015.
-
Hubin, Aliaksandr; Storvik, Geir Olve. Variable selection in binomial regression with a latent Gaussian field models for analysis of epigenetic data. Konferanse, CMStatistics 2015; London, 11.12.2015 - 14.12.2015.
-
Hubin, Aliaksandr; Storvik, Geir Olve. Variable selection in binomial regression with a latent Gaussian field models for analysis of epigenetic data. Årsmøte, Norbis Annual Meeting 2015; Rosendal, 27.10.2015 - 30.10.2015.
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. Deep Bayesian regression models. Konferanse, FocuStat Conference; Oslo, 21.05.2018 - 25.05.2018.
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. Deep Bayesian regression models. Konferanse, NORDSTAT2018 conference; Tartu, 26.06.2018 - 29.06.2018.
Posters at scientific conferences
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. A novel algorithmic approach to Bayesian Logic Regression. 2017 14th Graybill Conference on Statistical Genomics and Genetics; Fort Collins, 05.06.2017 - 07.06.2017.
-
Hubin, Aliaksandr; Storvik, Geir Olve. Efficient mode jumping MCMC for Bayesian variable selection and model averaging in GLMM. Geilo Winter School 2017; Geilo, 15.01.2017 - 20.01.2017. 2016
-
Hubin, Aliaksandr; Storvik, Geir Olve. Efficient mode jumping MCMC for Bayesian variable selection in GLM with random effects models. NordStat 2016; Copenhagen, 27.06.2016 - 30.06.2016.
-
Hubin, Aliaksandr; Storvik, Geir Olve; Frommlet, Florian. Deep Bayesian regression models. IBC2018; Barcelona, 08.07.2018 - 13.07.2018.
Doctoral dissertation
- Hubin, Aliaksandr. Bayesian model configuration, selection and averaging in complex regression contexts. : Series of dissertations submitted to the Faculty of Mathematics and Natural Sciences, University of Oslo (ISSN 1501-7710). (2035). pp 215. 2018.


Developed by Aliaksandr Hubin, Geir Storvik and Florian Frommlet
Add the following code to your website.
For more information on customizing the embed code, read Embedding Snippets.
