README.md
In jcduda/td2pLL: Fitting a time-dose two-parameter log-logistic model to time-dose-response data
Time-Dose Two-parameter Log-Logistic Model (td2pLL)
The goal of td2pLL is to fit and display time-dose two-parameter
log-logistic (td2pLL) models to appropriate data, e.g. cytotoxicity data
and to calculate D-optimal designs for experimental planning. The td2pLL
model is defined as

with

Installation
# install.packages("devtools")
devtools::install_github("jcduda/td2pLL", build_vignettes = TRUE)
Example 1: Plot a td2pLL model fit
library(td2pLL)
library(dplyr)
#> Warning: Paket 'dplyr' wurde unter R Version 4.1.3 erstellt
#>
#> Attache Paket: 'dplyr'
#> Die folgenden Objekte sind maskiert von 'package:stats':
#>
#> filter, lag
#> Die folgenden Objekte sind maskiert von 'package:base':
#>
#> intersect, setdiff, setequal, union
data(cytotox)
# Use subset of compound ASP
data_subset <- cytotox[cytotox$compound == "ASP", c("expo", "dose", "resp")]
colnames(data_subset)[1] <- "time"
fit <- fit_td2pLL(data = data_subset)
# In your Viewer in R Studio, you will see this when uncommenting the following line
# plot(fit)
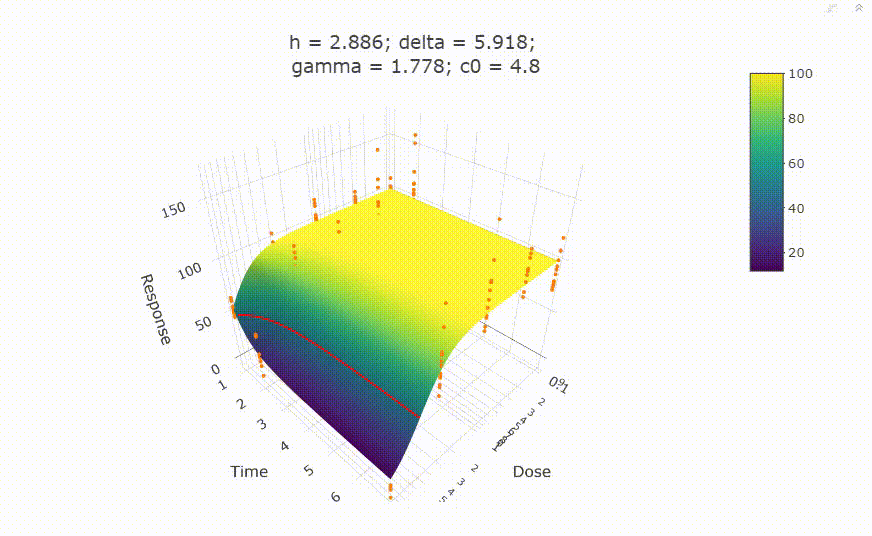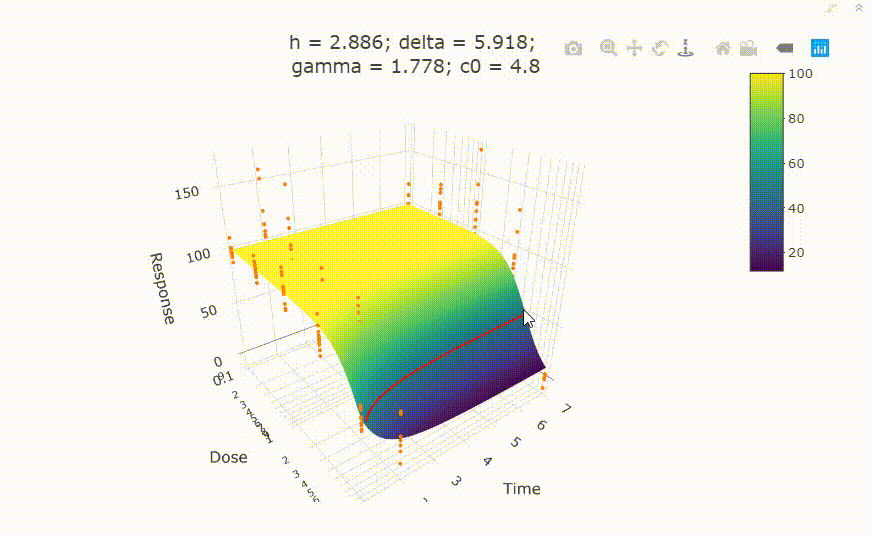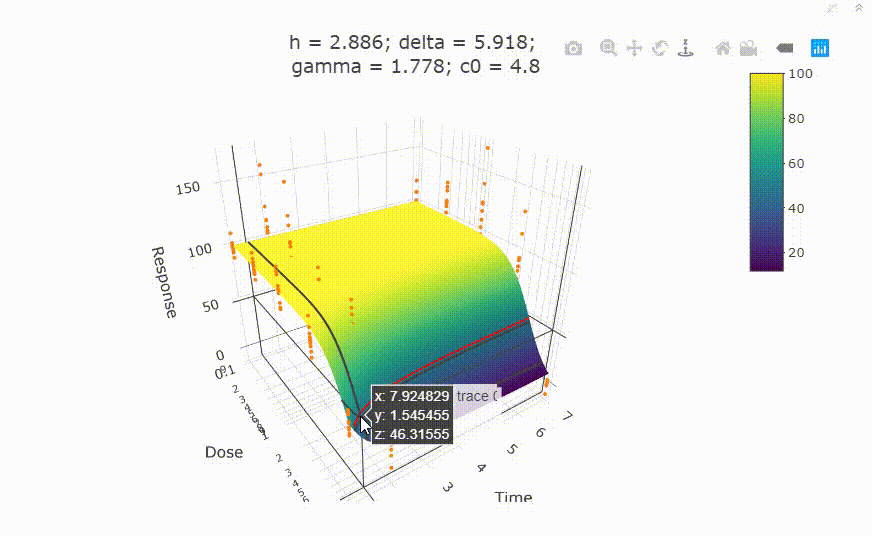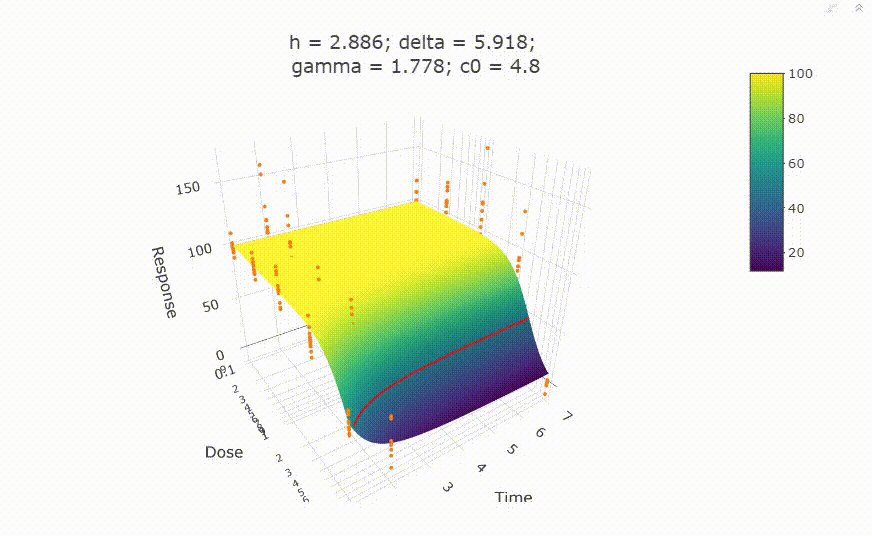
# change scale of dose axis to linear scale, so that dose=0 can be displayed:
# plot(fit, xaxis_scale = "linear")
# uncommenting the above line will show you the following in the Viewer or R Studio
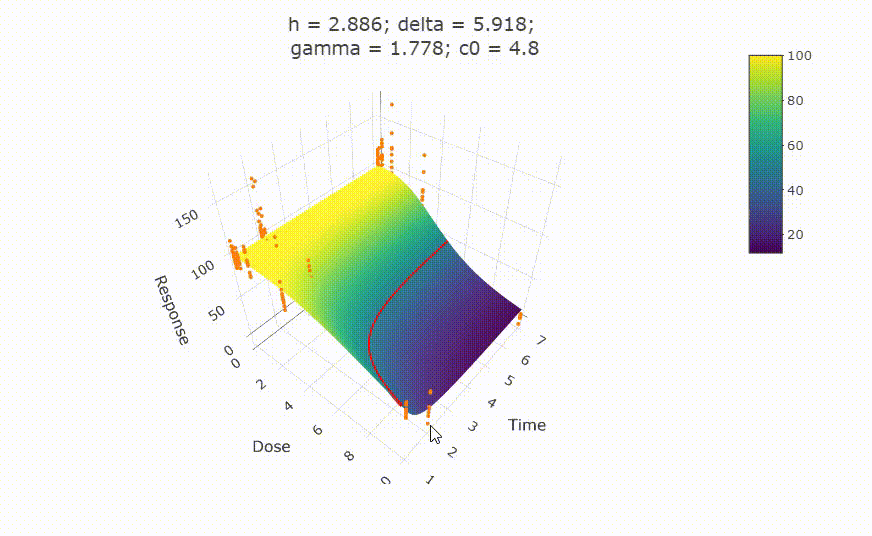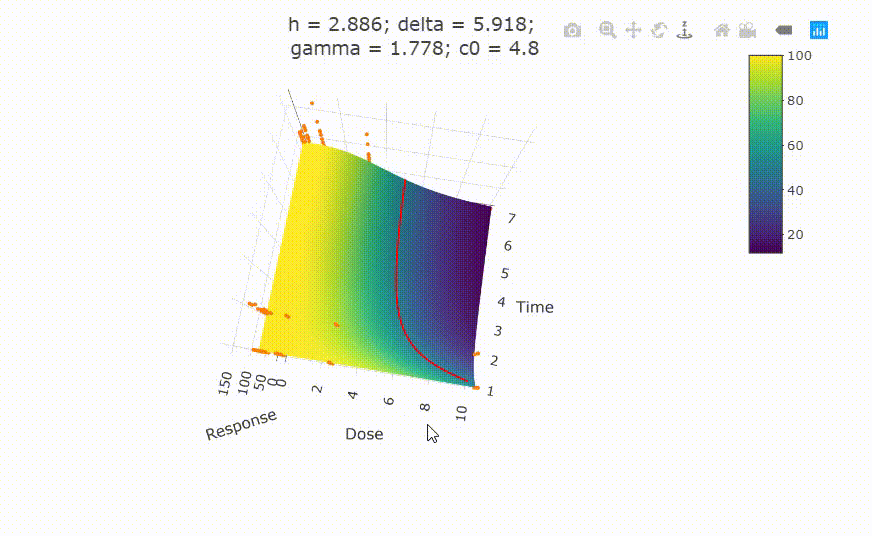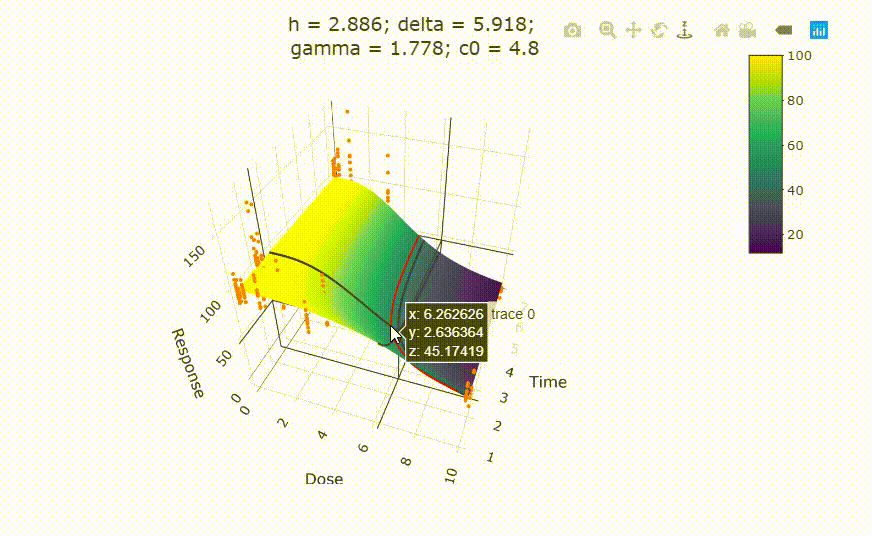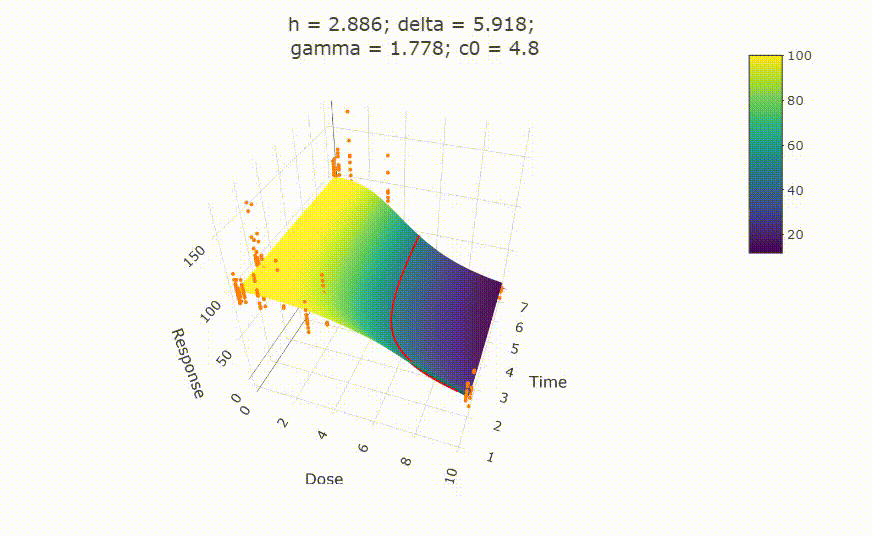
# Details on fit:
summary(fit)
#>
#> Formula: resp_m ~ 100 - 100 * (dose^h)/((delta * time^(-gamma) + c0)^h +
#> dose^h)
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> h 2.8878 0.7206 4.007 0.00130 **
#> delta 5.9221 1.9319 3.065 0.00839 **
#> gamma 1.7714 1.5939 1.111 0.28513
#> c0 4.7963 1.3508 3.551 0.00320 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 35.86 on 14 degrees of freedom
#>
#> Number of iterations to convergence: 11
#> Achieved convergence tolerance: 1.49e-08
# Calculate ED50 values at different (exposure) times:
get_ED50s(coefs = coef(fit), times = c(1, 2, 3))
#> time ED50
#> 1 1 10.718380
#> 2 2 6.531001
#> 3 3 5.642143
Example 2: Use two-step pipeline for conditional time-dose modeling
If you are not sure if you need to model time-dependency, you can use
the two-step anova-based pipeline using TDR(). In an initial step, via
nested anova it is checked if the time has an influence. Specifically, a
2pLL model with upper and lower limit set to 100 and 0, respectively,
that ignores the epxosure time component is the null model. The full
model is a 2pLL model where for each exposure time, a different
 parameter is fitted. Only the
parameter is fitted. Only the
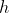 parameter is shared across exposure times. If the anova test between
these nested models is significant, an effect of the exposure time is
assumed to be true. In thas case, a td2pLL model is fitted in the second
step, the modeling step. If the pre-test does not yield a significant
result, then the regualr 2pLL model with upper and lower limit 100 and
0, respectively, is fitted.
parameter is shared across exposure times. If the anova test between
these nested models is significant, an effect of the exposure time is
assumed to be true. In thas case, a td2pLL model is fitted in the second
step, the modeling step. If the pre-test does not yield a significant
result, then the regualr 2pLL model with upper and lower limit 100 and
0, respectively, is fitted.
For the data of the above chosen compound, ASP, an influence of the
exposure time on the viability was detected.
TDR_res <- TDR(data = data_subset)
TDR_res
#> $pretest
#> $pretest$signif
#> [1] TRUE
#>
#> $pretest$alpha
#> [1] 0.05
#>
#> $pretest$anova
#> ANOVA table
#>
#> ModelDf RSS Df F value p value
#> 1st model 248 86851
#> 2nd model 246 72544 2 24.258 0.000
#>
#> $pretest$conv
#> [1] TRUE
#>
#>
#> $fit
#> Nonlinear regression model
#> model: resp_m ~ 100 - 100 * (dose^h)/((delta * time^(-gamma) + c0)^h + dose^h)
#> data: data_w
#> h delta gamma c0
#> 2.888 5.922 1.771 4.796
#> weighted residual sum-of-squares: 18004
#>
#> Number of iterations to convergence: 11
#> Achieved convergence tolerance: 1.49e-08
# Uncomment to see in Viewer
#plot(TDR_res$fit)
If we instead look at the measurements for the BOS compound and reduce
the data set a bit to a more realistic size, the pre-test suggests to
NOT model the time-dependency. Therefore, only a one-dimensionl 2pLL
model is fitted.
Note that if the data set is large enough, the anova pre-test will
always propose to model the time-effect as it will always find a
significant (but possibly irrelevant) difference in
 values between exposure periods.
values between exposure periods.
This significance-vs-relevance problem is always present in classical
frequentist statistical hypothesis testing.
data_subset <- cytotox[cytotox$compound == "BOS" &
cytotox$dose %in% c(0, 0.1, 0.316, 1),
c("expo", "dose", "resp")]
data_subset <- data_subset %>% group_by(expo, dose) %>%
dplyr::filter(dplyr::row_number() <= 3)
colnames(data_subset)[1] <- "time"
TDR_res <- TDR(data = data_subset)
TDR_res$pretest
#> $signif
#> [1] FALSE
#>
#> $alpha
#> [1] 0.05
#>
#> $anova
#> ANOVA table
#>
#> ModelDf RSS Df F value p value
#> 1st model 31 5098.4
#> 2nd model 29 4555.7 2 1.7273 0.1955
#>
#> $conv
#> [1] TRUE
plot(TDR_res$fit, type = "all")

Example 3: D-optimal design
Optimal design theory is highly developed and also well established in
pharmaceutical dose-finding studies.
For a D-optimal design of a td2pLL models, we no longer assume the
response-mean at control to be known(
 =100).
This has the effect that the optimal design proposes to have experiments
at the control (dose=0), which cannot be dismissed in practical
application.
=100).
This has the effect that the optimal design proposes to have experiments
at the control (dose=0), which cannot be dismissed in practical
application.
One can choose, however if the response-level for infitiely large doses
should be assumed to be known
(e.g.  for response=0 for large doses).
for response=0 for large doses).
If it is assumed to be known, the resulting optimal design will not
propose to measure at these high doses, as the response is assumed known
there and measurements at these high doses would not help to gain
further knowledge about the dose-time-response relationship.
The numerical back-bone is the Imperialist Competitive Algorithm (ICA)
by Masoudi et al. (2017).
It will take a few minutes to be calculated. Change to plot_cost=TRUE
to follow the optimization process.
td_opt_1 <- td_opt(param = c(h = 2, delta = 0.2, gamma = 1.3, c0 = 0.2),
Emax_known = TRUE,
# lower limit for time and dose
lx = c(1, exp(-8)),
# upper limit for time and dose
ux = c(10, 1),
# Choose trace=TRUE to follow the optimization process
ICA.control = list(ncount = 200, rseed = 1905, trace = FALSE,
plot_cost = FALSE),
iter = 400)
td_opt_1
#>
#> Finding locally optimal designs
#>
#> Call:
#> FIM defined directly via the argument 'fimfunc'
#>
#> iter x11 x12 x13 x14 x15 x16 x17
#> 1 1 4.138584 7.012220 2.308482 2.191634 9.622525 1.261818 2.437718
#> 45 45 9.708916 7.249875 1.001326 9.986133 6.656873 2.016469 2.771030
#> 89 89 9.923456 6.222053 1.000843 9.999907 7.961634 2.138536 2.212301
#> 134 134 9.997058 8.783593 1.000514 9.998855 7.364888 2.225970 2.133411
#> 178 178 9.999960 9.999906 7.173289 2.170807 2.197950 1.000012 1.000178
#> 222 222 9.999953 9.999596 7.001495 2.290375 2.200514 1.000033 1.000502
#> 267 267 9.999988 9.999990 6.487688 2.181538 2.220997 1.000002 1.000006
#> 311 311 9.999998 9.999983 6.482994 2.208655 2.226023 1.000001 1.000002
#> 355 355 9.999981 9.999984 6.490644 2.221738 2.216644 1.000001 1.000032
#> 400 400 9.999993 9.999971 6.197040 2.219562 2.224337 1.000001 1.000001
#> x21 x22 x23 x24 x25 x26
#> 1 0.04281632 0.4585485024 0.9081370497 0.1561994 0.2875296 0.4121813
#> 45 0.35368453 0.0061719561 0.3819896601 0.1374555 0.9852946 0.3334163
#> 89 0.32037638 0.0006030829 0.3986069542 0.1378312 0.9712651 0.4287708
#> 134 0.32150889 0.0003485619 0.3988487362 0.1377556 0.9717666 0.4116065
#> 178 0.13611805 0.3053410580 0.0003687687 0.1885288 0.4155264 0.3717006
#> 222 0.14710744 0.2946562852 0.0004140470 0.1881522 0.4154639 0.2965777
#> 267 0.14766975 0.2949168021 0.0003606696 0.1917453 0.4075099 0.2961824
#> 311 0.14615216 0.2969128030 0.0003358833 0.1917543 0.4016589 0.2951038
#> 355 0.14436923 0.2997571716 0.0003538701 0.1917005 0.3926499 0.2839684
#> 400 0.14485520 0.3007812155 0.0003402247 0.1916492 0.3919636 0.2818543
#> x27 w1 w2 w3 w4 w5 w6
#> 1 0.4901258 0.1242865 0.008285996 0.1766775 0.1200667 0.27706385 0.11275927
#> 45 0.1932682 0.2145677 0.142475930 0.2225141 0.1932950 0.01819131 0.09562984
#> 89 0.1649050 0.1493164 0.179821332 0.1859809 0.1715867 0.01039963 0.18235154
#> 134 0.1746463 0.1414627 0.189339726 0.1933476 0.1546359 0.00555770 0.16139973
#> 178 0.7059428 0.1369352 0.144814200 0.2113392 0.1483880 0.12958422 0.18124791
#> 222 0.6098555 0.1269629 0.125511960 0.2086322 0.1324518 0.11236451 0.16598775
#> 267 0.6086189 0.1306511 0.124139352 0.1983130 0.1425094 0.13352715 0.14376866
#> 311 0.6053688 0.1311783 0.132611160 0.1970448 0.1371726 0.13152605 0.14728062
#> 355 0.5801628 0.1300940 0.137447673 0.2012438 0.1344885 0.13147424 0.14029508
#> 400 0.5767679 0.1338137 0.134152946 0.1997585 0.1348531 0.13113991 0.13574009
#> w7 min_cost mean_cost
#> 1 0.18086020 -19.85208 -18.23572
#> 45 0.11332605 -21.85848 -21.64439
#> 89 0.12054353 -22.01560 -21.88176
#> 134 0.15425672 -22.06388 -21.96463
#> 178 0.04769122 -22.08616 -22.01238
#> 222 0.12808880 -22.09886 -22.04714
#> 267 0.12709140 -22.11651 -22.07441
#> 311 0.12318645 -22.11860 -22.08809
#> 355 0.12495679 -22.12097 -22.08951
#> 400 0.13054175 -22.12167 -22.09035
#>
#> Optimal designs (k=7):
#> Points1 Points2 Points3 Points4 Points5 Points6 Points7
#> /9.99999\ /9.99997\ /6.19704\ /2.21956\ /2.22434\ /1.00000\ /1.00000\
#> \0.14486/ \0.30078/ \0.00034/ \0.19165/ \0.39196/ \0.28185/ \0.57677/
#> Weights1 Weights2 Weights3 Weights4 Weights5 Weights6 Weights7
#> 0.134 0.134 0.200 0.135 0.131 0.136 0.131
#>
#> ICA iteration: 400
#> Criterion value: -22.12167
#> Total number of function evaluations: 115883
#> Total number of successful local search moves: 33159
#> Total number of successful revolution moves: 576
#> Convergence: Maximum_Iteration
#> Total number of successful assimilation moves: 10293
#> CPU time: 91.68 seconds!
The final design contains 7 time-dose points, where one will be placed
at the smallest dose-value with weight 0.2. The smallest dose-level can
be interpreted as dose=0.
If desired, this point can be splitted along the time-axis. This means
that instead of having 20 % of observations at dose = 0 and time = 6.2,
one can euivalently choose
- 20/3 % at dose = 0 and time = 1
- 20/3 % at dose = 0 and time = 10 and
- 20/3 % at dose = 0 and time = 2.2.
plot_td_des(td_opt_1)

One can check if the design is indeed optimal with a sensitivity plot.
If the entire plot is approximately below 0 at all points in the design
space and approximately zero at the proposed design points, then the
design is D-optimal for the assumed paramter.
plot_td_dcrit_equ(td_opt_1,
# to rotate the plot
plot_phi = 30)

jcduda/td2pLL documentation built on May 14, 2022, 6:48 p.m.
Time-Dose Two-parameter Log-Logistic Model (td2pLL)
The goal of td2pLL is to fit and display time-dose two-parameter log-logistic (td2pLL) models to appropriate data, e.g. cytotoxicity data and to calculate D-optimal designs for experimental planning. The td2pLL model is defined as
with
Installation
# install.packages("devtools")
devtools::install_github("jcduda/td2pLL", build_vignettes = TRUE)
Example 1: Plot a td2pLL model fit
library(td2pLL)
library(dplyr)
#> Warning: Paket 'dplyr' wurde unter R Version 4.1.3 erstellt
#>
#> Attache Paket: 'dplyr'
#> Die folgenden Objekte sind maskiert von 'package:stats':
#>
#> filter, lag
#> Die folgenden Objekte sind maskiert von 'package:base':
#>
#> intersect, setdiff, setequal, union
data(cytotox)
# Use subset of compound ASP
data_subset <- cytotox[cytotox$compound == "ASP", c("expo", "dose", "resp")]
colnames(data_subset)[1] <- "time"
fit <- fit_td2pLL(data = data_subset)
# In your Viewer in R Studio, you will see this when uncommenting the following line
# plot(fit)

# change scale of dose axis to linear scale, so that dose=0 can be displayed:
# plot(fit, xaxis_scale = "linear")
# uncommenting the above line will show you the following in the Viewer or R Studio

# Details on fit:
summary(fit)
#>
#> Formula: resp_m ~ 100 - 100 * (dose^h)/((delta * time^(-gamma) + c0)^h +
#> dose^h)
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> h 2.8878 0.7206 4.007 0.00130 **
#> delta 5.9221 1.9319 3.065 0.00839 **
#> gamma 1.7714 1.5939 1.111 0.28513
#> c0 4.7963 1.3508 3.551 0.00320 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 35.86 on 14 degrees of freedom
#>
#> Number of iterations to convergence: 11
#> Achieved convergence tolerance: 1.49e-08
# Calculate ED50 values at different (exposure) times:
get_ED50s(coefs = coef(fit), times = c(1, 2, 3))
#> time ED50
#> 1 1 10.718380
#> 2 2 6.531001
#> 3 3 5.642143
Example 2: Use two-step pipeline for conditional time-dose modeling
If you are not sure if you need to model time-dependency, you can use
the two-step anova-based pipeline using TDR(). In an initial step, via
nested anova it is checked if the time has an influence. Specifically, a
2pLL model with upper and lower limit set to 100 and 0, respectively,
that ignores the epxosure time component is the null model. The full
model is a 2pLL model where for each exposure time, a different
parameter is fitted. Only the
parameter is shared across exposure times. If the anova test between
these nested models is significant, an effect of the exposure time is
assumed to be true. In thas case, a td2pLL model is fitted in the second
step, the modeling step. If the pre-test does not yield a significant
result, then the regualr 2pLL model with upper and lower limit 100 and
0, respectively, is fitted.
For the data of the above chosen compound, ASP, an influence of the exposure time on the viability was detected.
TDR_res <- TDR(data = data_subset)
TDR_res
#> $pretest
#> $pretest$signif
#> [1] TRUE
#>
#> $pretest$alpha
#> [1] 0.05
#>
#> $pretest$anova
#> ANOVA table
#>
#> ModelDf RSS Df F value p value
#> 1st model 248 86851
#> 2nd model 246 72544 2 24.258 0.000
#>
#> $pretest$conv
#> [1] TRUE
#>
#>
#> $fit
#> Nonlinear regression model
#> model: resp_m ~ 100 - 100 * (dose^h)/((delta * time^(-gamma) + c0)^h + dose^h)
#> data: data_w
#> h delta gamma c0
#> 2.888 5.922 1.771 4.796
#> weighted residual sum-of-squares: 18004
#>
#> Number of iterations to convergence: 11
#> Achieved convergence tolerance: 1.49e-08
# Uncomment to see in Viewer
#plot(TDR_res$fit)
If we instead look at the measurements for the BOS compound and reduce the data set a bit to a more realistic size, the pre-test suggests to NOT model the time-dependency. Therefore, only a one-dimensionl 2pLL model is fitted.
Note that if the data set is large enough, the anova pre-test will
always propose to model the time-effect as it will always find a
significant (but possibly irrelevant) difference in
values between exposure periods.
This significance-vs-relevance problem is always present in classical frequentist statistical hypothesis testing.
data_subset <- cytotox[cytotox$compound == "BOS" &
cytotox$dose %in% c(0, 0.1, 0.316, 1),
c("expo", "dose", "resp")]
data_subset <- data_subset %>% group_by(expo, dose) %>%
dplyr::filter(dplyr::row_number() <= 3)
colnames(data_subset)[1] <- "time"
TDR_res <- TDR(data = data_subset)
TDR_res$pretest
#> $signif
#> [1] FALSE
#>
#> $alpha
#> [1] 0.05
#>
#> $anova
#> ANOVA table
#>
#> ModelDf RSS Df F value p value
#> 1st model 31 5098.4
#> 2nd model 29 4555.7 2 1.7273 0.1955
#>
#> $conv
#> [1] TRUE
plot(TDR_res$fit, type = "all")

Example 3: D-optimal design
Optimal design theory is highly developed and also well established in pharmaceutical dose-finding studies.
For a D-optimal design of a td2pLL models, we no longer assume the
response-mean at control to be known(
=100).
This has the effect that the optimal design proposes to have experiments
at the control (dose=0), which cannot be dismissed in practical
application.
One can choose, however if the response-level for infitiely large doses
should be assumed to be known
(e.g.
for response=0 for large doses).
If it is assumed to be known, the resulting optimal design will not propose to measure at these high doses, as the response is assumed known there and measurements at these high doses would not help to gain further knowledge about the dose-time-response relationship.
The numerical back-bone is the Imperialist Competitive Algorithm (ICA) by Masoudi et al. (2017).
It will take a few minutes to be calculated. Change to plot_cost=TRUE
to follow the optimization process.
td_opt_1 <- td_opt(param = c(h = 2, delta = 0.2, gamma = 1.3, c0 = 0.2),
Emax_known = TRUE,
# lower limit for time and dose
lx = c(1, exp(-8)),
# upper limit for time and dose
ux = c(10, 1),
# Choose trace=TRUE to follow the optimization process
ICA.control = list(ncount = 200, rseed = 1905, trace = FALSE,
plot_cost = FALSE),
iter = 400)
td_opt_1
#>
#> Finding locally optimal designs
#>
#> Call:
#> FIM defined directly via the argument 'fimfunc'
#>
#> iter x11 x12 x13 x14 x15 x16 x17
#> 1 1 4.138584 7.012220 2.308482 2.191634 9.622525 1.261818 2.437718
#> 45 45 9.708916 7.249875 1.001326 9.986133 6.656873 2.016469 2.771030
#> 89 89 9.923456 6.222053 1.000843 9.999907 7.961634 2.138536 2.212301
#> 134 134 9.997058 8.783593 1.000514 9.998855 7.364888 2.225970 2.133411
#> 178 178 9.999960 9.999906 7.173289 2.170807 2.197950 1.000012 1.000178
#> 222 222 9.999953 9.999596 7.001495 2.290375 2.200514 1.000033 1.000502
#> 267 267 9.999988 9.999990 6.487688 2.181538 2.220997 1.000002 1.000006
#> 311 311 9.999998 9.999983 6.482994 2.208655 2.226023 1.000001 1.000002
#> 355 355 9.999981 9.999984 6.490644 2.221738 2.216644 1.000001 1.000032
#> 400 400 9.999993 9.999971 6.197040 2.219562 2.224337 1.000001 1.000001
#> x21 x22 x23 x24 x25 x26
#> 1 0.04281632 0.4585485024 0.9081370497 0.1561994 0.2875296 0.4121813
#> 45 0.35368453 0.0061719561 0.3819896601 0.1374555 0.9852946 0.3334163
#> 89 0.32037638 0.0006030829 0.3986069542 0.1378312 0.9712651 0.4287708
#> 134 0.32150889 0.0003485619 0.3988487362 0.1377556 0.9717666 0.4116065
#> 178 0.13611805 0.3053410580 0.0003687687 0.1885288 0.4155264 0.3717006
#> 222 0.14710744 0.2946562852 0.0004140470 0.1881522 0.4154639 0.2965777
#> 267 0.14766975 0.2949168021 0.0003606696 0.1917453 0.4075099 0.2961824
#> 311 0.14615216 0.2969128030 0.0003358833 0.1917543 0.4016589 0.2951038
#> 355 0.14436923 0.2997571716 0.0003538701 0.1917005 0.3926499 0.2839684
#> 400 0.14485520 0.3007812155 0.0003402247 0.1916492 0.3919636 0.2818543
#> x27 w1 w2 w3 w4 w5 w6
#> 1 0.4901258 0.1242865 0.008285996 0.1766775 0.1200667 0.27706385 0.11275927
#> 45 0.1932682 0.2145677 0.142475930 0.2225141 0.1932950 0.01819131 0.09562984
#> 89 0.1649050 0.1493164 0.179821332 0.1859809 0.1715867 0.01039963 0.18235154
#> 134 0.1746463 0.1414627 0.189339726 0.1933476 0.1546359 0.00555770 0.16139973
#> 178 0.7059428 0.1369352 0.144814200 0.2113392 0.1483880 0.12958422 0.18124791
#> 222 0.6098555 0.1269629 0.125511960 0.2086322 0.1324518 0.11236451 0.16598775
#> 267 0.6086189 0.1306511 0.124139352 0.1983130 0.1425094 0.13352715 0.14376866
#> 311 0.6053688 0.1311783 0.132611160 0.1970448 0.1371726 0.13152605 0.14728062
#> 355 0.5801628 0.1300940 0.137447673 0.2012438 0.1344885 0.13147424 0.14029508
#> 400 0.5767679 0.1338137 0.134152946 0.1997585 0.1348531 0.13113991 0.13574009
#> w7 min_cost mean_cost
#> 1 0.18086020 -19.85208 -18.23572
#> 45 0.11332605 -21.85848 -21.64439
#> 89 0.12054353 -22.01560 -21.88176
#> 134 0.15425672 -22.06388 -21.96463
#> 178 0.04769122 -22.08616 -22.01238
#> 222 0.12808880 -22.09886 -22.04714
#> 267 0.12709140 -22.11651 -22.07441
#> 311 0.12318645 -22.11860 -22.08809
#> 355 0.12495679 -22.12097 -22.08951
#> 400 0.13054175 -22.12167 -22.09035
#>
#> Optimal designs (k=7):
#> Points1 Points2 Points3 Points4 Points5 Points6 Points7
#> /9.99999\ /9.99997\ /6.19704\ /2.21956\ /2.22434\ /1.00000\ /1.00000\
#> \0.14486/ \0.30078/ \0.00034/ \0.19165/ \0.39196/ \0.28185/ \0.57677/
#> Weights1 Weights2 Weights3 Weights4 Weights5 Weights6 Weights7
#> 0.134 0.134 0.200 0.135 0.131 0.136 0.131
#>
#> ICA iteration: 400
#> Criterion value: -22.12167
#> Total number of function evaluations: 115883
#> Total number of successful local search moves: 33159
#> Total number of successful revolution moves: 576
#> Convergence: Maximum_Iteration
#> Total number of successful assimilation moves: 10293
#> CPU time: 91.68 seconds!
The final design contains 7 time-dose points, where one will be placed at the smallest dose-value with weight 0.2. The smallest dose-level can be interpreted as dose=0.
If desired, this point can be splitted along the time-axis. This means that instead of having 20 % of observations at dose = 0 and time = 6.2, one can euivalently choose
- 20/3 % at dose = 0 and time = 1
- 20/3 % at dose = 0 and time = 10 and
- 20/3 % at dose = 0 and time = 2.2.
plot_td_des(td_opt_1)

One can check if the design is indeed optimal with a sensitivity plot. If the entire plot is approximately below 0 at all points in the design space and approximately zero at the proposed design points, then the design is D-optimal for the assumed paramter.
plot_td_dcrit_equ(td_opt_1,
# to rotate the plot
plot_phi = 30)

Add the following code to your website.
For more information on customizing the embed code, read Embedding Snippets.
