README.md
In linxihui/sml: Machine Learning for Survival Data
Machine learning for survival data
Install
# Install sml
library(devtools);
install_github('linxihui/sml');
Background: Cox's proportional hazard model
Cox's model assumes that the proportional hazards are proportional among all observations. With such assumption,
a partial likelihood comes up, which can also be treated as a profile and conditional likelihood, which does not
involve a baseline hazard function, and thus parameters of interest gain more degree freedom to estimate.
The Cox partial likelihood looks like
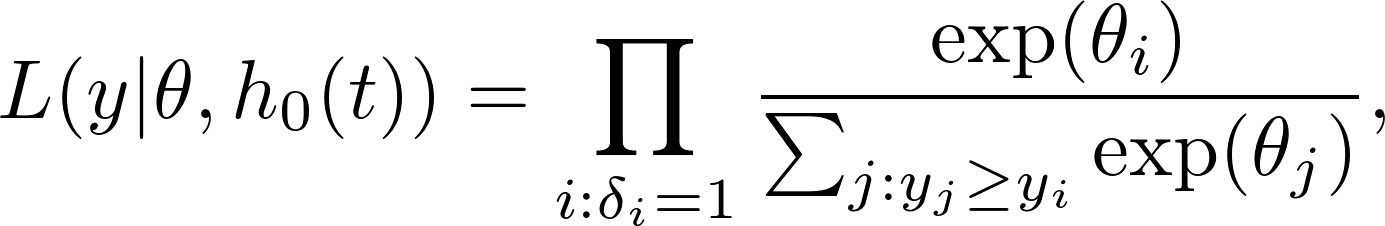
where $\theta_i$'s are usually called links, or log risk (as $\exp{\theta_i}$'s are called risk).
In Cox's model,
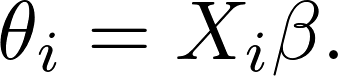
Currently implemented algorithms
Gaussian process
Gaussian process regression and classification have been shown to be powerful. However, no extension to survival
is available in R. However, the extension is quite straight forward, by assuming that $\theta$ are sampled from
a Gaussian process (prior), i.e.,
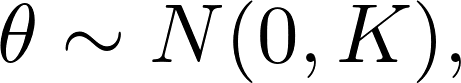
where $K = (k_{ij}) = K(x_i, x_j)$ is the kernel matrix.
The posterior distribution,
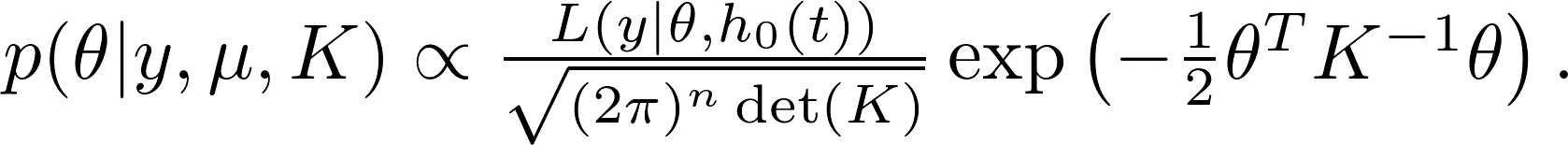
Define
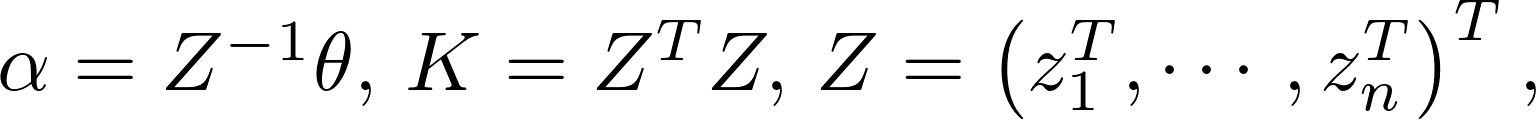
After taking the logarithm, we get
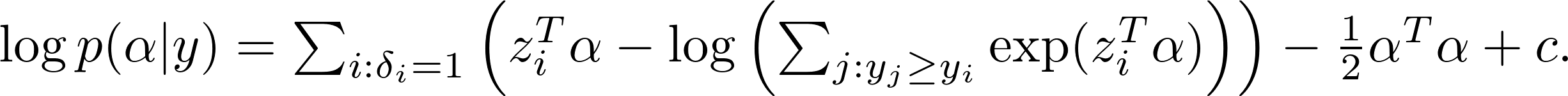
The max-a-posterior(MAP) estimate $\hat\alpha_{\text{\tiny MAP}}$ (and thus $\hat\theta_{\text{\tiny MAP}}$) can be estimated by ridge regression solver (such as glmnet). This is implemented as gpsrc.
# Survival Gaussian process regression
library(survival);
library(sml);
set.seed(123);
data(pbc, package = 'randomForestSRC');
pbc <- na.omit(pbc);
i.tr <- sample(nrow(pbc), 100);
gp <- gpsrc(Surv(days, status) ~., data = pbc[i.tr, ], kernel = 'laplacedot');
gp.pred <- predict(gp, pbc[-i.tr, ]);
gp.cInd <- survConcordance(Surv(days, status) ~ gp.pred, data = pbc[-i.tr, ]);
cat('C-index:', gp.cInd$concordance, '\n');
## C-index: 0.8492154
Extreme learning machine
Extreme learning machine (ELM) was first introduced as a quick method to train
a single hidden layer neural network. However, ELM is more related to SVM.
Indeed, neural network trained to learn the hidden features and SVM maps input
to high dimension feature space which is determinant. Instead, ELM randomly maps
input to high dimension feature space. This random feature mapping turns out to
work well.
Denote $m$ as number of hidden features, $z_1, \cdots, z_m$, where
$z_k = \sigma(x_i^T w_{ij})$, where $w_{ij}$ is randomly and independently
sampled and $\sigma$ is a chosen activating function. A Cox model, or a
ridge-regularized Cox model is then applied on the hidden features.
Usually, $m$ is chosen to be big, probably even bigger than the number of
sample $n$, like 500 or 1000 and ridge regulaization applied.
The question is, why random mapping even works? Since usually $m > p$ (input
dimension) and $w_{ij}$ are independently sampled, thus
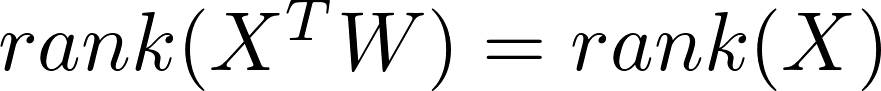
almost surely. However, after applying a non-linear activating function,
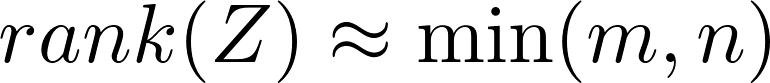
# Survival ELM
elm.f <- elm(Surv(days, status) ~., data = pbc[i.tr, ], nhid = 500);
elm.pred <- predict(object = elm.f, newdata = pbc[-i.tr, ], type = 'link');
elm.cInd <- survConcordance(Surv(days, status) ~ elm.pred, data = pbc[-i.tr, ]);
cat('C-index:', elm.cInd$concordance, '\n');
## C-index: 0.839515
Kernel-weighted K-Nearest-Neighbour Kaplan-Meier / Nelson-Aalen estimators
Let $K = (k_{ij}) = K(x_i, x_j)$ be the kernel matrix. The weighted Kaplan-Meier estimate for survival function is
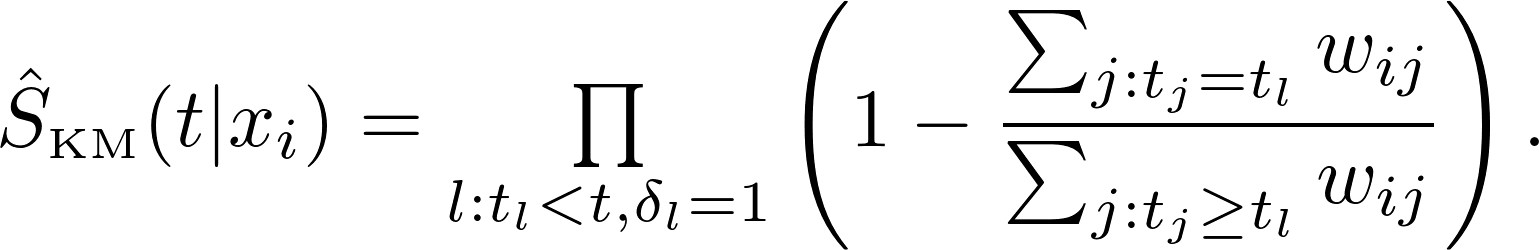
The weighted Nelson-Aalen estimator for the cummulative hazard function is
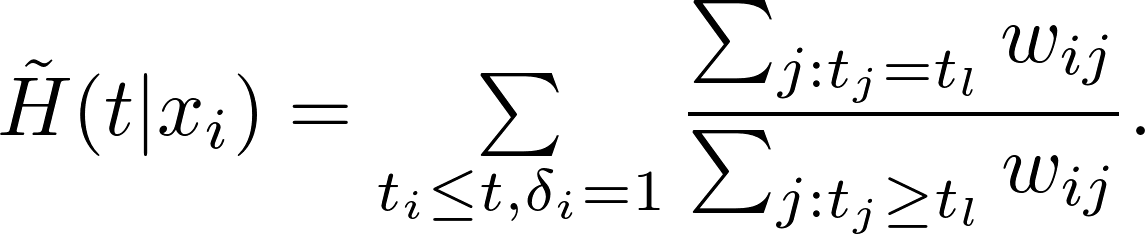
# Kernel-weighted KNN Kaplan-Meier
kkm.pred <- kkm(
Surv(days, status) ~., data = pbc[i.tr, ], xtest = pbc[-i.tr, ],
kernel = 'laplacedot', kpar = list(sigma = 0.1), k = 50
);
kkm.cInd <- survConcordance(
Surv(days, status) ~ I(1 - kkm.pred$test.predicted.survival[, 30]),
data = pbc[-i.tr, ]
);
cat('C-index:', kkm.cInd$concordance, '\n');
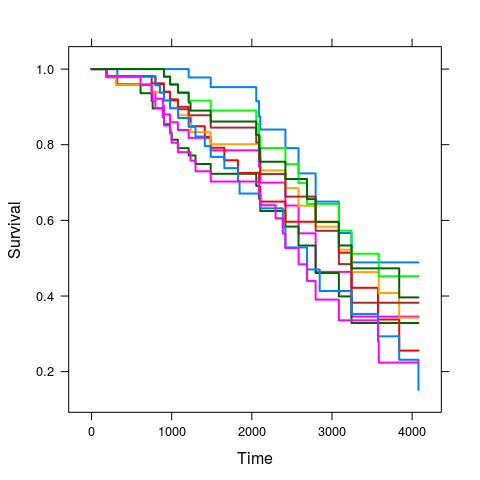
plot(kkm.pred, subset = sample(length(i.tr), 10), lwd = 2);
## C-index: 0.8446505
linxihui/sml documentation built on May 21, 2019, 6:39 a.m.
Machine learning for survival data
Install
# Install sml
library(devtools);
install_github('linxihui/sml');
Background: Cox's proportional hazard model
Cox's model assumes that the proportional hazards are proportional among all observations. With such assumption, a partial likelihood comes up, which can also be treated as a profile and conditional likelihood, which does not involve a baseline hazard function, and thus parameters of interest gain more degree freedom to estimate.
The Cox partial likelihood looks like
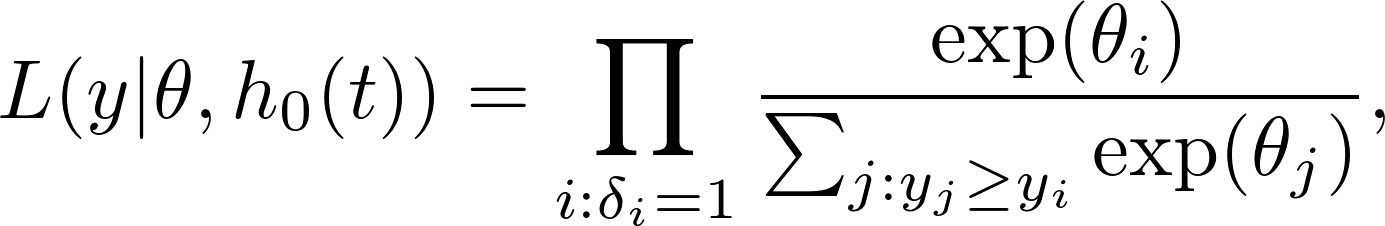
where $\theta_i$'s are usually called links, or log risk (as $\exp{\theta_i}$'s are called risk).
In Cox's model,
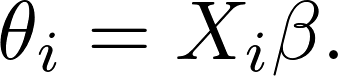
Currently implemented algorithms
Gaussian process
Gaussian process regression and classification have been shown to be powerful. However, no extension to survival is available in R. However, the extension is quite straight forward, by assuming that $\theta$ are sampled from a Gaussian process (prior), i.e.,
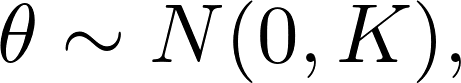
where $K = (k_{ij}) = K(x_i, x_j)$ is the kernel matrix.
The posterior distribution,
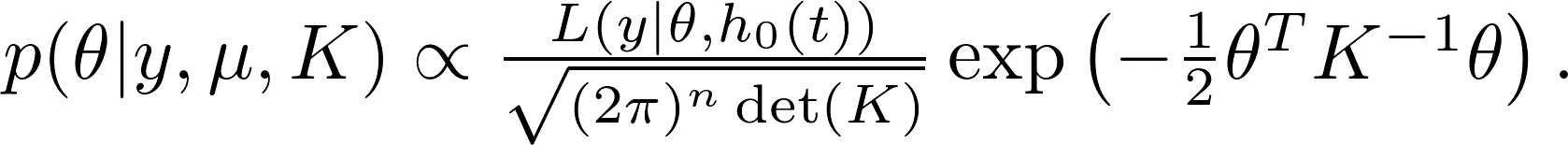
Define
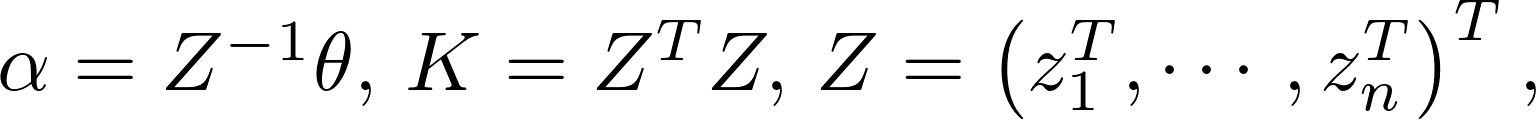
After taking the logarithm, we get
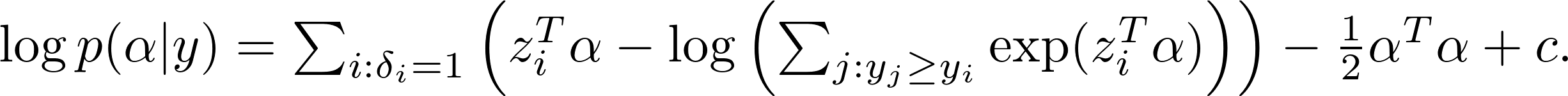
The max-a-posterior(MAP) estimate $\hat\alpha_{\text{\tiny MAP}}$ (and thus $\hat\theta_{\text{\tiny MAP}}$) can be estimated by ridge regression solver (such as glmnet). This is implemented as gpsrc.
# Survival Gaussian process regression
library(survival);
library(sml);
set.seed(123);
data(pbc, package = 'randomForestSRC');
pbc <- na.omit(pbc);
i.tr <- sample(nrow(pbc), 100);
gp <- gpsrc(Surv(days, status) ~., data = pbc[i.tr, ], kernel = 'laplacedot');
gp.pred <- predict(gp, pbc[-i.tr, ]);
gp.cInd <- survConcordance(Surv(days, status) ~ gp.pred, data = pbc[-i.tr, ]);
cat('C-index:', gp.cInd$concordance, '\n');
## C-index: 0.8492154
Extreme learning machine
Extreme learning machine (ELM) was first introduced as a quick method to train a single hidden layer neural network. However, ELM is more related to SVM. Indeed, neural network trained to learn the hidden features and SVM maps input to high dimension feature space which is determinant. Instead, ELM randomly maps input to high dimension feature space. This random feature mapping turns out to work well.
Denote $m$ as number of hidden features, $z_1, \cdots, z_m$, where $z_k = \sigma(x_i^T w_{ij})$, where $w_{ij}$ is randomly and independently sampled and $\sigma$ is a chosen activating function. A Cox model, or a ridge-regularized Cox model is then applied on the hidden features. Usually, $m$ is chosen to be big, probably even bigger than the number of sample $n$, like 500 or 1000 and ridge regulaization applied.
The question is, why random mapping even works? Since usually $m > p$ (input dimension) and $w_{ij}$ are independently sampled, thus
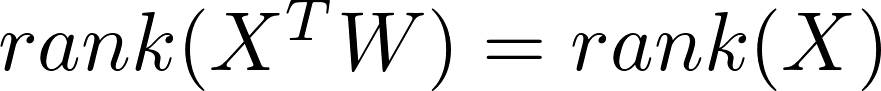
almost surely. However, after applying a non-linear activating function,
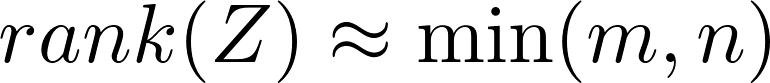
# Survival ELM
elm.f <- elm(Surv(days, status) ~., data = pbc[i.tr, ], nhid = 500);
elm.pred <- predict(object = elm.f, newdata = pbc[-i.tr, ], type = 'link');
elm.cInd <- survConcordance(Surv(days, status) ~ elm.pred, data = pbc[-i.tr, ]);
cat('C-index:', elm.cInd$concordance, '\n');
## C-index: 0.839515
Kernel-weighted K-Nearest-Neighbour Kaplan-Meier / Nelson-Aalen estimators
Let $K = (k_{ij}) = K(x_i, x_j)$ be the kernel matrix. The weighted Kaplan-Meier estimate for survival function is
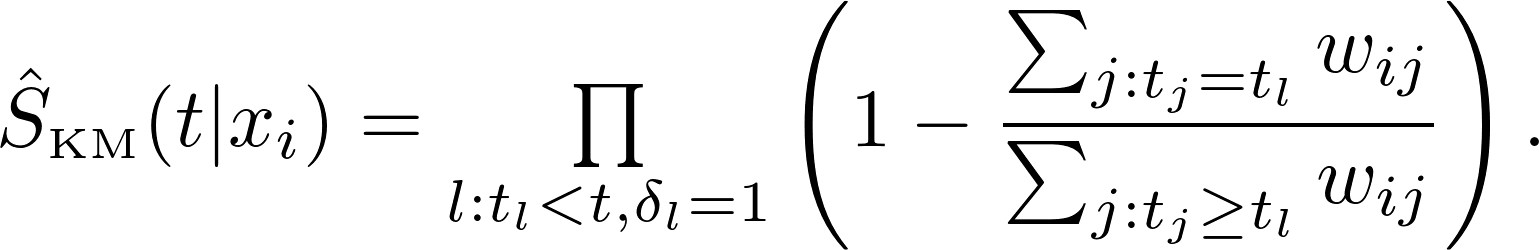
The weighted Nelson-Aalen estimator for the cummulative hazard function is
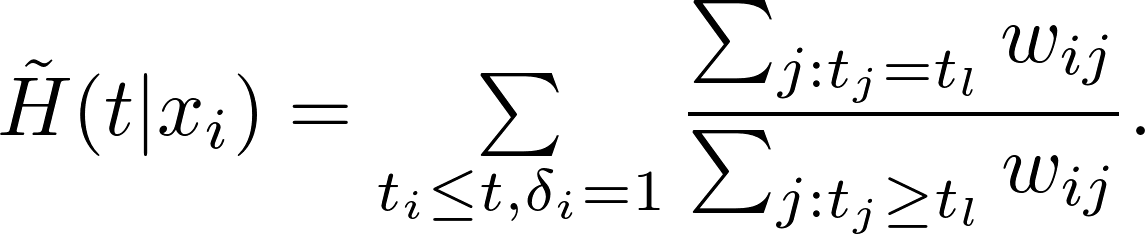
# Kernel-weighted KNN Kaplan-Meier
kkm.pred <- kkm(
Surv(days, status) ~., data = pbc[i.tr, ], xtest = pbc[-i.tr, ],
kernel = 'laplacedot', kpar = list(sigma = 0.1), k = 50
);
kkm.cInd <- survConcordance(
Surv(days, status) ~ I(1 - kkm.pred$test.predicted.survival[, 30]),
data = pbc[-i.tr, ]
);
cat('C-index:', kkm.cInd$concordance, '\n');
plot(kkm.pred, subset = sample(length(i.tr), 10), lwd = 2);
## C-index: 0.8446505

Add the following code to your website.
For more information on customizing the embed code, read Embedding Snippets.
