README.md
In adamwbolton/rattitude: Attitude Estimation
rattitude
rattitude has two main functions: (1) inertial-based three-axis
accelerometer calibration and (2) attitude determination.
Installation
# install.packages("devtools")
devtools::install_github("adamwbolton/rattitude")
Example
library(rattitude)
Rotations
Rotations can be specified either as rotation matrices, sequences of
Euler angles, or rotation quaternions. One can convert between the three
with the following functions: euler_to_rotation,
euler_to_quaternion, rotation_to_quaternion, rotation_to_euler,
quaternion_to_euler, quaternion_to_rotation. Let’s start with a
rotation of 90 degrees about the x-axis and convert this to a rotation
matrix:
# toy data
pitch <- 90
roll <- 0
yaw <- 0
R <- euler_to_rotation(pitch, roll,yaw, units = "degrees")
# rotation matrix
R
#> [,1] [,2] [,3]
#> [1,] 1 0.000000e+00 0.000000e+00
#> [2,] 0 6.123234e-17 -1.000000e+00
#> [3,] 0 1.000000e+00 6.123234e-17
converting this back to Euler angles
# convert back to euler angles
rotation_to_euler(R)
#> $pitch
#> [1] 90
#>
#> $roll
#> [1] 0
#>
#> $yaw
#> [1] 0
and then to a rotation quaternion
# rotation to quaternion
q <- rotation_to_quaterion(R)
q
#> [1] 0.7071068 0.0000000 0.0000000 0.7071068
and back to Euler angles
quaterion_to_euler(q)
#> $pitch
#> [1] 90
#>
#> $roll
#> [1] 0
#>
#> $yaw
#> [1] 0
Calibration
The calibration for the inertial-based three-axis accelerometers is done
through the following first-order model:
where 
.
For the x-axis accelerometer,
is the bias,
is the sensitivity,
is the coefficient for the cross-axis sensitivity of
,
is the coefficient for the cross-axis sensitivity of
. The sensitivity matrix,
, and the bias vector,
, are given by
Calibration is done through the calibration function which takes
matrices
and
are arguments and returns the estimates of the
sensitivity and bias terms of the model above. Each row of
should have unit norm.
# create sensitivity matrix and bias vector
Beta0 <- c(0,0,0)
Beta <- diag(3) + matrix(rnorm(9,sd = 1e-4),nrow = 3)
# number of observations
n <- 10
# create matrix of gravity vectors
G <- matrix(rnorm(3*n), nrow =n)
G <- t(apply(G,1,FUN = function(x) x/norm(x,"2")))
# simulate responses based on calibration model with some noise
V <- G %*% Beta + Beta0 + matrix(rnorm(3*n, sd = 1e-2), nrow =n)
To fit the calibration model….
cal <- calibration(V,G)
Estimates of the sensitivity and bias terms in the model
cal$coef
#> $BetaHat
#> [,1] [,2] [,3]
#> [1,] 0.999601350 -0.016203819 0.002389500
#> [2,] 0.002422397 0.991612219 0.004893546
#> [3,] 0.005512963 0.007760368 1.002375200
#>
#> $Beta
#> [,1] [,2] [,3]
#> [1,] 1.000076e+00 8.059277e-05 1.135893e-04
#> [2,] 5.456315e-05 9.997552e-01 4.076539e-06
#> [3,] -1.038208e-04 -6.119115e-06 9.999143e-01
Estimates of the gravity vectors given by 
cal$Ghat
#> [,1] [,2] [,3]
#> [1,] -0.708042358 0.59581656 0.38242550
#> [2,] -0.115753373 0.96577065 0.18156004
#> [3,] 0.049395167 -1.02113780 -0.01229979
#> [4,] 0.122635690 0.05509749 -0.98369083
#> [5,] -0.003190392 0.70095190 0.71947303
#> [6,] -0.859939419 0.30872718 0.44181834
#> [7,] -0.256087371 -0.94040855 0.18621783
#> [8,] -0.927600534 -0.15038225 -0.28208025
#> [9,] 0.130101505 -0.64665419 0.74144121
#> [10,] 0.971819066 0.27117651 0.07182864
Estimate of
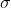from calibration model
cal$sd
#> [1] 0.01080902
Attitude Estimation
Wahba’s problem seeks to minimize the cost-function
where
is the u-th 3-vector measurement in the reference
frame,
is the corresponding i-th 3-vector measurement in the
body frame
is a 
rotation matrix between the reference frame and body
frame. The optimal rotation,
can be found using Davenport’s q-method:
Define the corresponding gain function:
\begin{align}
G(R) & = 1- L(R) \\ & = \sum_{i=1}^n tr(\mathbf{w}_i^T \mathbf{R} \mathbf{v}_i) \\ & =
tr(\mathbf{W}^T \mathbf{R} \mathbf{V}) \\ & =
tr(\mathbf{R} \mathbf{B}^T)
\end{align}
where 
Parameterizing the rotation matrix in terms of quaternion, 
we have
![ \mathbf{R}(q) = (q_r - \| \mathbf{q}_v \|^2) \mathbf{I}_3
+ 2 \mathbf{q}_v \mathbf{q}_v^T - 2 q_r
[\mathbf{q}_v]_x ](https://latex.codecogs.com/png.image?%5Cdpi%7B110%7D&space;%5Cbg_white&space;%0A%5Cmathbf%7BR%7D%28q%29%20%3D%20%28q_r%20-%20%5C%7C%20%5Cmathbf%7Bq%7D_v%20%5C%7C%5E2%29%20%5Cmathbf%7BI%7D_3%20%2B%202%20%5Cmathbf%7Bq%7D_v%20%5Cmathbf%7Bq%7D_v%5ET%20-%202%20q_r%20%5B%5Cmathbf%7Bq%7D_v%5D_x%0A)
where
![[\mathbf{q}_v]_x](https://latex.codecogs.com/png.image?%5Cdpi%7B110%7D&space;%5Cbg_white&space;%5B%5Cmathbf%7Bq%7D_v%5D_x)
is the skew-symmetric matrix of vector
. The gain function then becomes
![ g(\mathbf{q}) = (q_r - \| \mathbf{q}_v \|^2)
tr(\mathbf{B}^T) + 2 tr (\mathbf{q}_v \mathbf{q}_v^T \mathbf{B}^T)
+ 2 q_r tr( [\mathbf{q}_v]_x
\mathbf{B}^T) ](https://latex.codecogs.com/png.image?%5Cdpi%7B110%7D&space;%5Cbg_white&space;%0Ag%28%5Cmathbf%7Bq%7D%29%20%3D%20%28q_r%20-%20%5C%7C%20%5Cmathbf%7Bq%7D_v%20%5C%7C%5E2%29%20tr%28%5Cmathbf%7BB%7D%5ET%29%20%2B%202%20tr%20%28%5Cmathbf%7Bq%7D_v%20%5Cmathbf%7Bq%7D_v%5ET%20%5Cmathbf%7BB%7D%5ET%29%20%2B%202%20q_r%20tr%28%20%5B%5Cmathbf%7Bq%7D_v%5D_x%20%5Cmathbf%7BB%7D%5ET%29%0A)
Putting this expression in terms of its bilinear form, we have
where
![ \mathbf{K}_{4 \times 4} =
\left[ \begin{array}{rr} \sigma & \mathbf{z}^T
\\ \mathbf{z} & \mathbf{S} - \sigma
\mathbf{I}_3 \end{array} \right] ](https://latex.codecogs.com/png.image?%5Cdpi%7B110%7D&space;%5Cbg_white&space;%0A%5Cmathbf%7BK%7D_%7B4%20%5Ctimes%204%7D%20%3D%20%5Cleft%5B%0A%5Cbegin%7Barray%7D%7Brr%7D%0A%5Csigma%20%26%20%5Cmathbf%7Bz%7D%5ET%20%5C%5C%0A%5Cmathbf%7Bz%7D%20%26%20%5Cmathbf%7BS%7D%20-%20%5Csigma%20%5Cmathbf%7BI%7D_3%0A%5Cend%7Barray%7D%0A%5Cright%5D%0A)
where
The optimal quaternion which maximimizes the gain function is the
eigenvector associated with the largest eigenvalue,
, of matrix
# create some vector in the reference frame
n <- 3
sd <- 1e-3
W <- matrix(rnorm(3 * n, sd = ),ncol = 3)
W <- t(apply(W,2,FUN = function(x) {x/norm(x, "2")^2}))
W
#> [,1] [,2] [,3]
#> [1,] -0.3876940 -0.08612243 -0.42998760
#> [2,] -0.2685413 0.47500568 0.03848487
#> [3,] -0.2655570 0.69677187 -0.32195384
# create some rotation matrix and
pitch <- 90
roll <- 0
yaw <- 0
R <- euler_to_rotation(pitch, roll,yaw, units = "degrees")
# rotation matrix
R
#> [,1] [,2] [,3]
#> [1,] 1 0.000000e+00 0.000000e+00
#> [2,] 0 6.123234e-17 -1.000000e+00
#> [3,] 0 1.000000e+00 6.123234e-17
# create vector in body frame and add noise
sd <- 1e-2
V <- t(apply(W,1,function(x) {R %*% x})) + matrix(rnorm(3*n, mean = 0 ,sd = sd),nrow = n)
V
#> [,1] [,2] [,3]
#> [1,] -0.3791908 0.43733015 -0.07604239
#> [2,] -0.2631449 -0.03920862 0.48399961
#> [3,] -0.2604135 0.31035092 0.68793813
The optimal rotation is found by find_rotation
out <- find_rotation(W,V, output = "euler", sd = NA)
out$rotation
#> $pitch
#> [1] 89.26877
#>
#> $roll
#> [1] 179.7568
#>
#> $yaw
#> [1] 179.2509
If standard deviation estimate is given, an estimate of the covariance
matrix for the rotation will be returned.
out <- find_rotation(W,V, output = "euler", sd = sd)
out$rotation
#> $pitch
#> [1] 89.26877
#>
#> $roll
#> [1] 179.7568
#>
#> $yaw
#> [1] 179.2509
out$cov
#> pitch roll yaw
#> pitch 0.01583568 0.01204993 0.02902866
#> roll 0.01204993 0.01242081 0.02620081
#> yaw 0.02902866 0.02620081 0.05957948
adamwbolton/rattitude documentation built on May 6, 2022, 6:33 p.m.
R Package Documentation
Browse R Packages
We want your feedback!
Note that we can't provide technical support on individual packages. You should contact the package authors for that.
rattitude
rattitude has two main functions: (1) inertial-based three-axis accelerometer calibration and (2) attitude determination.
Installation
# install.packages("devtools")
devtools::install_github("adamwbolton/rattitude")
Example
library(rattitude)
Rotations
Rotations can be specified either as rotation matrices, sequences of
Euler angles, or rotation quaternions. One can convert between the three
with the following functions: euler_to_rotation,
euler_to_quaternion, rotation_to_quaternion, rotation_to_euler,
quaternion_to_euler, quaternion_to_rotation. Let’s start with a
rotation of 90 degrees about the x-axis and convert this to a rotation
matrix:
# toy data
pitch <- 90
roll <- 0
yaw <- 0
R <- euler_to_rotation(pitch, roll,yaw, units = "degrees")
# rotation matrix
R
#> [,1] [,2] [,3]
#> [1,] 1 0.000000e+00 0.000000e+00
#> [2,] 0 6.123234e-17 -1.000000e+00
#> [3,] 0 1.000000e+00 6.123234e-17
converting this back to Euler angles
# convert back to euler angles
rotation_to_euler(R)
#> $pitch
#> [1] 90
#>
#> $roll
#> [1] 0
#>
#> $yaw
#> [1] 0
and then to a rotation quaternion
# rotation to quaternion
q <- rotation_to_quaterion(R)
q
#> [1] 0.7071068 0.0000000 0.0000000 0.7071068
and back to Euler angles
quaterion_to_euler(q)
#> $pitch
#> [1] 90
#>
#> $roll
#> [1] 0
#>
#> $yaw
#> [1] 0
Calibration
The calibration for the inertial-based three-axis accelerometers is done through the following first-order model:
where .
For the x-axis accelerometer,
is the bias,
is the sensitivity,
is the coefficient for the cross-axis sensitivity of
,
is the coefficient for the cross-axis sensitivity of
. The sensitivity matrix,
, and the bias vector,
, are given by
Calibration is done through the calibration function which takes
matrices
and
are arguments and returns the estimates of the
sensitivity and bias terms of the model above. Each row of
should have unit norm.
# create sensitivity matrix and bias vector
Beta0 <- c(0,0,0)
Beta <- diag(3) + matrix(rnorm(9,sd = 1e-4),nrow = 3)
# number of observations
n <- 10
# create matrix of gravity vectors
G <- matrix(rnorm(3*n), nrow =n)
G <- t(apply(G,1,FUN = function(x) x/norm(x,"2")))
# simulate responses based on calibration model with some noise
V <- G %*% Beta + Beta0 + matrix(rnorm(3*n, sd = 1e-2), nrow =n)
To fit the calibration model….
cal <- calibration(V,G)
Estimates of the sensitivity and bias terms in the model
cal$coef
#> $BetaHat
#> [,1] [,2] [,3]
#> [1,] 0.999601350 -0.016203819 0.002389500
#> [2,] 0.002422397 0.991612219 0.004893546
#> [3,] 0.005512963 0.007760368 1.002375200
#>
#> $Beta
#> [,1] [,2] [,3]
#> [1,] 1.000076e+00 8.059277e-05 1.135893e-04
#> [2,] 5.456315e-05 9.997552e-01 4.076539e-06
#> [3,] -1.038208e-04 -6.119115e-06 9.999143e-01
Estimates of the gravity vectors given by
cal$Ghat
#> [,1] [,2] [,3]
#> [1,] -0.708042358 0.59581656 0.38242550
#> [2,] -0.115753373 0.96577065 0.18156004
#> [3,] 0.049395167 -1.02113780 -0.01229979
#> [4,] 0.122635690 0.05509749 -0.98369083
#> [5,] -0.003190392 0.70095190 0.71947303
#> [6,] -0.859939419 0.30872718 0.44181834
#> [7,] -0.256087371 -0.94040855 0.18621783
#> [8,] -0.927600534 -0.15038225 -0.28208025
#> [9,] 0.130101505 -0.64665419 0.74144121
#> [10,] 0.971819066 0.27117651 0.07182864
Estimate of
from calibration model
cal$sd
#> [1] 0.01080902
Attitude Estimation
Wahba’s problem seeks to minimize the cost-function
where
is the u-th 3-vector measurement in the reference
frame,
is the corresponding i-th 3-vector measurement in the
body frame
is a
rotation matrix between the reference frame and body
frame. The optimal rotation,
can be found using Davenport’s q-method:
Define the corresponding gain function:
\begin{align}
G(R) & = 1- L(R) \\ & = \sum_{i=1}^n tr(\mathbf{w}_i^T \mathbf{R} \mathbf{v}_i) \\ & =
tr(\mathbf{W}^T \mathbf{R} \mathbf{V}) \\ & =
tr(\mathbf{R} \mathbf{B}^T)
\end{align}
where
Parameterizing the rotation matrix in terms of quaternion, we have
where
is the skew-symmetric matrix of vector
. The gain function then becomes
Putting this expression in terms of its bilinear form, we have
where
where
The optimal quaternion which maximimizes the gain function is the
eigenvector associated with the largest eigenvalue,
, of matrix
# create some vector in the reference frame
n <- 3
sd <- 1e-3
W <- matrix(rnorm(3 * n, sd = ),ncol = 3)
W <- t(apply(W,2,FUN = function(x) {x/norm(x, "2")^2}))
W
#> [,1] [,2] [,3]
#> [1,] -0.3876940 -0.08612243 -0.42998760
#> [2,] -0.2685413 0.47500568 0.03848487
#> [3,] -0.2655570 0.69677187 -0.32195384
# create some rotation matrix and
pitch <- 90
roll <- 0
yaw <- 0
R <- euler_to_rotation(pitch, roll,yaw, units = "degrees")
# rotation matrix
R
#> [,1] [,2] [,3]
#> [1,] 1 0.000000e+00 0.000000e+00
#> [2,] 0 6.123234e-17 -1.000000e+00
#> [3,] 0 1.000000e+00 6.123234e-17
# create vector in body frame and add noise
sd <- 1e-2
V <- t(apply(W,1,function(x) {R %*% x})) + matrix(rnorm(3*n, mean = 0 ,sd = sd),nrow = n)
V
#> [,1] [,2] [,3]
#> [1,] -0.3791908 0.43733015 -0.07604239
#> [2,] -0.2631449 -0.03920862 0.48399961
#> [3,] -0.2604135 0.31035092 0.68793813
The optimal rotation is found by find_rotation
out <- find_rotation(W,V, output = "euler", sd = NA)
out$rotation
#> $pitch
#> [1] 89.26877
#>
#> $roll
#> [1] 179.7568
#>
#> $yaw
#> [1] 179.2509
If standard deviation estimate is given, an estimate of the covariance matrix for the rotation will be returned.
out <- find_rotation(W,V, output = "euler", sd = sd)
out$rotation
#> $pitch
#> [1] 89.26877
#>
#> $roll
#> [1] 179.7568
#>
#> $yaw
#> [1] 179.2509
out$cov
#> pitch roll yaw
#> pitch 0.01583568 0.01204993 0.02902866
#> roll 0.01204993 0.01242081 0.02620081
#> yaw 0.02902866 0.02620081 0.05957948
R Package Documentation
Browse R Packages
We want your feedback!
Note that we can't provide technical support on individual packages. You should contact the package authors for that.
Embedding an R snippet on your website
Add the following code to your website.
For more information on customizing the embed code, read Embedding Snippets.