In timjmiller/wham: Woods Hole Assessment Model (WHAM)

knitr::opts_chunk$set(
  collapse = TRUE,
  comment = "#>"
)
#wham.dir <- find.package("wham")
#knitr::opts_knit$set(root.dir = file.path(wham.dir,"extdata"))

In this vignette we walk through an example using the wham (WHAM = Woods Hole Assessment Model) package to run a state-space age-structured stock assessment model. WHAM is a generalization of code written for Miller et al. (2016) and Xu et al. (2018), and in this example we apply WHAM to the same stock, Southern New England / Mid-Atlantic Yellowtail Flounder.

This is the 2nd wham example, which builds off model m4 from example 1 (full state-space model, numbers at all ages are random effects, logistic normal age-compositions). We assume you already have wham installed. If not, see the Introduction. The simpler 1st example, without environmental effects, is available as a R script and vignette.

In example 2, we demonstrate how to specify and run WHAM with varying

• recruitment models (random, Bev-Holt, Ricker)

• environmental covariate (Cold Pool Index, CPI) process models (random walk, AR1), and

• how the CPI affects recruitment (controlling or limiting)

As in example 1, we check that each model converges (check_convergence()), plot diagnostics, results, and reference points (plot_wham_output()), and compare models using AIC and Mohn's rho (compare_wham_models()).

1. Prepare wham

Open R and load the wham package:

library(wham)

is.repo <- try(pkgload::load_all(compile=FALSE)) #this is needed to build the vignettes without the new version of wham installed.
if(is.character(is.repo)) library(wham) #not building webpage
#note that if plots are not yet pushed to the repo, they will not show up in the html.
wham.dir <- find.package("wham")

For a clean, runnable .R script, look at ex2_CPI_recruitment.R in the example_scripts folder of the wham package. You can run this entire example script with:

wham.dir <- find.package("wham")
source(file.path(wham.dir, "example_scripts", "ex2_CPI_recruitment.R"))

Let's create a directory for this analysis:

# choose a location to save output, otherwise will be saved in working directory
write.dir <- "choose/where/to/save/output" #e.g., tempdir(check=TRUE)
dir.create(write.dir)
setwd(write.dir)

write.dir <- tempdir(check=TRUE)
setwd(write.dir)

WHAM was originally built by modifying the ADMB-based ASAP model code (Legault and Restrepo 1999), and is designed to take an ASAP3 .dat file as input. We generally assume in wham that you have an existing ASAP3 .dat file. If you are not familiar with ASAP3 input files, see the ASAP documentation and code. For this vignette, an example ASAP3 input file is provided, ex2_SNEMAYT.dat. We will also need a data file with an environmental covariate, the Cold Pool Index, CPI.csv.

Read in ex2_SNEMAYT.dat and CPI.csv to R:

wham.dir <- find.package("wham")
asap3 <- read_asap3_dat(file.path(wham.dir,"extdata","ex2_SNEMAYT.dat"))
env.dat <- read.csv(file.path(wham.dir,"extdata","CPI.csv"), header=T)

path_to_examples <- system.file("extdata", package="wham")
env.dat <- read.csv(file.path(path_to_examples,"CPI.csv"), header=T)

We generally abbreviate 'environmental covariate' as ecov in the code. In this example, the ecov data file has columns for observations (CPI), standard error (CPI_sigma), and year (Year). Observations and year are always required. Standard error can be treated as fixed/data with yearly values (as here) or one overall value shared among years. It can also be estimated as a parameter(s), likewise either as yearly values or one overall value.

head(env.dat)

2. Specify models

Now we specify how the 7 models treat recruitment, the CPI process, and how the CPI affects recruitment:

Ecov_how <- paste0(
  c("none", "controlling-", "none", "limiting-", "limiting-", "controlling-", "controlling-"), 
  c("", "lag-1-", "", rep("lag-1-",4)),
  c("", "linear", "", rep("linear", 4)))

df.mods <- data.frame(Recruitment = c(2,2,3,3,3,3,4),
                      Ecov_process = c(rep("rw",4),rep("ar1",3)),
                      Ecov_how = Ecov_how, stringsAsFactors=FALSE)
n.mods <- dim(df.mods)[1]
df.mods$Model <- paste0("m",1:n.mods)
df.mods <- dplyr::select(df.mods, Model, tidyselect::everything()) # moves Model to first col

Look at the model table. The Ecov_how is a a more recent character string approach to defining environmental effects on recruitment.

df.mods

We specify the options for modeling recruitment and any environmental covariate(s) using the prepare_wham_input() function. WHAM provides 4 options for recruitment (recruit_model):

1. random walk,
2. random about mean,
3. Beverton-Holt, and
4. Ricker.

The environmental covariate options are fed to prepare_wham_input() as a list, ecov:

  m=1 # example for first model
  ecov <- list(
    label = "CPI",
    mean = as.matrix(env.dat$CPI),
    logsigma = as.matrix(log(env.dat$CPI_sigma)),
    year = env.dat$Year,
    use_obs = matrix(1, ncol=1, nrow=dim(env.dat)[1]), # use all obs (=1)
    process_model = df.mods$Ecov_process[m], # "rw" or "ar1"
    recruitment_how = matrix(df.mods$Ecov_how[m],1,1)) #matrix for number of stocks (1) and number of Ecovs (1)

There are currently 2 options for the ecov process model (ecov$process_model): 1) random walk ('rw'), and 2) autoregressive ('ar1'). Recent versions of WHAM now specify effects of covariates on recruitment, natural mortality, catchability, and movement using character strings. For recruitment we specify recruitment_how for the mechanistic affect on recruitment, the time lag between the covariate and recruitment, and the order of the orthogonal polynomial effect. The options for the mechanistic effect follow Iles and Beverton (1998) and Xu et al. (2018):

1. "controlling" (density-independent mortality),
2. "limiting" (carrying capacity, e.g. ecov determines amount of suitable habitat),
3. "lethal" (threshold, i.e. R --> 0 at some ecov value),
4. "masking" (metabolic/growth, ecov decreases dR/dS), and
5. "directive" (e.g., behavioral).

In Ecov_how we specify the lag of 1 for the CPI so that CPI in year t affects recruitment in year t + 1. We also specify a first order polynomial ("linear" or "poly-1"). For no effect of the covariate, but still keeping the state-space model estimation for the covariate, Ecov_how= "none".

You can set ecov = NULL or process_model= NA to fit the model without environmental covariate data, but note that here we fit the ecov data even for models without an ecov effect on recruitment (m1 and m3) so that we can compare them via AIC (need to have the same data in the likelihood).

Options are described in the set_ecov help page. Not all mechanistic effects options are implemented for every recruitment model.

?set_ecov

3. Run the models

for(m in 1:n.mods){
  # set up environmental covariate data and model options
  ecov <- list(
    label = "CPI",
    mean = as.matrix(env.dat$CPI),
    logsigma = as.matrix(log(env.dat$CPI_sigma)),
    year = env.dat$Year,
    use_obs = matrix(1, ncol=1, nrow=dim(env.dat)[1]), # use all obs (=1)
    process_model = df.mods$Ecov_process[m], # "rw" or "ar1"
    recruitment_how = matrix(df.mods$Ecov_how[m],1,1)) #matrix for number of stocks (1) and number of Ecovs (1)

  # (not used in this vignette) can set ecov = NULL to fit model without ecov data
  if(is.na(df.mods$ecov_process[m])) ecov = NULL 

  # generate wham input from ASAP3 and ecov data
  input <- prepare_wham_input(asap3, recruit_model = df.mods$Recruitment[m],
                              model_name = "Ex 2: SNEMA Yellowtail Flounder with CPI effects on R",
                              ecov = ecov,
                              NAA_re = list(sigma="rec+1", cor="iid"),
                              age_comp = "logistic-normal-pool0") # logistic normal pool 0 obs

  # Selectivity = logistic, not age-specific as in ex1
  #   2 pars per block instead of n.ages
  #   sel pars of indices 4/5 fixed at 1.5, 0.1 (specified via neg phase in ex2_SNEMAYT.dat)
  input$par$logit_selpars[1:4,7:8] <- 0 # last 2 rows will not be estimated (mapped to NA)

  # Fit model
  mod <- fit_wham(input, do.retro=TRUE, do.osa=TRUE)

  # Save model
  saveRDS(mod, file=paste0(df.mods$Model[m],".rds"))

  # Plot output in new subfolder
  plot_wham_output(mod=mod, dir.main=file.path(getwd(),df.mods$Model[m]), out.type='html')
}

4. Check for convergence

data(vign2_conv)
data(vign2_res)

Collect all models into a list.

mod.list <- paste0(df.mods$Model,".rds")
mods <- lapply(mod.list, readRDS)

We need to check that the models converged. The maximum absolute gradient should be very close to 0 and SE estimates should be calculable (invertible Hessian, TMB::sdreport() succeeds). All models seem to have converged and have a positive definite Hessian.

vign2_conv <- lapply(mods, function(x) capture.output(check_convergence(x)))
for(m in 1:n.mods) cat(paste0("Model ",m,":"), vign2_conv[[m]], "", sep='\n')

for(m in 1:7) cat(paste0("Model ",m,":"), vign2_conv[[m]], "", sep='\n')

5. Compare models

Let's first make the results table prettier.

df.mods$Recruitment <- dplyr::recode(df.mods$Recruitment, `2`='Random', `3`='Bev-Holt', `4`='Ricker')
df.mods$Ecov_how <- c("---", "Controlling", "---", "Limiting", "Limiting", "Controlling", "Controlling")

Now get the convergence information.

opt_conv = 1-sapply(mods, function(x) x$opt$convergence)
ok_sdrep = sapply(mods, function(x) if(x$na_sdrep==FALSE & !is.na(x$na_sdrep)) 1 else 0)
df.mods$conv <- as.logical(opt_conv)
df.mods$pdHess <- as.logical(ok_sdrep)
df.mods$NLL <- sapply(mods, function(x) round(x$opt$objective,3))

Only calculate AIC and Mohn's rho for converged models.

not_conv <- !df.mods$conv | !df.mods$pdHess
mods2 <- mods
mods2[not_conv] <- NULL
df.aic.tmp <- as.data.frame(compare_wham_models(mods2, table.opts=list(sort=FALSE, calc.rho=T))$tab)
df.aic <- df.aic.tmp[FALSE,]
ct = 1
for(i in 1:n.mods){
  if(not_conv[i]){
    df.aic[i,] <- rep(NA,5)
  } else {
    df.aic[i,] <- df.aic.tmp[ct,]
    ct <- ct + 1
  }
}
df.mods <- cbind(df.mods, df.aic)
df.mods <- df.mods[order(df.mods$dAIC, na.last=TRUE),]
df.mods[is.na(df.mods$AIC), c('dAIC','AIC','rho_R','rho_SSB','rho_Fbar')] <- "---"
rownames(df.mods) <- NULL

Print and save the results table. m6 has the lowest AIC (Bev-Holt recruitment, CPI modeled as AR1, controlling effect of CPI on recruitment), but m5 and m7 have similar AIC values.

save("df.mods", file="vign2_res.RData")
df.mods

vign2_res

6. Results

There are various options for creating WHAM output. The default is to create a self-contained html file using Rmarkdown and individual plot files (.png) that are organised within subdirectories of plots_png. The html file also includes tables of estimates for fundamental parameters and abundance and fishing mortality at age. On Windows you may need to use Chrome or Internet Explorer to view the .html (there have been issues using Firefox on Windows but not Linux).

# save output plots in subfolder for each model
for(m in 1:n.mods) plot_wham_output(mod=mods[[m]], dir.main=file.path(getwd(), df.mods$Model[m]), out.type='html')

Cold Pool Index (CPI)

Models that included an effect of the Cold Pool Index on recruitment were strongly supported by AIC over models without CPI effects (m2 and m4-7 lower AIC than m1 and m3). Note that we can compare models with and without a CPI effect on recruitment using AIC because we also fit the CPI data in the models without the effect (m1 and m3).

Comparing m4 and m5 demonstrates that the CPI was best modeled as an AR1 process (m5) instead of a random walk (m4), since this was the only difference between the two models and m5 had lower AIC. The one-step-ahead residuals for the CPI from m5 (right) are similar in distribution. The linear trend in the OSA residuals with observed value for m5 is due to the best prediction of the next observation being near the mean of the process in this case because the estimated autocorrelation parameter is near 0:

{ width=45% }{ width=45% }

As we saw from the table of results, all the models produced similar Mohn's $\rho$ values for SSB, F, and recruitment. Below are the relative retrospective peels for the model without any SSB or CPI effects on recruitment (m1, left) and the best model that included CPI and SSB effects on recruitment, (m6, right).

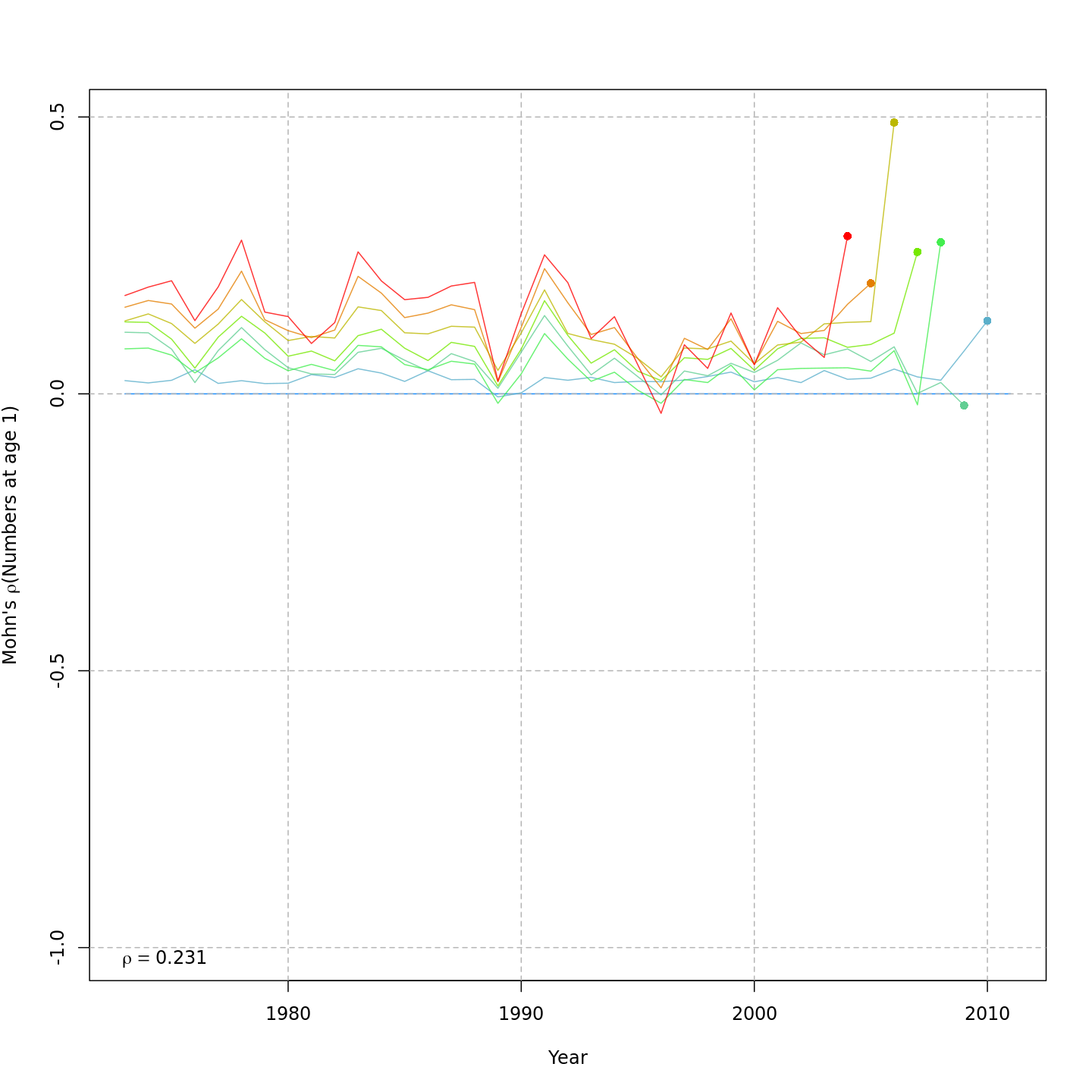{ width=45% }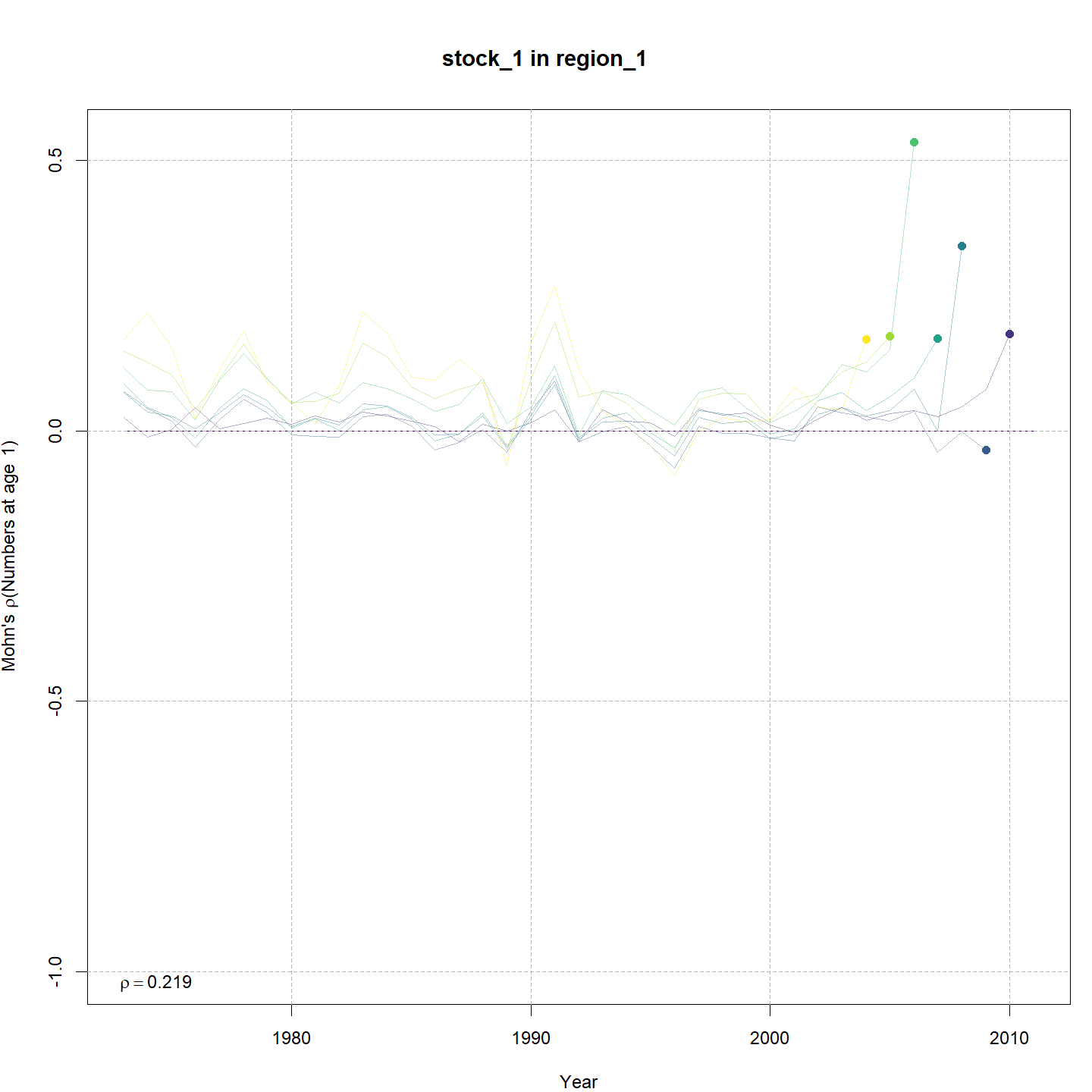{ width=45% }

Recruitment

A Beverton-Holt stock-recruitment assumption was preferred over random recruitment (m3 lower AIC than m1). Models that included both Bev-Holt and CPI effects on recruitment had lower AIC than the model with Bev-Holt but without the CPI (m4 vs. m3). Adding the CPI effect to the Bev-Holt explains some of the variability around the stock-recruit curve, which resulted in m4 (right) estimating lower $\sigma_R$ than m3 (left).

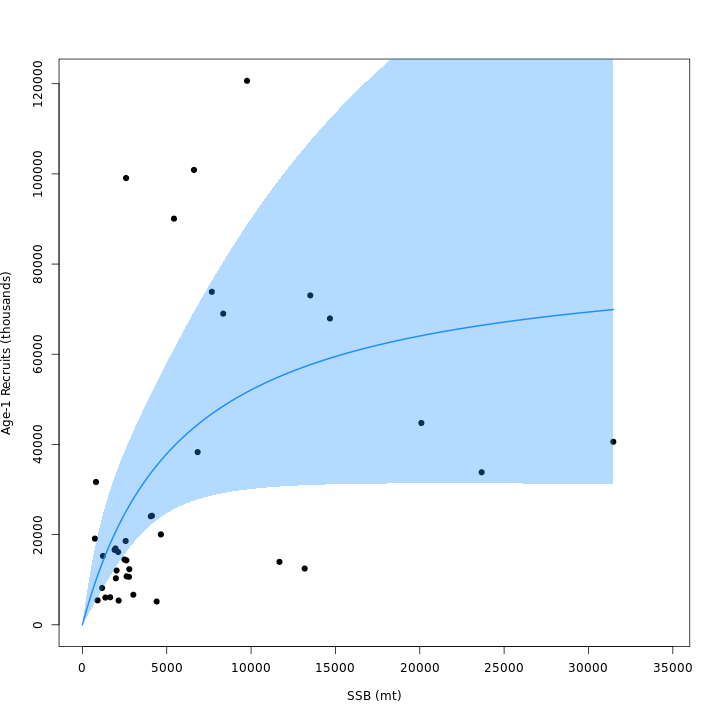{ width=45% }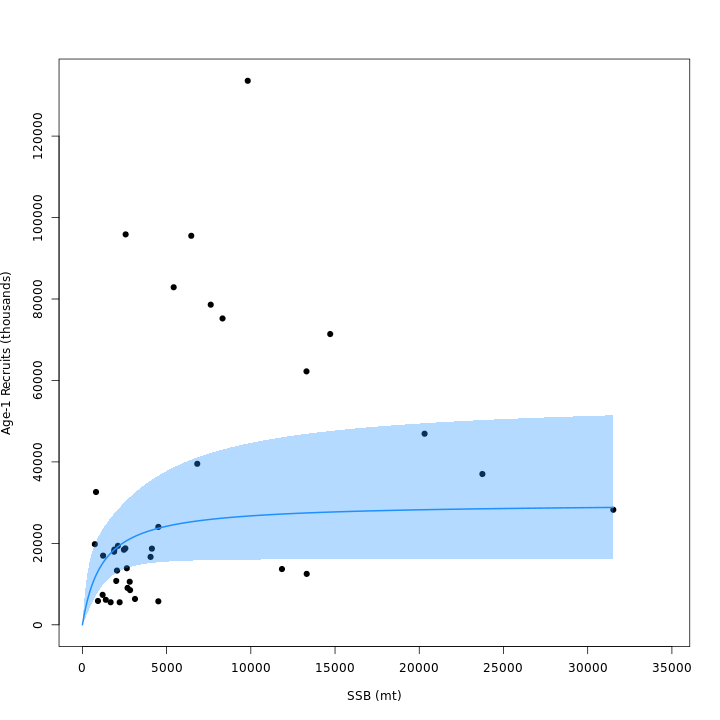{ width=45% }

Stock status

Whether or not to include a stock-recruit function and/or the CPI did not have a great influence on estimated stock status using SPR-based reference points. Specifically, the models hardly differed in their estimation of the probability that the stock was overfished, $Pr[SSB < 0.5 \: SSB_{40\%}]$. All models estimated with 100% probability that the stock was not experiencing overfishing in 2011, $F < F_{40\%}$.

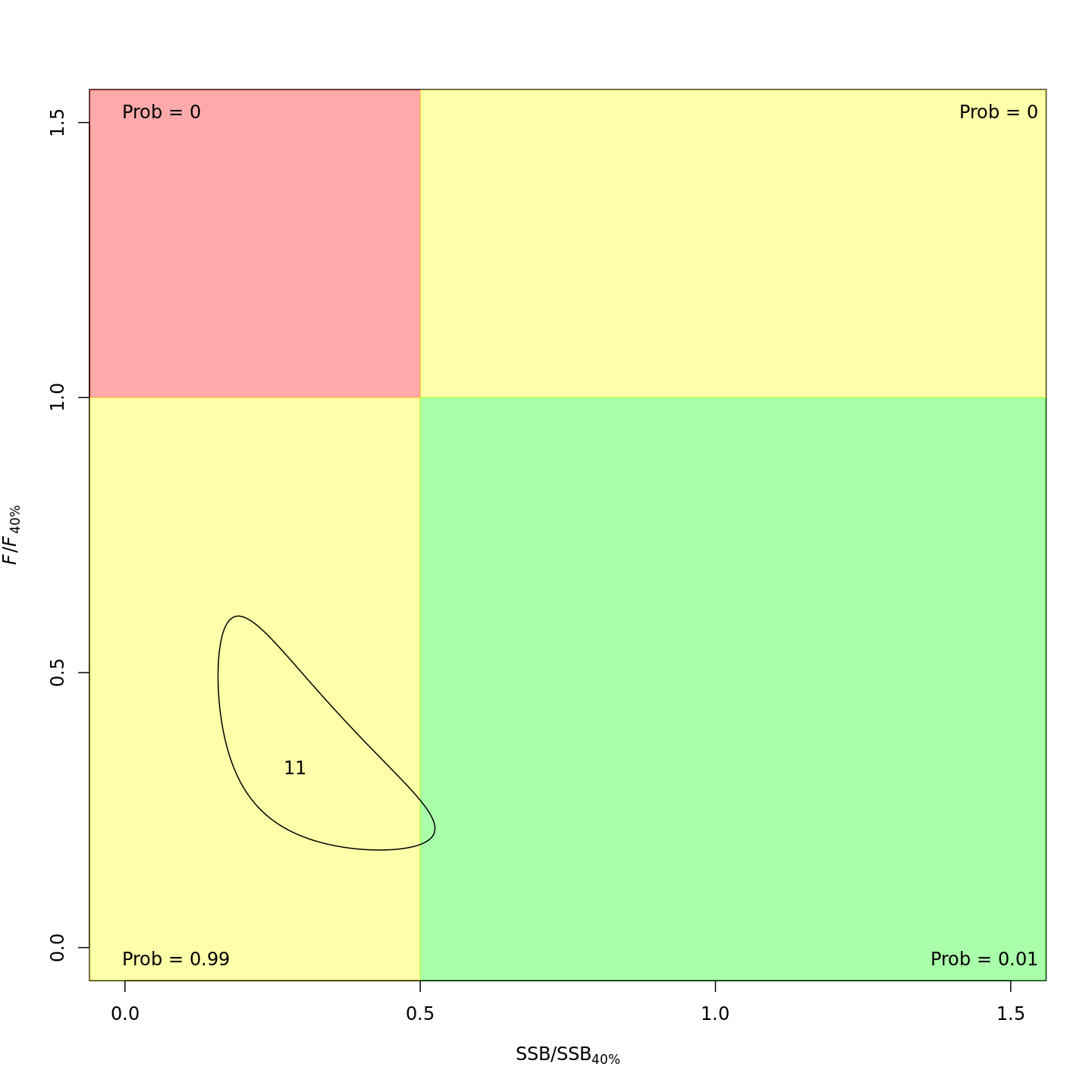{ width=45% }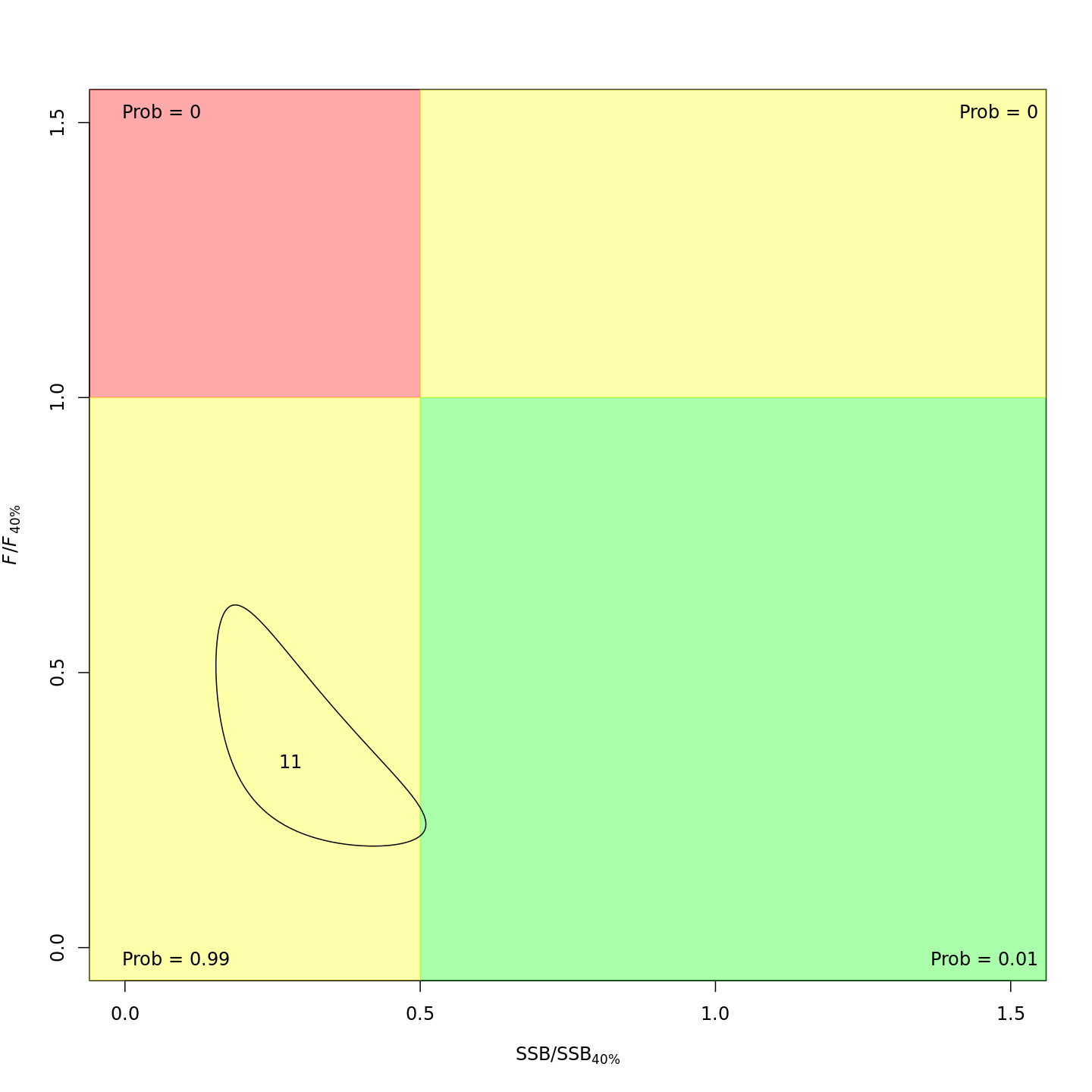{ width=45% }

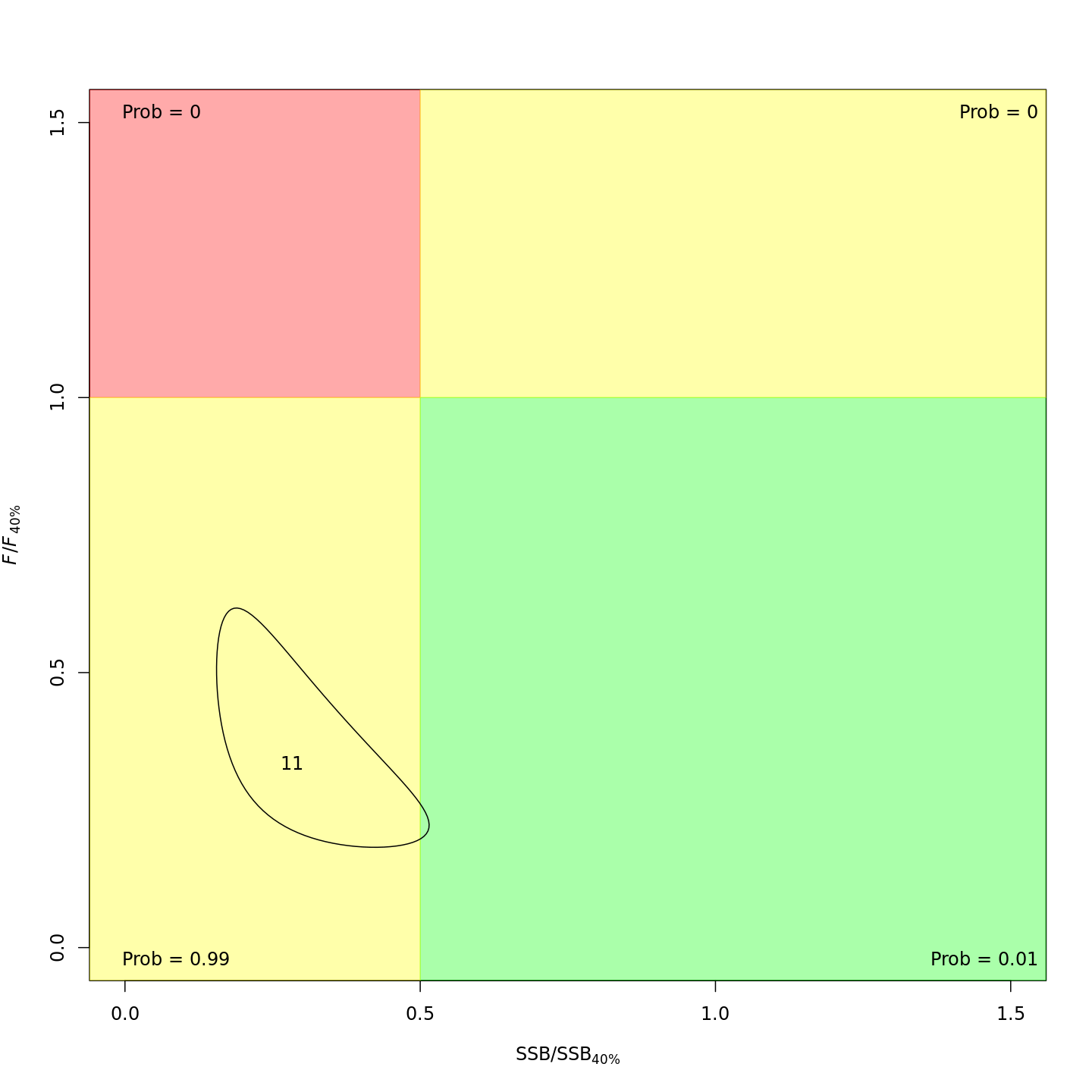{ width=30% }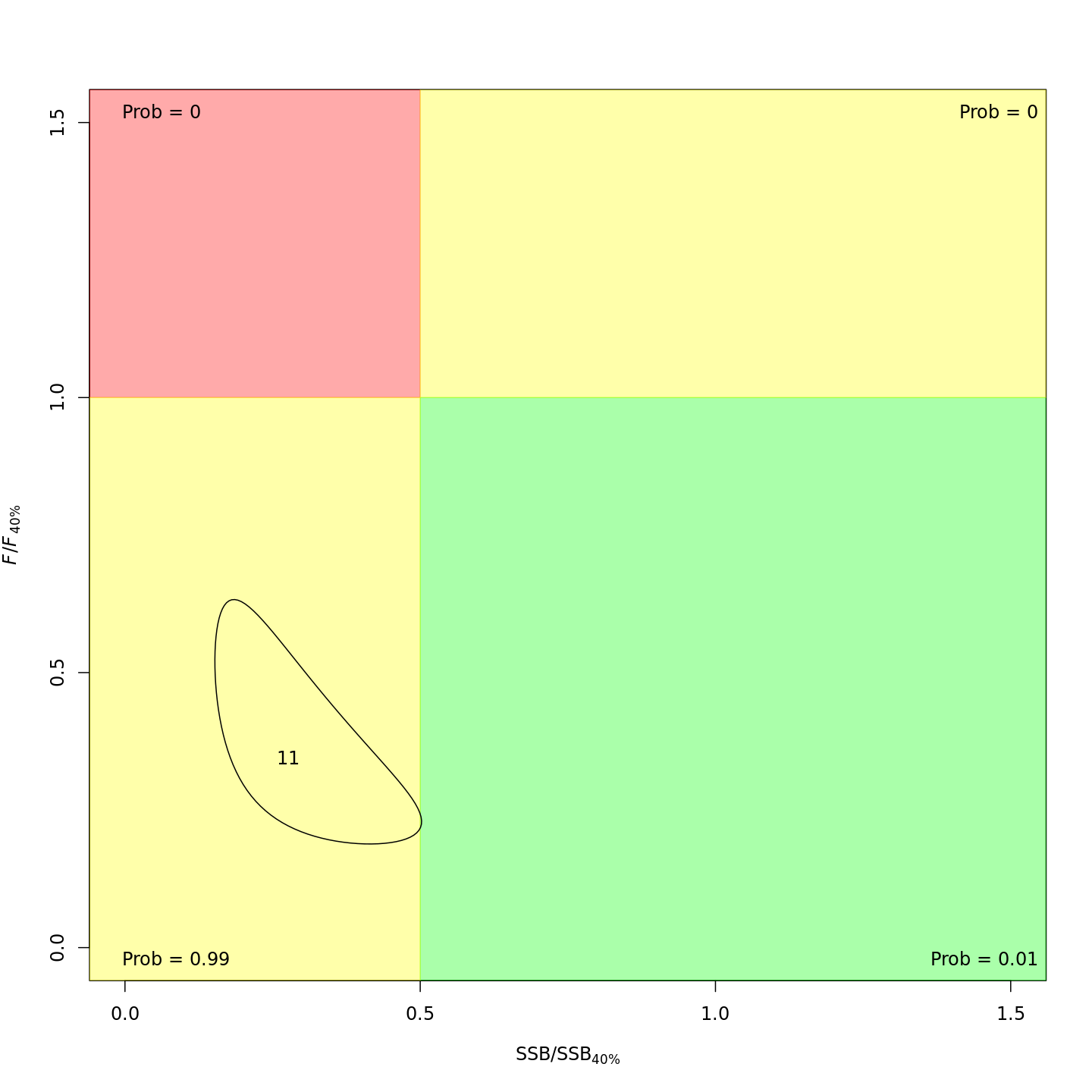{ width=30% }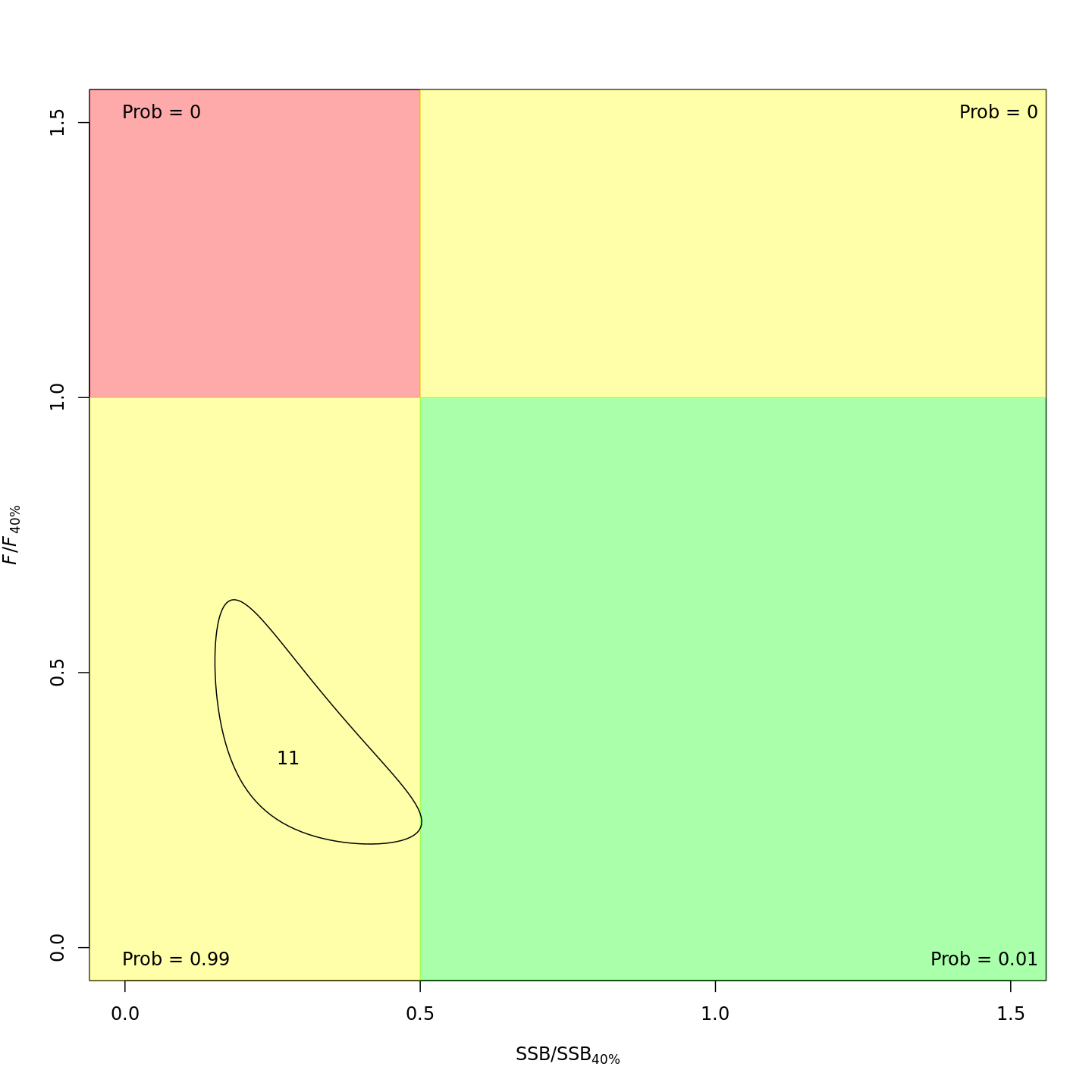{ width=30% }

When determined relative MSY-based reference points, status is more optimistic: { width=30% }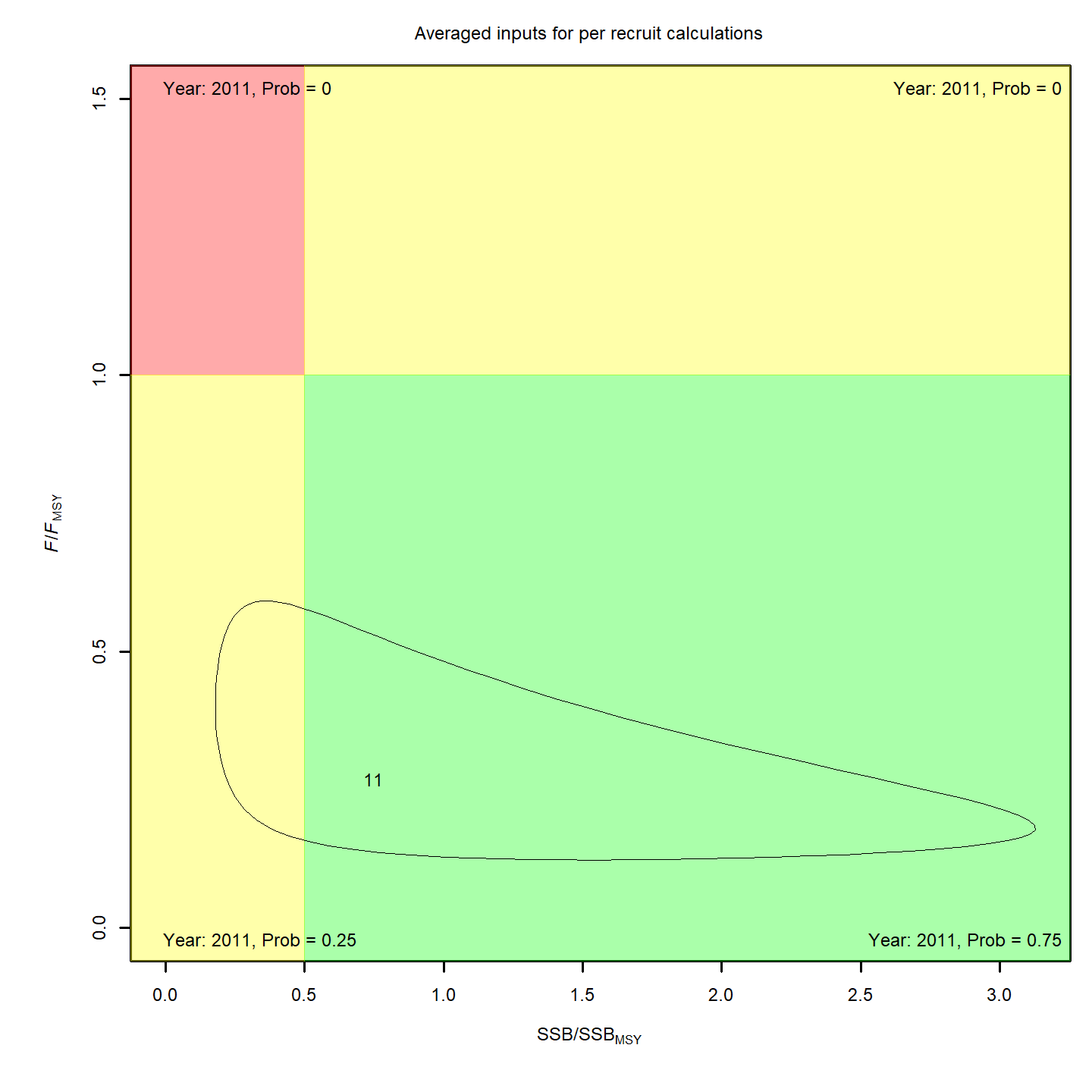{ width=30% }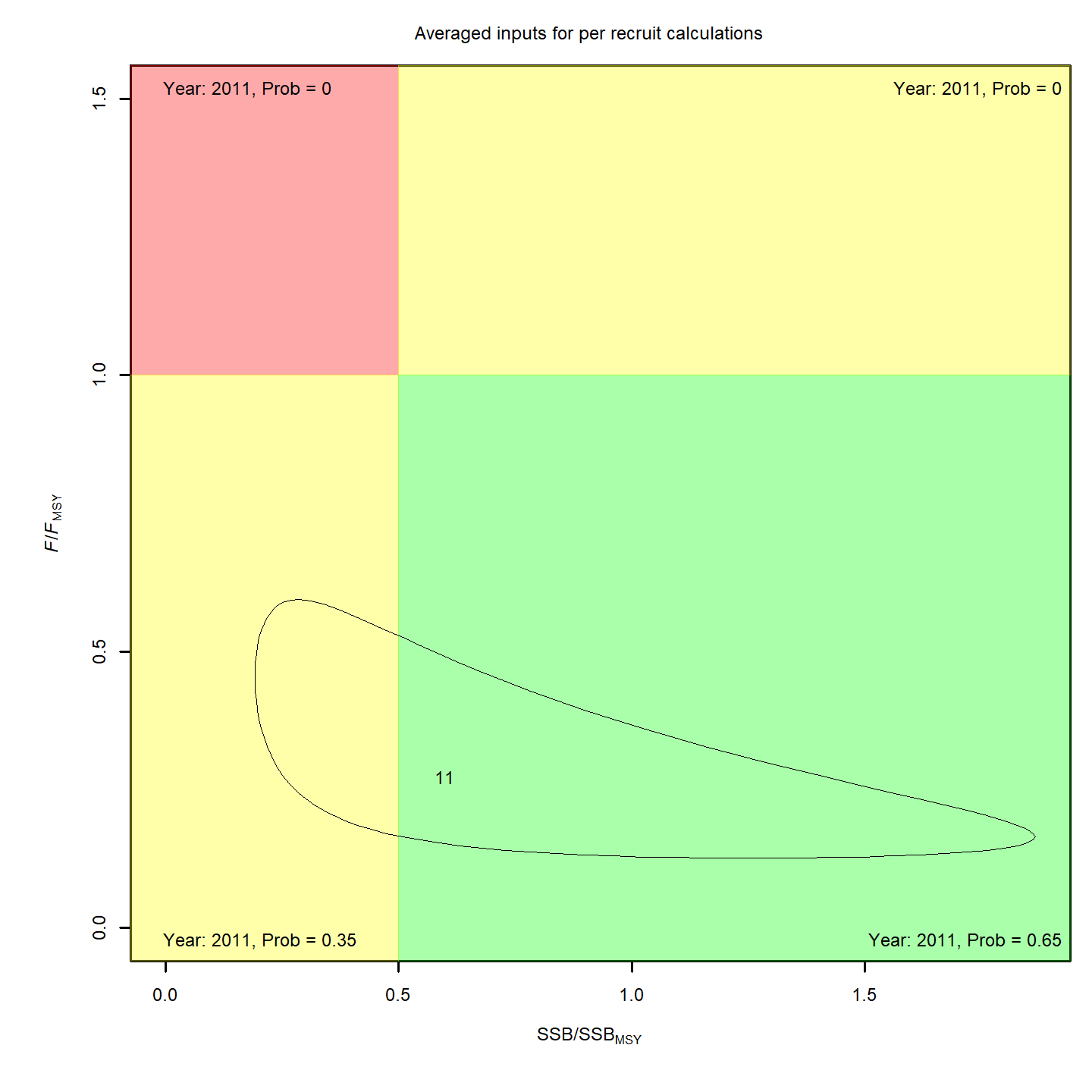{ width=30% }

timjmiller/wham documentation built on Feb. 4, 2025, 10:31 p.m.