In timjmiller/wham: Woods Hole Assessment Model (WHAM)
knitr::opts_chunk$set(
collapse = TRUE,
comment = "#>"
)
# wham.dir <- find.package("wham")
# knitr::opts_knit$set(root.dir = file.path(wham.dir,"extdata"))
is.repo <- try(pkgload::load_all(compile=FALSE)) #this is needed to build the vignettes without the new version of wham installed.
if(is.character(is.repo)) library(wham) #not building webpage
#note that if plots are not yet pushed to the repo, they will not show up in the html.
wham.dir <- find.package("wham")
library(knitr)
library(kableExtra)
In this vignette we walk through an example using the wham (WHAM = Woods Hole Assessment Model) package to run a state-space age-structured stock assessment model. WHAM is a generalization of code written for Miller et al. (2016) and Xu et al. (2018), and in this example we apply WHAM to the same stock, Southern New England / Mid-Atlantic Yellowtail Flounder.
This is the 6th WHAM example, which blends aspects from Ex 1, Ex 2, and Ex 5. We assume you already have wham installed. If not, see the Introduction. The simpler 1st example is available as a R script and vignette.
As in example 1:
- Stock: Southern New England-Mid Atlantic (SNEMA) yellowtail flounder
- Data: 1973-2011, 1 fishery and 2 indices
- Age compositions: logistic normal, treating observations of zero as missing (
age_comp = "logistic-normal-miss0")
- Selectivity: age-specific
As in example 2:
- Beverton-Holt recruitment (
recruit_model = 3)
- Environmental covariate (ecov) modeled as an AR1 process (
ecov$process_model = 'ar1')
- Compare with and w/o ecov having a "limiting" (carrying capacity) effect on recruitment (
ecov$how = 2)
As in example 4:
- Age-specific selectivity with some ages fixed at 1 (fishery: 4-5, index1: 4, index2: 2-4)
As in example 5:
- Environmental covariate: Gulf Stream Index (GSI)
- 2D AR1 deviations by age and year (random effects)
Example 6 highlights WHAM's options for treating the yearly transitions in numbers-at-age (i.e. survival):
- Deterministic (as in statistical catch-at-age models, recruitment in each year estimated as independent fixed effect parameters)
- Recruitment deviations (from Bev-Holt expectation) are random effects
- independent
- AR1 deviations by year (autocorrelated)
- "Full state-space model" (survival of all ages are random effects)
- independent
- AR1 deviations by age
- AR1 deviations by year
- 2D AR1 deviations by age and year
1. Load data
Open R and load wham and other useful packages:
library(wham)
library(tidyr)
library(dplyr)
For a clean, runnable .R script, look at ex6_NAA.R in the example_scripts folder of the wham package.
You can run this entire example script with:
wham.dir <- find.package("wham")
source(file.path(wham.dir, "example_scripts", "ex6_NAA.R"))
Let's create a directory for this analysis:
# choose a location to save output, otherwise will be saved in working directory
write.dir <- "choose/where/to/save/output" # need to change e.g., tempdir(check=TRUE)
dir.create(write.dir)
setwd(write.dir)
We need the same ASAP data file as in example 1, and the environmental covariate (Gulf Stream Index, GSI).
Read in ex1_SNEMAYT.dat and GSI.csv:
asap3 <- read_asap3_dat(file.path(wham.dir,"extdata","ex2_SNEMAYT.dat"))
env.dat <- read.csv(file.path(wham.dir,"extdata","GSI.csv"), header=T)
head(env.dat)
As in example 5, the GSI data file does not have a standard error estimate, either for each yearly observation or one overall value. In such a case, WHAM can estimate the observation error for the environmental covariate, either as one overall value, $\sigma_{GSI}$, or yearly values as random effects, $\mathrm{log}\sigma_{{GSI}y} \sim \mathcal{N}(\mathrm{log}\sigma{GSI}, \sigma^2_{\sigma_{GSI}})$. In this example we choose the simpler option and estimate one observation error parameter, shared across years.
2. Specify models
Now we specify several models with different options for the numbers-at-age (NAA) transitions, i.e. survival:
df.mods <- data.frame(NAA_cor = c('---','iid','ar1_y','iid','ar1_a','ar1_y','2dar1','iid','ar1_y','iid','ar1_a','ar1_y','2dar1'),
NAA_sigma = c('---',rep("rec",2),rep("rec+1",4),rep("rec",2),rep("rec+1",4)),
R_how = paste0(c(rep("none",7),rep("limiting-lag-1-linear",6))), stringsAsFactors=FALSE)
n.mods <- dim(df.mods)[1]
df.mods$Model <- paste0("m",1:n.mods)
df.mods <- df.mods %>% select(Model, everything()) # moves Model to first col
Look at the model table:
df.mods
3. Numbers-at-age options
To specify the options for modeling NAA transitions, include an optional list argument, NAA_re, to the prepare_wham_input function (see the prepare_wham_input help page). ASAP3 does not estimate random effects, and therefore these options are not specified in the ASAP data file. By default (NAA_re is NULL or not included), WHAM fits a traditional statistical catch-at-age model (NAA = predicted NAA for all ages, i.e. survival is deterministic). To fit a state-space model, we must specify NAA_re.
NAA_re is a list with the following entries:
$sigma: Which ages allow deviations from pred_NAA? Common options are specified with strings."rec": Recruitment deviations are random effects, survival of all other ages is deterministic"rec+1": Survival of all ages is stochastic ("full state space model"), with 2 estimated $\sigma_a$, one for recruitment and one shared among other ages$cor: Correlation structure for the NAA deviations. Options are:"iid": NAA deviations vary by year and age, but uncorrelated."ar1_a": NAA deviations correlated by age (AR1)."ar1_y": NAA deviations correlated by year (AR1)."2dar1": NAA deviations correlated by year and age (2D AR1, as for $M$ in example 5).
Alternatively, you can specify a more complex configuration of sigma parameter estimation via NAA_re$sigma_map as an array (n_stocks x n_regions x n_ages) of integers (and NAs to fix parameters). For example (with 1 stock and 1 region here), NAA_re$sigma = array(c(1,2,2,3,3,3), dim = c(1,1,6)) will estimate three $\sigma$ parameters, with recruitment (age-1) deviations having their own $\sigma_R$, ages 2-3 sharing $\sigma_2$, and ages 4-6 sharing $\sigma_3$.
To fit model m1 (SCAA) we do not have to supply anything:
NAA_re <- NULL # or simply leave out of call to prepare_wham_input
To fit model m3, recruitment deviations are correlated random effects:
NAA_re <- list(sigma="rec", cor="ar1_y")
And to fit model m7, numbers at all ages are random effects correlated by year AND age:
NAA_re <- list(sigma="rec+1", cor="2dar1")
4. Linking recruitment to an environmental covariate (GSI)
As described in example 2, the environmental covariate options are fed to prepare_wham_input as a list, ecov. This example differs from example 2 in that:
ecov$logsigma = "est_1" estimates the GSI observation error ($\sigma_{GSI}$, one overall value for all years like in example 5). The other option is "est_re" to allow the GSI observation error to have yearly fluctuations (random effects). The Cold Pool Index in example 2 had yearly observation errors given, so this was not necessary.ecov$R_how = matrix("none",1,1) or ecov$R_how = NULL estimates the GSI time-series model (AR1) for models without a GSI-Recruitment effect, in order to compare AIC with models that do include the effect. Setting ecov$R_how = matrix("limiting-lag-1-linear,1,1) specifies that the GSI iyear $t$ affects the Beverton-Holt $\beta$ parameter ("limiting" / carrying capacity effect) in year $t+1$ linearly (on log scale).
For example, the ecov list for models m8-m13 with the linear GSI-$\beta$ effect:
ecov <- list(
label = "GSI",
mean = as.matrix(env.dat$GSI),
logsigma = 'est_1', # estimate obs sigma, 1 value shared across years
year = env.dat$year,
use_obs = matrix(1, ncol=1, nrow=dim(env.dat)[1]), # use all obs (=1)
process_model = 'ar1', # "rw" or "ar1"
R_how = matrix("limiting-lag-1-linear",1,1)) # n_Ecov x n_stocks x n_ages x n_regions
Note that you can set ecov = NULL to fit the model without environmental covariate data, but here we fit the ecov data even for models without the GSI effect on recruitment (m1-m7) so that we can compare them via AIC (need to have the same data in the likelihood). We accomplish this by setting ecov$R_how = matrix("none",1,1) and ecov$process_model = "ar1".
5. Run all models
All models use the same options for expected recruitment (Beverton-Holt stock-recruit function) and selectivity (age-specific, with one or two ages fixed at 1). We specify recruitment decoupling only for consistency with the original implicit assumption in WHAM.
mods <- vector("list",n.mods)
for(m in 1:n.mods){
NAA_list <- list(cor=df.mods[m,"NAA_cor"], sigma=df.mods[m,"NAA_sigma"], decouple_recruitment = FALSE)
if(NAA_list$sigma == '---') NAA_list = NULL
ecov <- list(
label = "GSI",
mean = as.matrix(env.dat$GSI),
logsigma = 'est_1', # estimate obs sigma, 1 value shared across years
year = env.dat$year,
use_obs = matrix(1, ncol=1, nrow=dim(env.dat)[1]), # use all obs (=1)
process_model = 'ar1', # "rw" or "ar1"
recruitment_how = matrix(df.mods$R_how[m])) # n_Ecov x n_stocks
input <- suppressWarnings(prepare_wham_input(asap3, recruit_model = 3, # Bev Holt recruitment
model_name = "Ex 6: Numbers-at-age",
selectivity=list(model=rep("age-specific",3), re=c("none","none","none"),
initial_pars=list(c(0.1,0.5,0.5,1,1,1),c(0.5,0.5,0.5,1,0.5,0.5),c(0.5,0.5,1,1,1,1)),
fix_pars=list(4:6,4,3:6)),
NAA_re = NAA_list,
ecov=ecov,
age_comp = "logistic-normal-miss0")) # logistic normal, treat 0 obs as missing
# Fit model
mods[[m]] <- fit_wham(input, do.retro=T, do.osa=F)
# Save model
saveRDS(mods[[m]], file=paste0(df.mods$Model[m],".rds"))
# If desired, do projections
# mod_proj <- project_wham(mod)
# saveRDS(mod_proj, file=paste0(df.mods$Model[m],"_proj.rds"))
}
6. Compare models
#data(vign6_res) #not needed
Get model convergence and stats.
opt_conv = 1-sapply(mods, function(x) x$opt$convergence)
ok_sdrep = sapply(mods, function(x) if(x$na_sdrep==FALSE & !is.na(x$na_sdrep)) 1 else 0)
df.mods$conv <- as.logical(opt_conv)
df.mods$pdHess <- as.logical(ok_sdrep)
Only calculate AIC and Mohn's rho for converged models.
df.mods$runtime <- sapply(mods, function(x) x$runtime)
df.mods$NLL <- sapply(mods, function(x) round(x$opt$objective,3))
not_conv <- !df.mods$conv | !df.mods$pdHess
mods2 <- mods
mods2[not_conv] <- NULL
df.aic.tmp <- as.data.frame(compare_wham_models(mods2, table.opts=list(sort=FALSE, calc.rho=TRUE))$tab)
df.aic <- df.aic.tmp[FALSE,]
ct = 1
for(i in 1:n.mods){
if(not_conv[i]){
df.aic[i,] <- rep(NA,5)
} else {
df.aic[i,] <- df.aic.tmp[ct,]
ct <- ct + 1
}
}
df.aic[,1:2] <- format(round(df.aic[,1:2], 1), nsmall=1)
df.aic[,3:5] <- format(round(df.aic[,3:5], 3), nsmall=3)
df.aic[grep("NA",df.aic$dAIC),] <- "---"
df.mods <- cbind(df.mods, df.aic)
rownames(df.mods) <- NULL
Look at results table.
df.mods
vign6_res
Save results table.
write.csv(df.mods, file="ex6_table.csv",quote=F, row.names=F)
Plot output for models that converged.
mods[[1]]$env$data$recruit_model = 2 # m1 (SCAA) didn't actually fit a Bev-Holt
for(m in which(!not_conv)){
plot_wham_output(mod=mods[[m]], dir.main=file.path(getwd(),paste0("m",m))) #html by default
}
7. Results
Two models had very similar AIC and were overwhelmingly supported relative to the other models (bold in table below): m11 (all NAA are random effects with correlation by age, GSI-Recruitment effect) and m13 (all NAA are random effects with correlation by age and year, GSI-Recruitment effect).
The SCAA and state-space models with independent NAA deviations had the lowest runtime. Estimating NAA deviations only for age-1, i.e. recruitment as random effects, broke the Hessian sparseness, making models m2, m3, m8, and m9 the slowest. Adding correlation structure to the NAA deviations increased runtime roughly 50% (comparing models m4 with m5-m7 and m10 with m11-m13).
All models except for m3 converged and successfully inverted the Hessian to produce SE estimates for (fixed effect) parameters. Inspection of the fixed effects parameter estimates shows that 2 of the logit transformed selectivity parameters are large implying selectivity of 1 for those ages. Fixing those parameters at 1 probably would correct this issue. WHAM stores information about hessian invertibility in mod$na_sdrep (should be FALSE), mod$sdrep$pdHess (should be TRUE). Also, mod$opt$convergence should generally be 0. See stats::nlminb() and TMB::sdreport() for details.
AIC for model m1 is not comparable with other models because comparing models in which parameters (here, recruitment deviations) are estimated as fixed effects versus random effects is messy and marginal AIC is not appropriate. Still, we include m1 to show 1) that WHAM can fit this NAA option, and 2) the poor retrospective pattern in the status quo assessment. Note that m2 is identical to m1 except that recruitment deviations are random effects instead of fixed effects. The retrospective patterns are very similar, but m2 takes about 3x longer to run.
# vign6_res[,11:13] = round(vign6_res[,11:13], 3)
# vign6_res$GSI_how = dplyr::recode(vign6_res$GSI_how, `0`='---',`2`='Limiting')
# posdef = which(vign6_res$pdHess == TRUE)
# thebest = which(vign6_res$dAIC < 2)
thebest = c(11,13)
vign6_res[1,"dAIC"] = '---'
vign6_res[1,"AIC"] = '---'
vign6_res %>%
dplyr::rename("Converged"="conv", "Pos def\nHessian"="pdHess", "Runtime\n(min)"="runtime", "$\\Delta AIC$"="dAIC",
"$\\rho_{R}$"="rho_R", "$\\rho_{SSB}$"="rho_SSB", "$\\rho_{\\overline{F}}$"="rho_Fbar") %>%
kable(escape = F) %>%
kable_styling(bootstrap_options = c("condensed","responsive")) %>%
# row_spec(posdef, background = gray.colors(10,end=0.95)[10]) %>%
row_spec(thebest, bold=TRUE)
Estimated NAA deviations
- All models estimated positive recruitment (age-1) deviations in the 1970s and 80s (red), and more negative deviations since 1990 (blue).
- Models with all numbers-at-age as random effects estimated less extreme recruitment deviations (lighter red and blue for age 1).
- Models with a GSI-Recruitment link also had less extreme recruitment deviations, because the GSI effect on expected recruitment accounted for some of this variability.
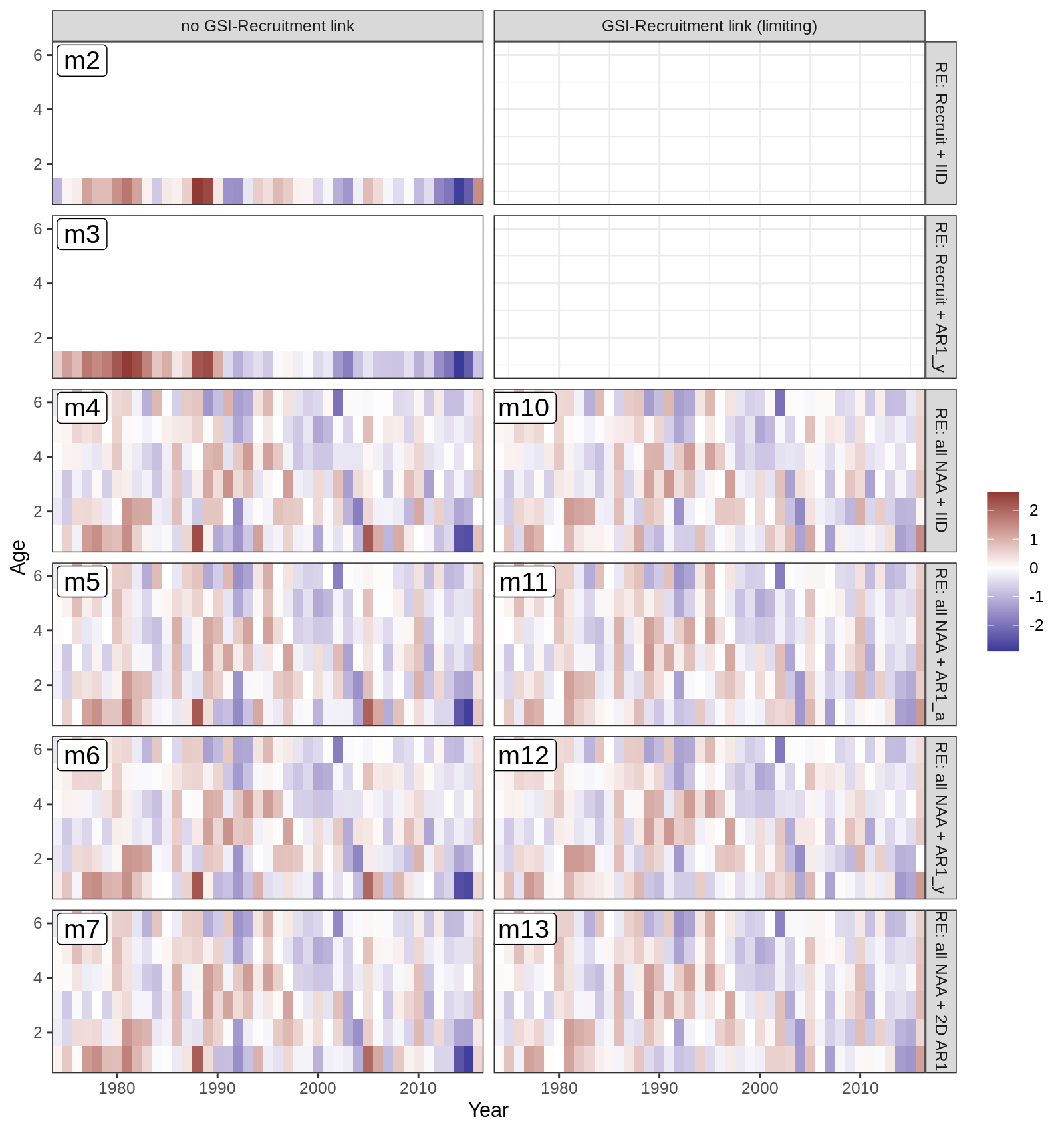
Estimated survival deviations by age (y-axis) and year (x-axis) for all converged models:
{ width=95% }
Retrospective patterns
The base model, m1 and all NAA_re$sigma = "rec" models (m2-m3 and m8-m9) had a severe retrospective pattern for recruitment, SSB, and $F$ (very high $\rho_R$). The full state-space model effectively alleviated this. Adding a GSI-Recruitment link to the state-space models further reduced $\rho_R$, but had negligible effects on $\rho_{SSB}$ and $\rho_{\overline{F}}$.
The AIC and Mohn's $\rho$ values were similar for m11 and m13, the models with lowest AIC.
The plots below compare retrospective patterns from the base model (m1, left) to those from the full model (m13, right).
Numbers-at-age, NAA
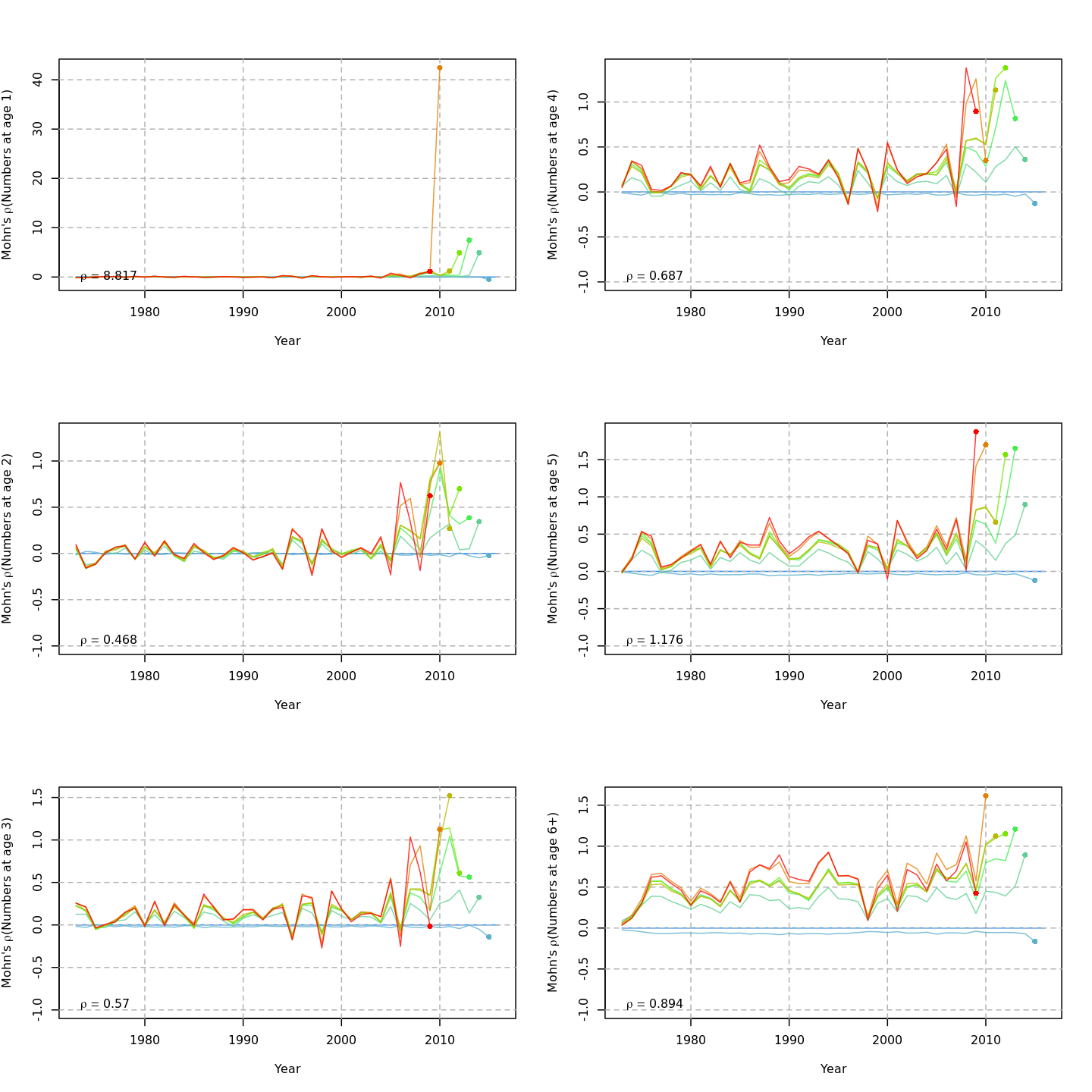{ width=45% }
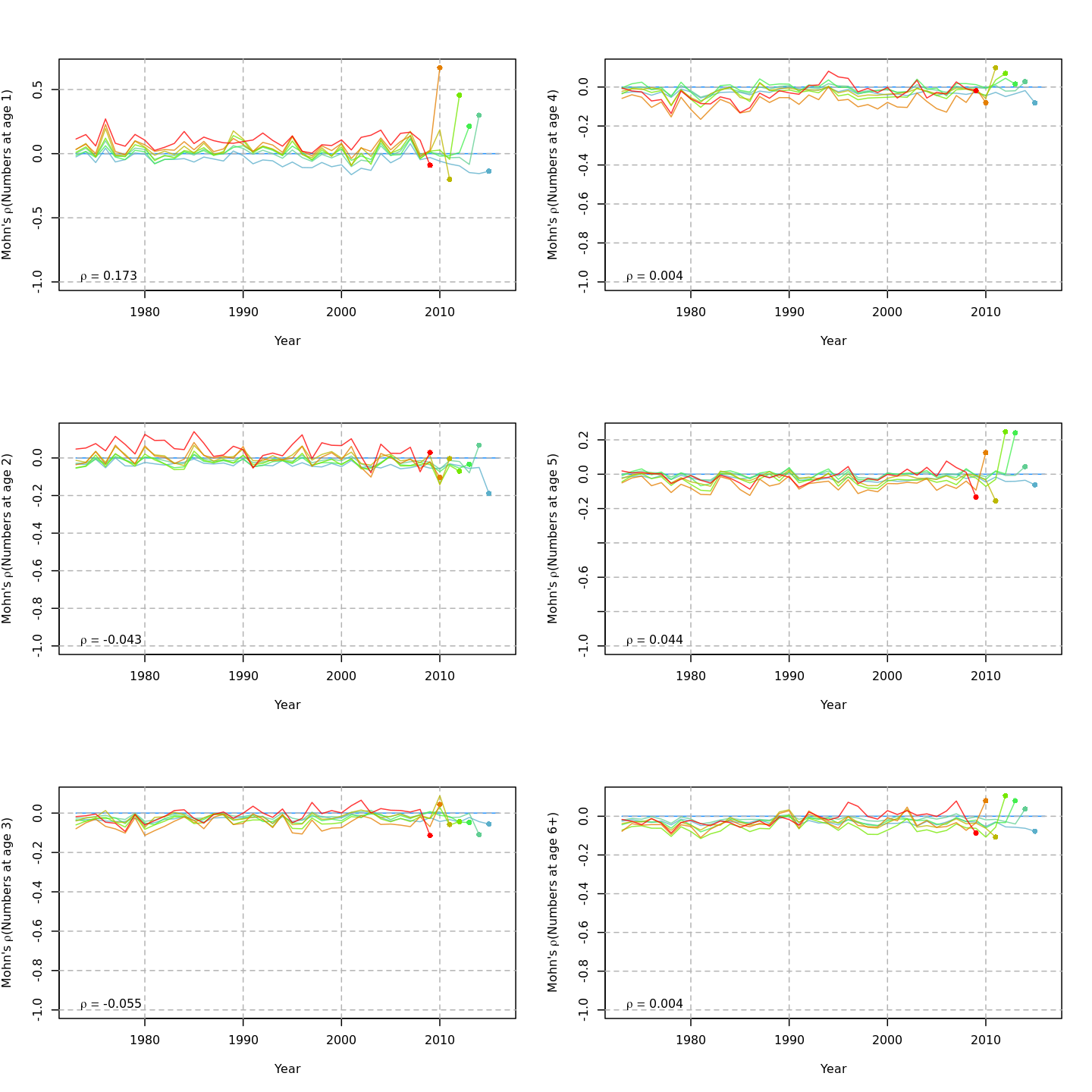{ width=45% }
Spawning stock biomass, SSB
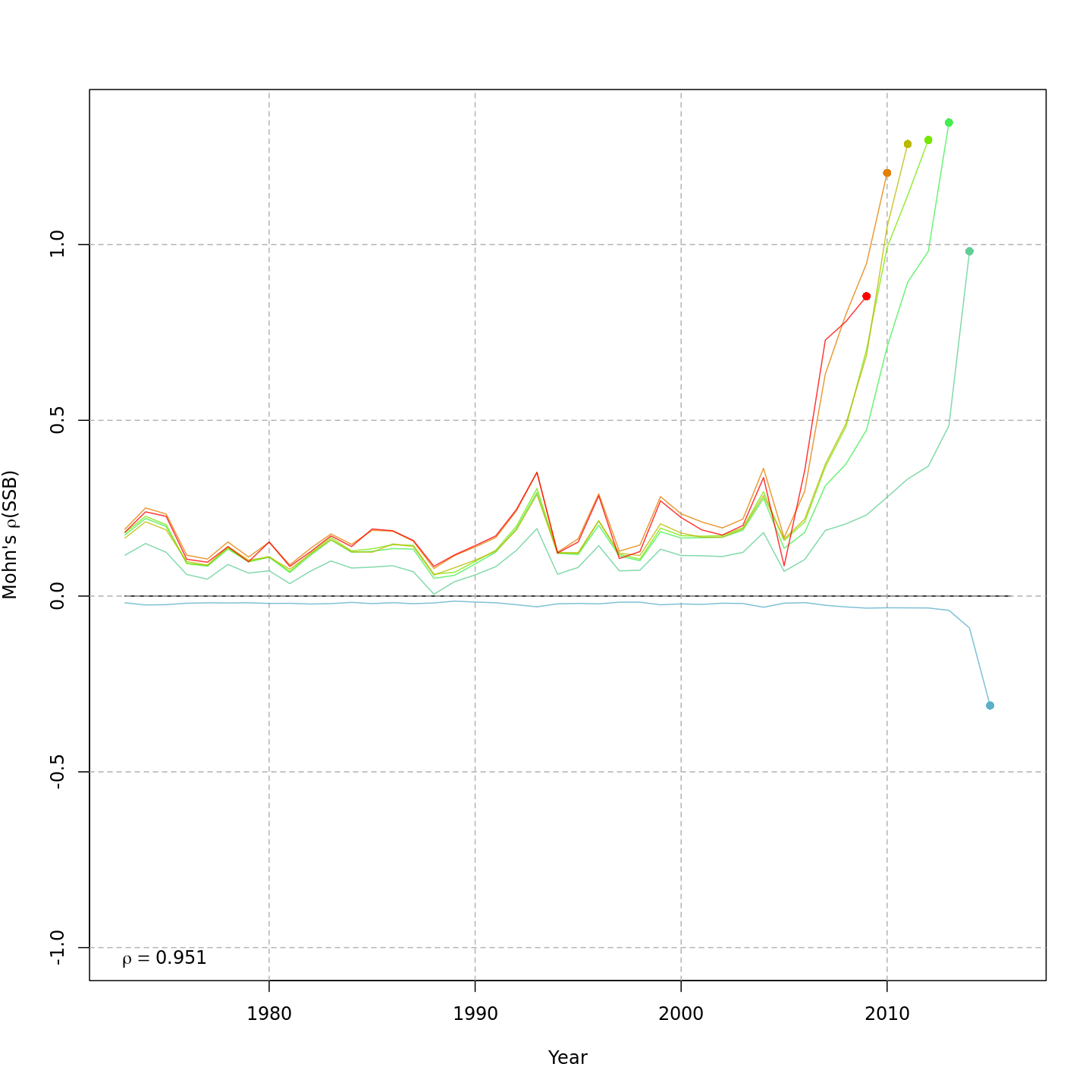{ width=45% }
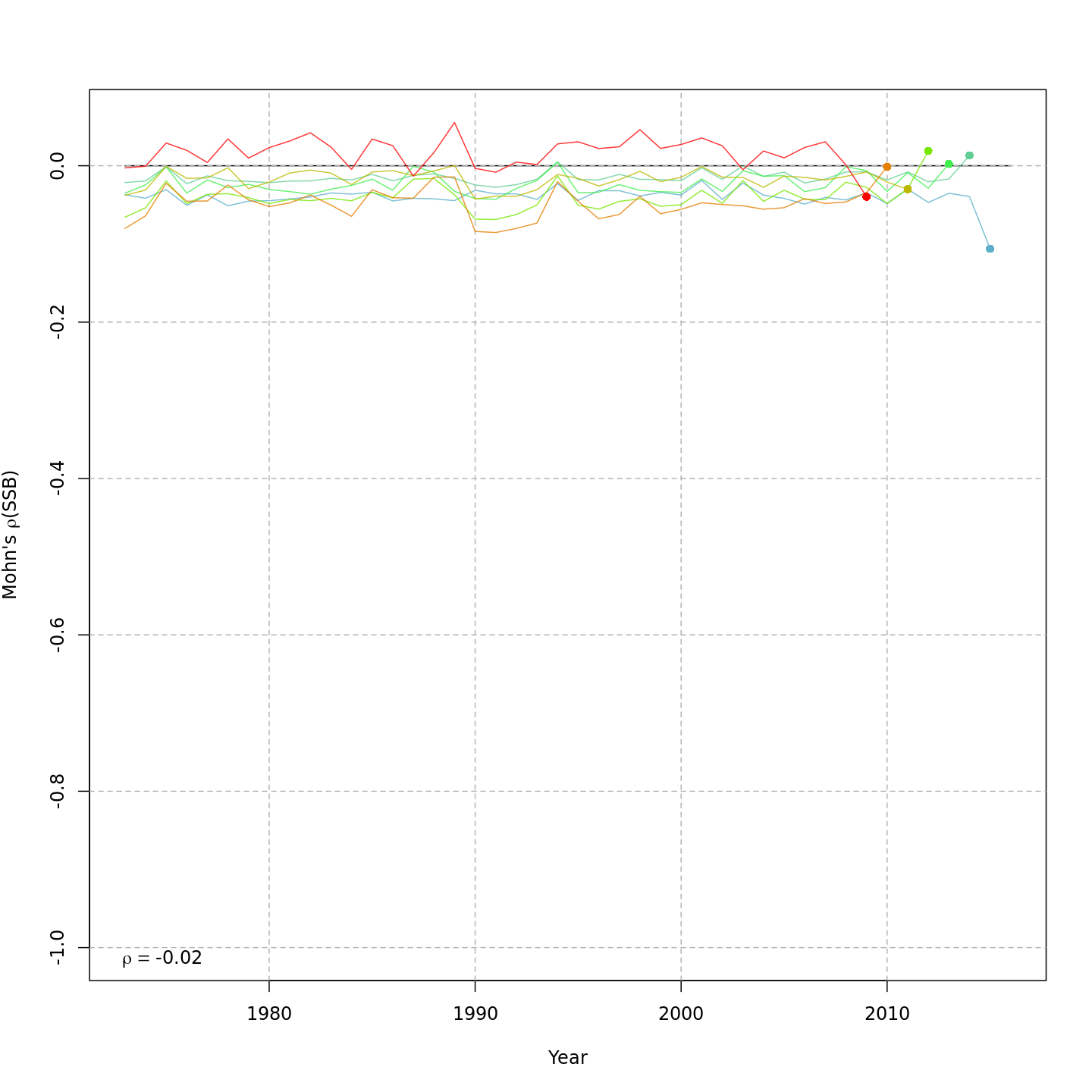{ width=45% }
Fishing mortality, F
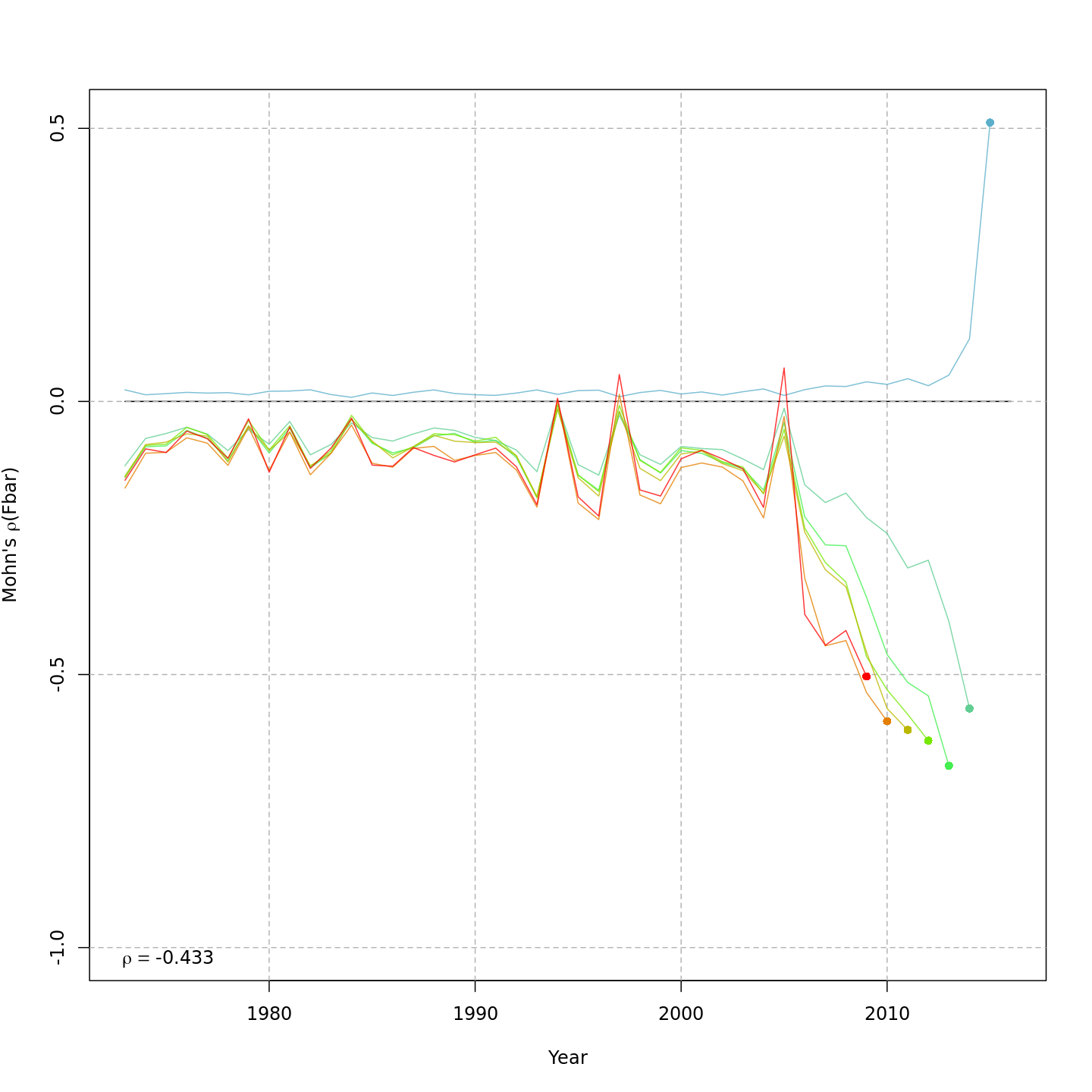{ width=45% }
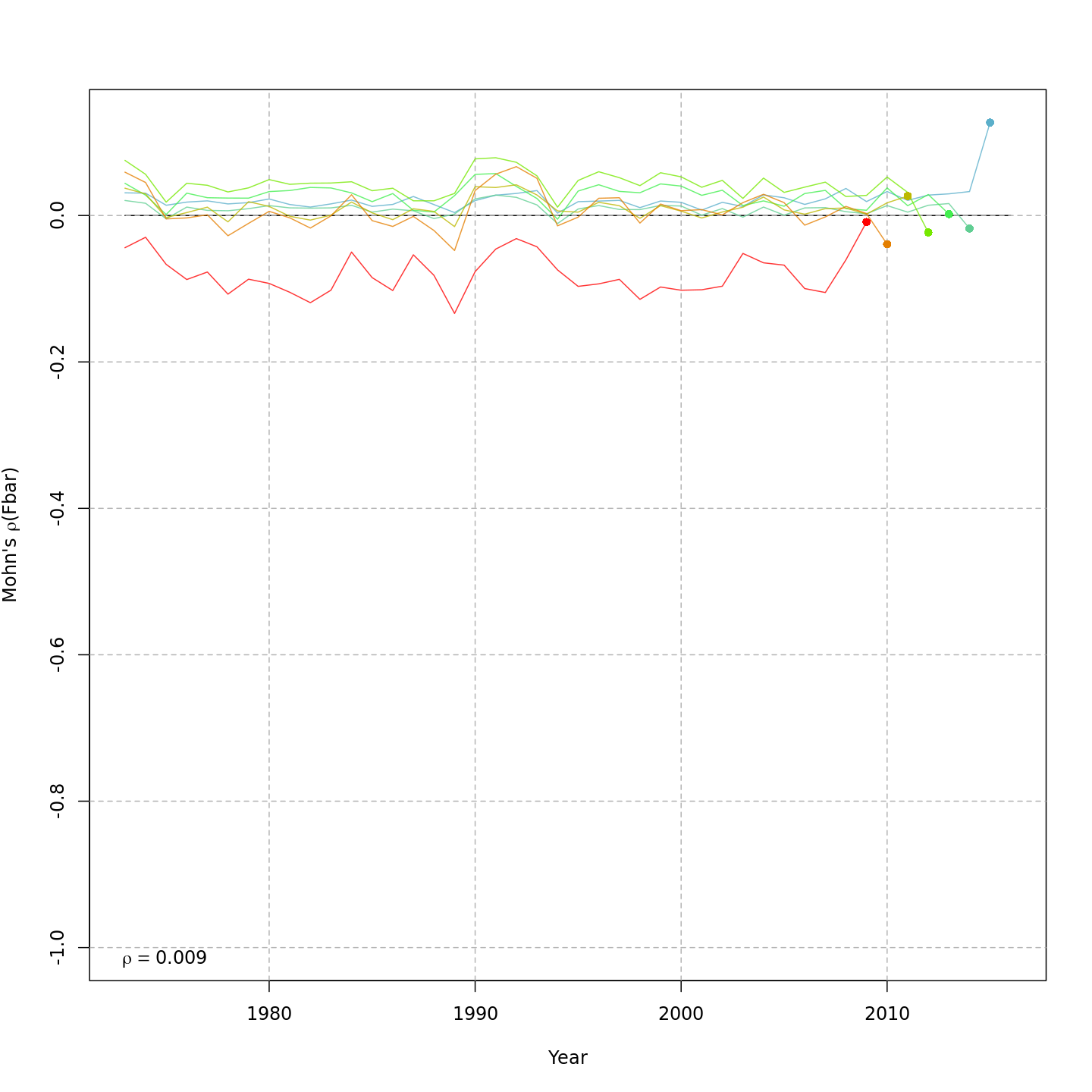{ width=45% }
Estimated GSI
Models with a GSI-Recruitment link estimated higher observation error and more smoothing of the GSI than those without. Compare the confidence intervals for m7 (left, no GSI-Recruitment link), to those for m13 (right, with GSI-Recruitment link).
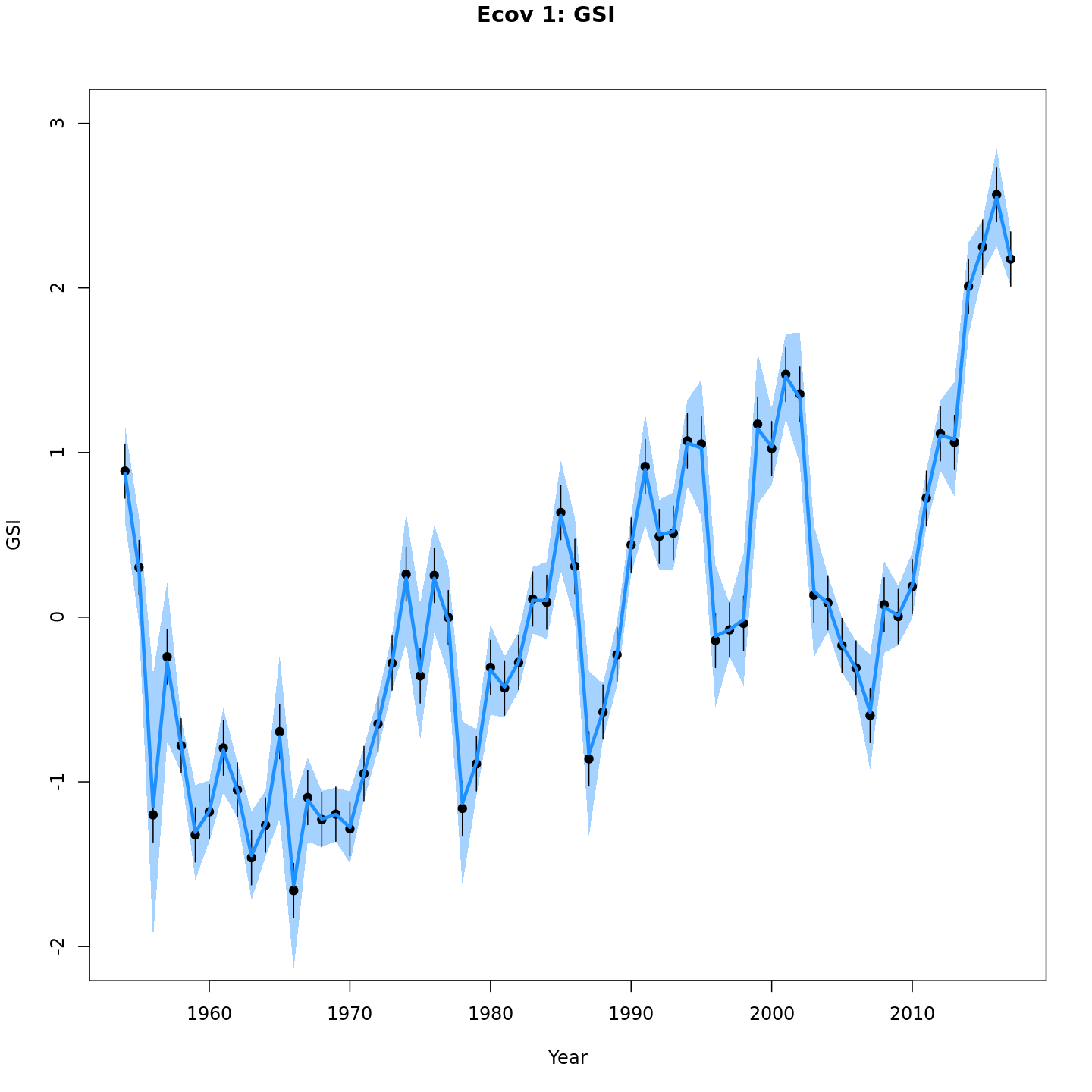{ width=45% }
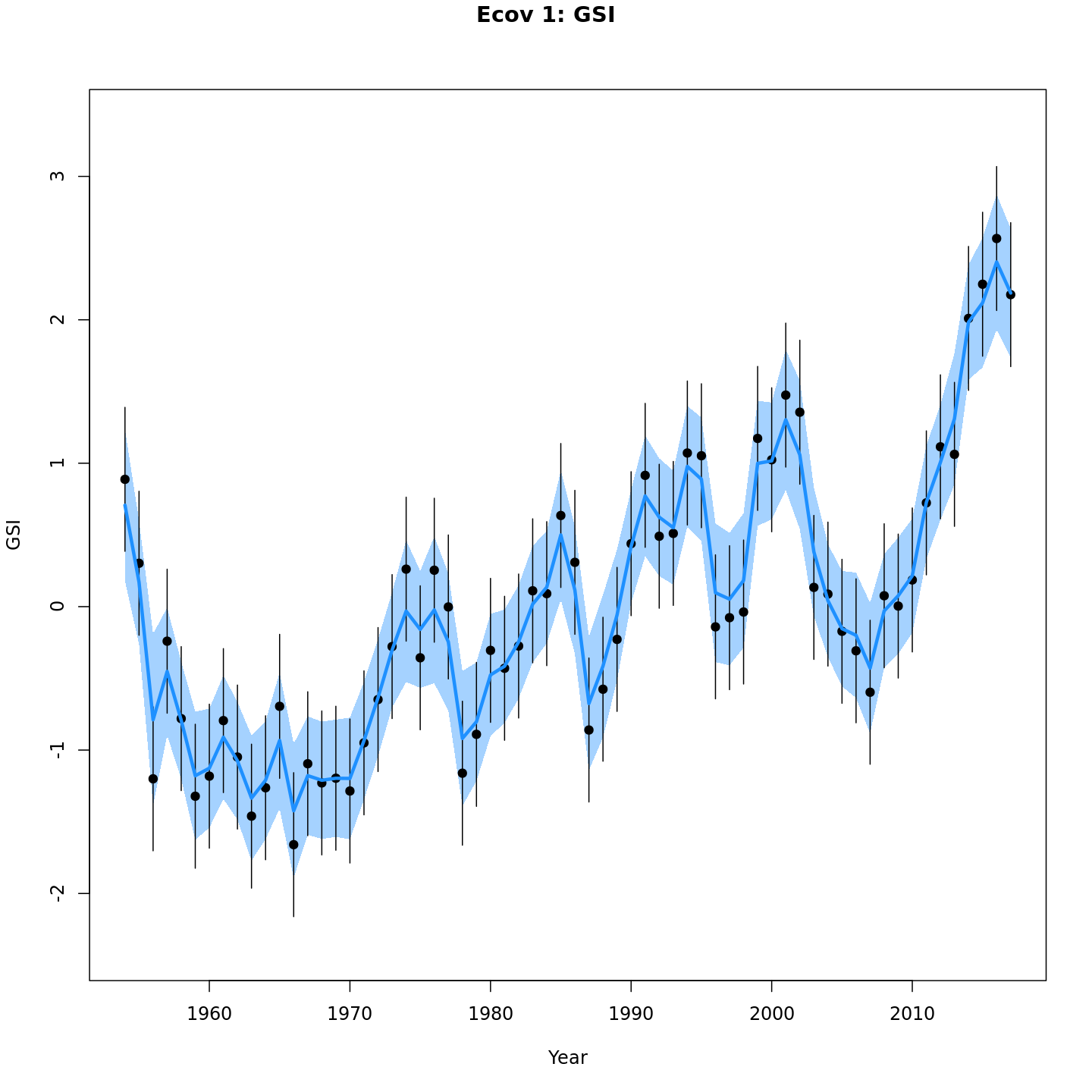{ width=45% }
Stock status
The state-space models, with or without the GSI-Recruitment link, estimated similar but slightly exaggerated trends in $SSB$ and $F$ compared to the base model. Left: $SSB$ and $F$ trends from the base model, m1. Right: $SSB$ and $F$ trends from the state-space model without GSI effect, m7.
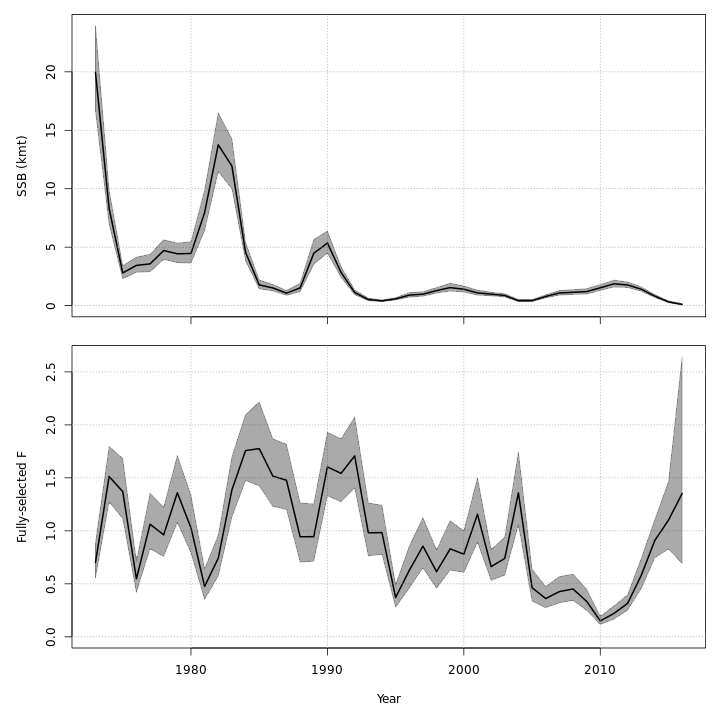{ width=45% }
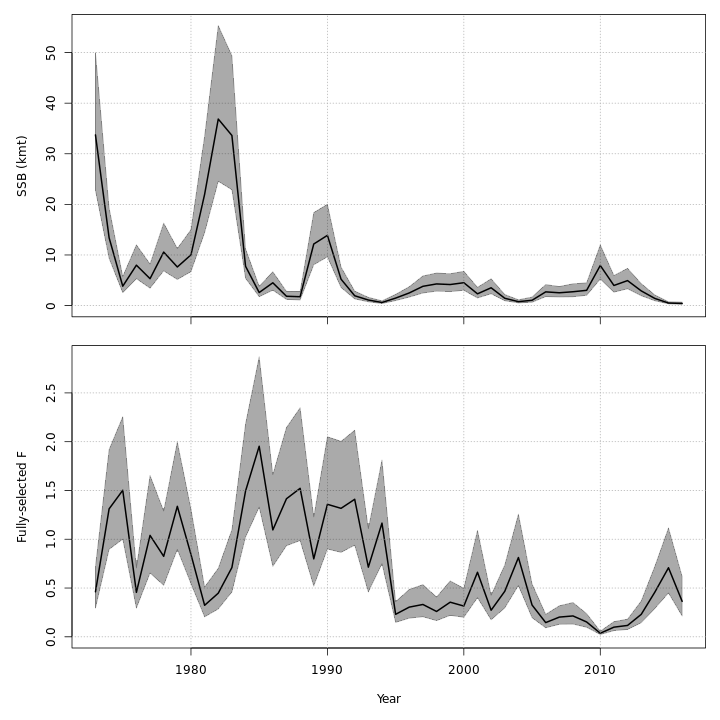{ width=45% }
Adding the GSI-Recruitment link to the state-space model did not impact the probability that the stock was overfished or experiencing overfishing in the final year, 2016 (m7 w/o GSI, left; m13 w/ GSI, right).
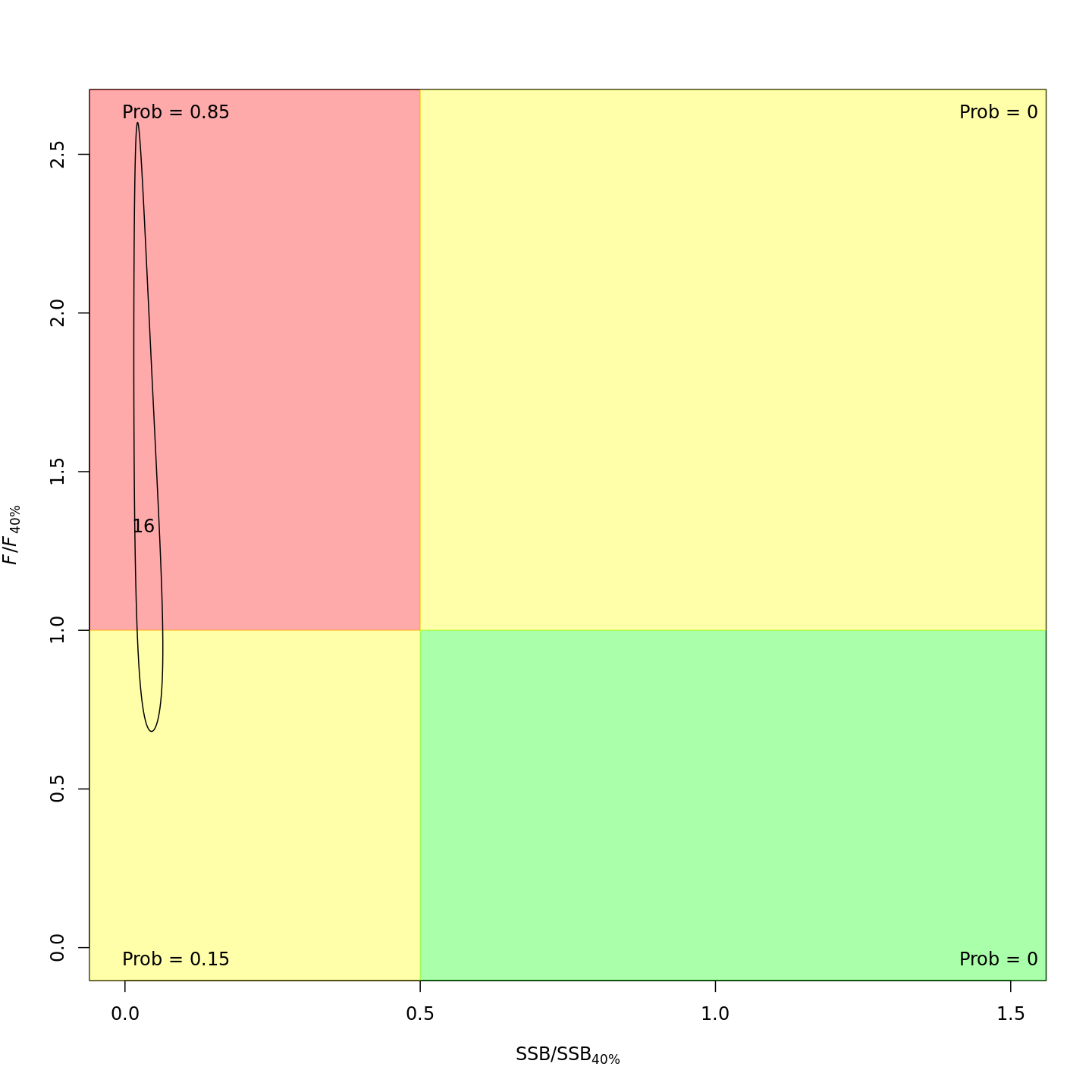{ width=45% }
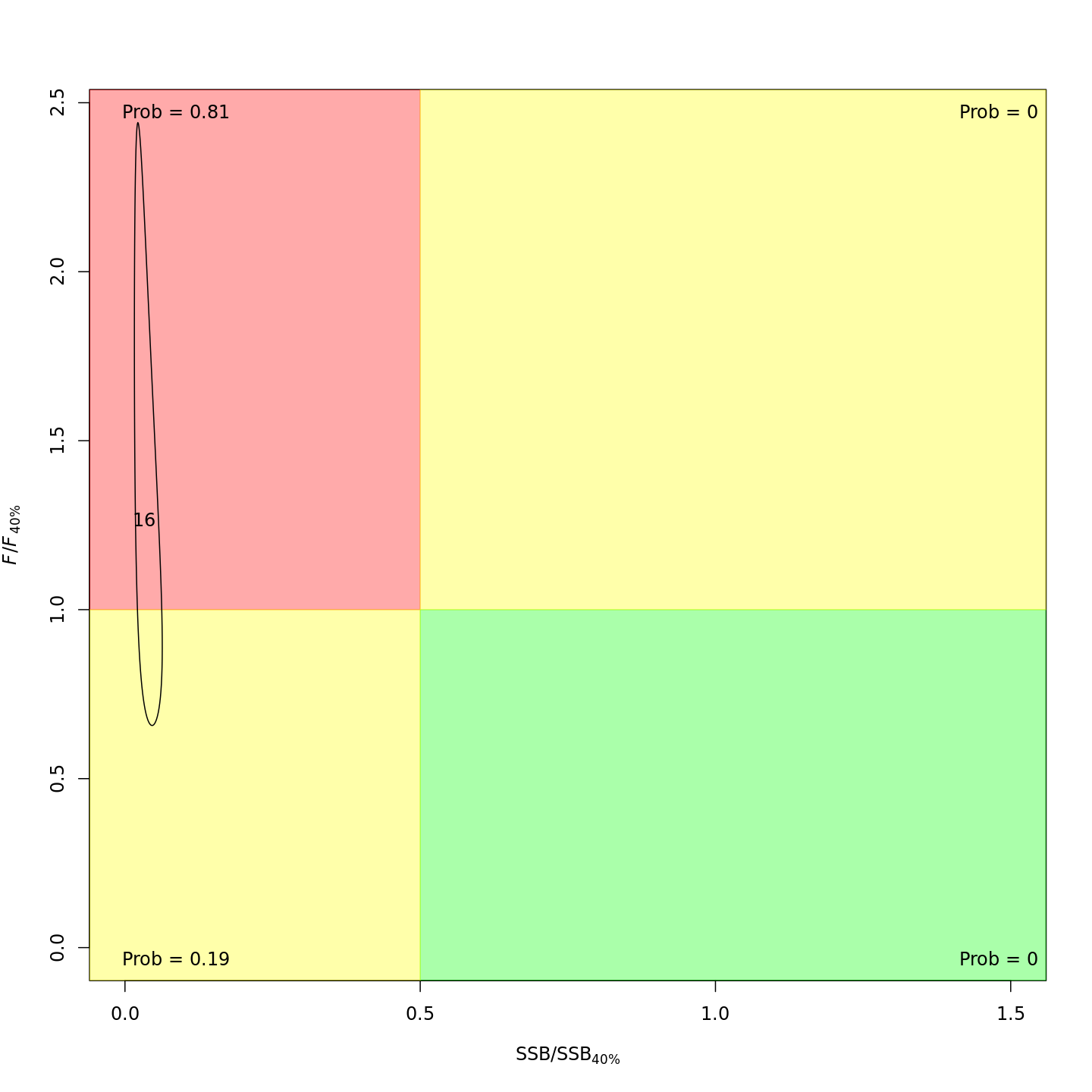{ width=45% }
timjmiller/wham documentation built on Feb. 4, 2025, 10:31 p.m.
R Package Documentation
Browse R Packages
We want your feedback!
Note that we can't provide technical support on individual packages. You should contact the package authors for that.
knitr::opts_chunk$set( collapse = TRUE, comment = "#>" ) # wham.dir <- find.package("wham") # knitr::opts_knit$set(root.dir = file.path(wham.dir,"extdata")) is.repo <- try(pkgload::load_all(compile=FALSE)) #this is needed to build the vignettes without the new version of wham installed. if(is.character(is.repo)) library(wham) #not building webpage #note that if plots are not yet pushed to the repo, they will not show up in the html. wham.dir <- find.package("wham") library(knitr) library(kableExtra)
In this vignette we walk through an example using the wham (WHAM = Woods Hole Assessment Model) package to run a state-space age-structured stock assessment model. WHAM is a generalization of code written for Miller et al. (2016) and Xu et al. (2018), and in this example we apply WHAM to the same stock, Southern New England / Mid-Atlantic Yellowtail Flounder.
This is the 6th WHAM example, which blends aspects from Ex 1, Ex 2, and Ex 5. We assume you already have wham installed. If not, see the Introduction. The simpler 1st example is available as a R script and vignette.
As in example 1:
- Stock: Southern New England-Mid Atlantic (SNEMA) yellowtail flounder
- Data: 1973-2011, 1 fishery and 2 indices
- Age compositions: logistic normal, treating observations of zero as missing (
age_comp = "logistic-normal-miss0") - Selectivity: age-specific
As in example 2:
- Beverton-Holt recruitment (
recruit_model = 3) - Environmental covariate (ecov) modeled as an AR1 process (
ecov$process_model = 'ar1') - Compare with and w/o ecov having a "limiting" (carrying capacity) effect on recruitment (
ecov$how = 2)
As in example 4:
- Age-specific selectivity with some ages fixed at 1 (fishery: 4-5, index1: 4, index2: 2-4)
As in example 5:
- Environmental covariate: Gulf Stream Index (GSI)
- 2D AR1 deviations by age and year (random effects)
Example 6 highlights WHAM's options for treating the yearly transitions in numbers-at-age (i.e. survival):
- Deterministic (as in statistical catch-at-age models, recruitment in each year estimated as independent fixed effect parameters)
- Recruitment deviations (from Bev-Holt expectation) are random effects
- independent
- AR1 deviations by year (autocorrelated)
- "Full state-space model" (survival of all ages are random effects)
- independent
- AR1 deviations by age
- AR1 deviations by year
- 2D AR1 deviations by age and year
1. Load data
Open R and load wham and other useful packages:
library(wham) library(tidyr) library(dplyr)
For a clean, runnable .R script, look at ex6_NAA.R in the example_scripts folder of the wham package.
You can run this entire example script with:
wham.dir <- find.package("wham") source(file.path(wham.dir, "example_scripts", "ex6_NAA.R"))
Let's create a directory for this analysis:
# choose a location to save output, otherwise will be saved in working directory write.dir <- "choose/where/to/save/output" # need to change e.g., tempdir(check=TRUE) dir.create(write.dir) setwd(write.dir)
We need the same ASAP data file as in example 1, and the environmental covariate (Gulf Stream Index, GSI).
Read in ex1_SNEMAYT.dat and GSI.csv:
asap3 <- read_asap3_dat(file.path(wham.dir,"extdata","ex2_SNEMAYT.dat")) env.dat <- read.csv(file.path(wham.dir,"extdata","GSI.csv"), header=T) head(env.dat)
As in example 5, the GSI data file does not have a standard error estimate, either for each yearly observation or one overall value. In such a case, WHAM can estimate the observation error for the environmental covariate, either as one overall value, $\sigma_{GSI}$, or yearly values as random effects, $\mathrm{log}\sigma_{{GSI}y} \sim \mathcal{N}(\mathrm{log}\sigma{GSI}, \sigma^2_{\sigma_{GSI}})$. In this example we choose the simpler option and estimate one observation error parameter, shared across years.
2. Specify models
Now we specify several models with different options for the numbers-at-age (NAA) transitions, i.e. survival:
df.mods <- data.frame(NAA_cor = c('---','iid','ar1_y','iid','ar1_a','ar1_y','2dar1','iid','ar1_y','iid','ar1_a','ar1_y','2dar1'), NAA_sigma = c('---',rep("rec",2),rep("rec+1",4),rep("rec",2),rep("rec+1",4)), R_how = paste0(c(rep("none",7),rep("limiting-lag-1-linear",6))), stringsAsFactors=FALSE) n.mods <- dim(df.mods)[1] df.mods$Model <- paste0("m",1:n.mods) df.mods <- df.mods %>% select(Model, everything()) # moves Model to first col
Look at the model table:
df.mods
3. Numbers-at-age options
To specify the options for modeling NAA transitions, include an optional list argument, NAA_re, to the prepare_wham_input function (see the prepare_wham_input help page). ASAP3 does not estimate random effects, and therefore these options are not specified in the ASAP data file. By default (NAA_re is NULL or not included), WHAM fits a traditional statistical catch-at-age model (NAA = predicted NAA for all ages, i.e. survival is deterministic). To fit a state-space model, we must specify NAA_re.
NAA_re is a list with the following entries:
$sigma: Which ages allow deviations from pred_NAA? Common options are specified with strings."rec": Recruitment deviations are random effects, survival of all other ages is deterministic"rec+1": Survival of all ages is stochastic ("full state space model"), with 2 estimated $\sigma_a$, one for recruitment and one shared among other ages$cor: Correlation structure for the NAA deviations. Options are:"iid": NAA deviations vary by year and age, but uncorrelated."ar1_a": NAA deviations correlated by age (AR1)."ar1_y": NAA deviations correlated by year (AR1)."2dar1": NAA deviations correlated by year and age (2D AR1, as for $M$ in example 5).
Alternatively, you can specify a more complex configuration of sigma parameter estimation via NAA_re$sigma_map as an array (n_stocks x n_regions x n_ages) of integers (and NAs to fix parameters). For example (with 1 stock and 1 region here), NAA_re$sigma = array(c(1,2,2,3,3,3), dim = c(1,1,6)) will estimate three $\sigma$ parameters, with recruitment (age-1) deviations having their own $\sigma_R$, ages 2-3 sharing $\sigma_2$, and ages 4-6 sharing $\sigma_3$.
To fit model m1 (SCAA) we do not have to supply anything:
NAA_re <- NULL # or simply leave out of call to prepare_wham_input
To fit model m3, recruitment deviations are correlated random effects:
NAA_re <- list(sigma="rec", cor="ar1_y")
And to fit model m7, numbers at all ages are random effects correlated by year AND age:
NAA_re <- list(sigma="rec+1", cor="2dar1")
4. Linking recruitment to an environmental covariate (GSI)
As described in example 2, the environmental covariate options are fed to prepare_wham_input as a list, ecov. This example differs from example 2 in that:
ecov$logsigma = "est_1"estimates the GSI observation error ($\sigma_{GSI}$, one overall value for all years like in example 5). The other option is"est_re"to allow the GSI observation error to have yearly fluctuations (random effects). The Cold Pool Index in example 2 had yearly observation errors given, so this was not necessary.ecov$R_how = matrix("none",1,1)orecov$R_how = NULLestimates the GSI time-series model (AR1) for models without a GSI-Recruitment effect, in order to compare AIC with models that do include the effect. Settingecov$R_how = matrix("limiting-lag-1-linear,1,1)specifies that the GSI iyear $t$ affects the Beverton-Holt $\beta$ parameter ("limiting" / carrying capacity effect) in year $t+1$ linearly (on log scale).
For example, the ecov list for models m8-m13 with the linear GSI-$\beta$ effect:
ecov <- list( label = "GSI", mean = as.matrix(env.dat$GSI), logsigma = 'est_1', # estimate obs sigma, 1 value shared across years year = env.dat$year, use_obs = matrix(1, ncol=1, nrow=dim(env.dat)[1]), # use all obs (=1) process_model = 'ar1', # "rw" or "ar1" R_how = matrix("limiting-lag-1-linear",1,1)) # n_Ecov x n_stocks x n_ages x n_regions
Note that you can set ecov = NULL to fit the model without environmental covariate data, but here we fit the ecov data even for models without the GSI effect on recruitment (m1-m7) so that we can compare them via AIC (need to have the same data in the likelihood). We accomplish this by setting ecov$R_how = matrix("none",1,1) and ecov$process_model = "ar1".
5. Run all models
All models use the same options for expected recruitment (Beverton-Holt stock-recruit function) and selectivity (age-specific, with one or two ages fixed at 1). We specify recruitment decoupling only for consistency with the original implicit assumption in WHAM.
mods <- vector("list",n.mods) for(m in 1:n.mods){ NAA_list <- list(cor=df.mods[m,"NAA_cor"], sigma=df.mods[m,"NAA_sigma"], decouple_recruitment = FALSE) if(NAA_list$sigma == '---') NAA_list = NULL ecov <- list( label = "GSI", mean = as.matrix(env.dat$GSI), logsigma = 'est_1', # estimate obs sigma, 1 value shared across years year = env.dat$year, use_obs = matrix(1, ncol=1, nrow=dim(env.dat)[1]), # use all obs (=1) process_model = 'ar1', # "rw" or "ar1" recruitment_how = matrix(df.mods$R_how[m])) # n_Ecov x n_stocks input <- suppressWarnings(prepare_wham_input(asap3, recruit_model = 3, # Bev Holt recruitment model_name = "Ex 6: Numbers-at-age", selectivity=list(model=rep("age-specific",3), re=c("none","none","none"), initial_pars=list(c(0.1,0.5,0.5,1,1,1),c(0.5,0.5,0.5,1,0.5,0.5),c(0.5,0.5,1,1,1,1)), fix_pars=list(4:6,4,3:6)), NAA_re = NAA_list, ecov=ecov, age_comp = "logistic-normal-miss0")) # logistic normal, treat 0 obs as missing # Fit model mods[[m]] <- fit_wham(input, do.retro=T, do.osa=F) # Save model saveRDS(mods[[m]], file=paste0(df.mods$Model[m],".rds")) # If desired, do projections # mod_proj <- project_wham(mod) # saveRDS(mod_proj, file=paste0(df.mods$Model[m],"_proj.rds")) }
6. Compare models
#data(vign6_res) #not needed
Get model convergence and stats.
opt_conv = 1-sapply(mods, function(x) x$opt$convergence) ok_sdrep = sapply(mods, function(x) if(x$na_sdrep==FALSE & !is.na(x$na_sdrep)) 1 else 0) df.mods$conv <- as.logical(opt_conv) df.mods$pdHess <- as.logical(ok_sdrep)
Only calculate AIC and Mohn's rho for converged models.
df.mods$runtime <- sapply(mods, function(x) x$runtime) df.mods$NLL <- sapply(mods, function(x) round(x$opt$objective,3)) not_conv <- !df.mods$conv | !df.mods$pdHess mods2 <- mods mods2[not_conv] <- NULL df.aic.tmp <- as.data.frame(compare_wham_models(mods2, table.opts=list(sort=FALSE, calc.rho=TRUE))$tab) df.aic <- df.aic.tmp[FALSE,] ct = 1 for(i in 1:n.mods){ if(not_conv[i]){ df.aic[i,] <- rep(NA,5) } else { df.aic[i,] <- df.aic.tmp[ct,] ct <- ct + 1 } } df.aic[,1:2] <- format(round(df.aic[,1:2], 1), nsmall=1) df.aic[,3:5] <- format(round(df.aic[,3:5], 3), nsmall=3) df.aic[grep("NA",df.aic$dAIC),] <- "---" df.mods <- cbind(df.mods, df.aic) rownames(df.mods) <- NULL
Look at results table.
df.mods
vign6_res
Save results table.
write.csv(df.mods, file="ex6_table.csv",quote=F, row.names=F)
Plot output for models that converged.
mods[[1]]$env$data$recruit_model = 2 # m1 (SCAA) didn't actually fit a Bev-Holt for(m in which(!not_conv)){ plot_wham_output(mod=mods[[m]], dir.main=file.path(getwd(),paste0("m",m))) #html by default }
7. Results
Two models had very similar AIC and were overwhelmingly supported relative to the other models (bold in table below): m11 (all NAA are random effects with correlation by age, GSI-Recruitment effect) and m13 (all NAA are random effects with correlation by age and year, GSI-Recruitment effect).
The SCAA and state-space models with independent NAA deviations had the lowest runtime. Estimating NAA deviations only for age-1, i.e. recruitment as random effects, broke the Hessian sparseness, making models m2, m3, m8, and m9 the slowest. Adding correlation structure to the NAA deviations increased runtime roughly 50% (comparing models m4 with m5-m7 and m10 with m11-m13).
All models except for m3 converged and successfully inverted the Hessian to produce SE estimates for (fixed effect) parameters. Inspection of the fixed effects parameter estimates shows that 2 of the logit transformed selectivity parameters are large implying selectivity of 1 for those ages. Fixing those parameters at 1 probably would correct this issue. WHAM stores information about hessian invertibility in mod$na_sdrep (should be FALSE), mod$sdrep$pdHess (should be TRUE). Also, mod$opt$convergence should generally be 0. See stats::nlminb() and TMB::sdreport() for details.
AIC for model m1 is not comparable with other models because comparing models in which parameters (here, recruitment deviations) are estimated as fixed effects versus random effects is messy and marginal AIC is not appropriate. Still, we include m1 to show 1) that WHAM can fit this NAA option, and 2) the poor retrospective pattern in the status quo assessment. Note that m2 is identical to m1 except that recruitment deviations are random effects instead of fixed effects. The retrospective patterns are very similar, but m2 takes about 3x longer to run.
# vign6_res[,11:13] = round(vign6_res[,11:13], 3) # vign6_res$GSI_how = dplyr::recode(vign6_res$GSI_how, `0`='---',`2`='Limiting') # posdef = which(vign6_res$pdHess == TRUE) # thebest = which(vign6_res$dAIC < 2) thebest = c(11,13) vign6_res[1,"dAIC"] = '---' vign6_res[1,"AIC"] = '---' vign6_res %>% dplyr::rename("Converged"="conv", "Pos def\nHessian"="pdHess", "Runtime\n(min)"="runtime", "$\\Delta AIC$"="dAIC", "$\\rho_{R}$"="rho_R", "$\\rho_{SSB}$"="rho_SSB", "$\\rho_{\\overline{F}}$"="rho_Fbar") %>% kable(escape = F) %>% kable_styling(bootstrap_options = c("condensed","responsive")) %>% # row_spec(posdef, background = gray.colors(10,end=0.95)[10]) %>% row_spec(thebest, bold=TRUE)
Estimated NAA deviations
- All models estimated positive recruitment (age-1) deviations in the 1970s and 80s (red), and more negative deviations since 1990 (blue).
- Models with all numbers-at-age as random effects estimated less extreme recruitment deviations (lighter red and blue for age 1).
- Models with a GSI-Recruitment link also had less extreme recruitment deviations, because the GSI effect on expected recruitment accounted for some of this variability.
Estimated survival deviations by age (y-axis) and year (x-axis) for all converged models:
{ width=95% }
Retrospective patterns
The base model, m1 and all NAA_re$sigma = "rec" models (m2-m3 and m8-m9) had a severe retrospective pattern for recruitment, SSB, and $F$ (very high $\rho_R$). The full state-space model effectively alleviated this. Adding a GSI-Recruitment link to the state-space models further reduced $\rho_R$, but had negligible effects on $\rho_{SSB}$ and $\rho_{\overline{F}}$.
The AIC and Mohn's $\rho$ values were similar for m11 and m13, the models with lowest AIC.
The plots below compare retrospective patterns from the base model (m1, left) to those from the full model (m13, right).
Numbers-at-age, NAA
{ width=45% }{ width=45% }
Spawning stock biomass, SSB
{ width=45% }{ width=45% }
Fishing mortality, F
{ width=45% }{ width=45% }
Estimated GSI
Models with a GSI-Recruitment link estimated higher observation error and more smoothing of the GSI than those without. Compare the confidence intervals for m7 (left, no GSI-Recruitment link), to those for m13 (right, with GSI-Recruitment link).
{ width=45% }{ width=45% }
Stock status
The state-space models, with or without the GSI-Recruitment link, estimated similar but slightly exaggerated trends in $SSB$ and $F$ compared to the base model. Left: $SSB$ and $F$ trends from the base model, m1. Right: $SSB$ and $F$ trends from the state-space model without GSI effect, m7.
{ width=45% }{ width=45% }
Adding the GSI-Recruitment link to the state-space model did not impact the probability that the stock was overfished or experiencing overfishing in the final year, 2016 (m7 w/o GSI, left; m13 w/ GSI, right).
{ width=45% }{ width=45% }
R Package Documentation
Browse R Packages
We want your feedback!
Note that we can't provide technical support on individual packages. You should contact the package authors for that.
Embedding an R snippet on your website
Add the following code to your website.
For more information on customizing the embed code, read Embedding Snippets.