README.md

In stokes: The Exterior Calculus

The stokes package: exterior calculus in R

Overview

The stokes package provides functionality for working with the exterior calculus. It includes tensor products and wedge products and a variety of use-cases. The canonical reference would be Spivak (see references). A detailed vignette is provided in the package.

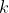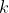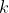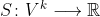The package deals with -tensors and -forms. A -tensor is a multilinear map , where 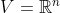is considered as a vector space. Given two 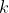-tensors 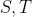the package can calculate their outer product 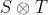using natural R idiom (see below and the vignette for details).

A 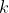-form is an alternating 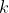-tensor, that is a 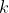-tensor 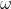with the property that linear dependence of 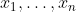implies that 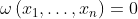. Given 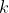-forms 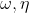, the package provides R idiom for calculating their wedge product .

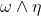Installation

You can install the released version of stokes from CRAN with:

# install.packages("stokes")  # uncomment this to install the package
library("stokes")
set.seed(0)

The stokes package in use

The package has two main classes of objects, kform and ktensor. In the package, we can create a 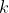-tensor by supplying function as.ktensor() a matrix of indices and a vector of coefficients, for example:

jj <- as.ktensor(rbind(1:3,2:4),1:2)
jj
#> A linear map from V^3 to R with V=R^4:
#>            val
#>  2 3 4  =    2
#>  1 2 3  =    1

Above, object jj is equal to (see Spivak, p76 for details).

We can coerce tensors to a function and then evaluate it:

KT <- as.ktensor(cbind(1:4,2:5),1:4)
f <- as.function(KT)
E <- matrix(rnorm(10),5,2)
f(E)
#> [1] 11.23556

Tensor products are implemented:

KT %X% KT
#> A linear map from V^4 to R with V=R^5:
#>              val
#>  1 2 1 2  =    1
#>  2 3 1 2  =    2
#>  3 4 3 4  =    9
#>  2 3 4 5  =    8
#>  1 2 2 3  =    2
#>  1 2 4 5  =    4
#>  4 5 4 5  =   16
#>  2 3 3 4  =    6
#>  4 5 3 4  =   12
#>  1 2 3 4  =    3
#>  3 4 4 5  =   12
#>  3 4 2 3  =    6
#>  4 5 2 3  =    8
#>  3 4 1 2  =    3
#>  2 3 2 3  =    4
#>  4 5 1 2  =    4

Above we see .

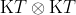Alternating forms

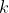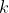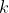An alternating form (or -form) is an antisymmetric -tensor; the package can convert a general -tensor to alternating form using the Alt() function:

Alt(KT)
#> A linear map from V^2 to R with V=R^5:
#>           val
#>  5 4  =  -2.0
#>  4 5  =   2.0
#>  4 3  =  -1.5
#>  3 2  =  -1.0
#>  2 3  =   1.0
#>  3 4  =   1.5
#>  2 1  =  -0.5
#>  1 2  =   0.5

However, the package provides a bespoke and efficient representation for 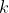-forms as objects with class kform. Such objects may be created using the as.kform() function:

M <- matrix(c(4,2,3,1,2,4),2,3,byrow=TRUE)
M
#>      [,1] [,2] [,3]
#> [1,]    4    2    3
#> [2,]    1    2    4
KF <- as.kform(M,c(1,5))
KF
#> An alternating linear map from V^3 to R with V=R^4:
#>            val
#>  1 2 4  =    5
#>  2 3 4  =    1

Above, we see that KF is equal to . We may coerce KF to functional form:

f <- as.function(KF)
E <- matrix(rnorm(12),4,3)
f(E)
#> [1] -5.979544

Above, we evaluate KF at a point in 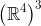[the three columns of matrix E are each interpreted as vectors in ].

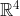The wedge product

The wedge product of two 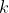-forms is implemented as ^ or wedge():

KF2 <- kform_general(6:9,2,1:6)
KF2
#> An alternating linear map from V^2 to R with V=R^9:
#>          val
#>  8 9  =    6
#>  7 9  =    5
#>  6 9  =    4
#>  7 8  =    3
#>  6 8  =    2
#>  6 7  =    1
KF ^ KF2
#> An alternating linear map from V^5 to R with V=R^9:
#>                val
#>  1 2 4 6 7  =    5
#>  1 2 4 6 8  =   10
#>  2 3 4 6 8  =    2
#>  2 3 4 7 8  =    3
#>  2 3 4 6 9  =    4
#>  1 2 4 6 9  =   20
#>  2 3 4 6 7  =    1
#>  2 3 4 7 9  =    5
#>  1 2 4 7 8  =   15
#>  2 3 4 8 9  =    6
#>  1 2 4 7 9  =   25
#>  1 2 4 8 9  =   30

The package can accommodate a number of results from the exterior calculus such as elementary forms:

dx <- as.kform(1)
dy <- as.kform(2)
dz <- as.kform(3)
dx ^ dy ^ dz  # element of volume 
#> An alternating linear map from V^3 to R with V=R^3:
#>            val
#>  1 2 3  =    1

A number of useful functions from the exterior calculus are provided, such as the gradient of a scalar function:

grad(1:6)
#> An alternating linear map from V^1 to R with V=R^6:
#>        val
#>  6  =    6
#>  5  =    5
#>  4  =    4
#>  3  =    3
#>  2  =    2
#>  1  =    1

The package takes the leg-work out of the exterior calculus:

grad(1:4) ^ grad(1:6)
#> An alternating linear map from V^2 to R with V=R^6:
#>          val
#>  4 5  =   20
#>  1 5  =    5
#>  2 5  =   10
#>  3 5  =   15
#>  2 6  =   12
#>  4 6  =   24
#>  3 6  =   18
#>  1 6  =    6

References

The most concise reference is

• Spivak 1971. Calculus on manifolds, Addison-Wesley.

But a more leisurely book would be

• Hubbard and Hubbard 2015. Vector calculus, linear algebra, and differential forms: a unified approach. Matrix Editions

Further information

For more detail, see the package vignette

vignette("stokes")

stokes documentation built on June 22, 2024, 11:56 a.m.